Chapter 1.3, Problem 3PSA

a.

To determine

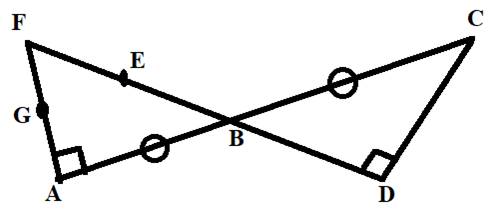
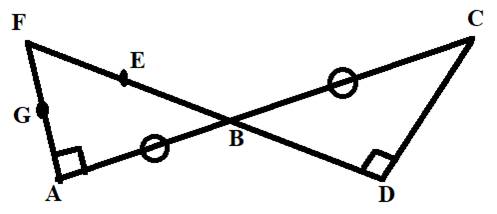
To Find: All points collinear with E and F .

Answer to Problem 3PSA

B and D are points collinear with E and F .

Explanation of Solution

Given:

  

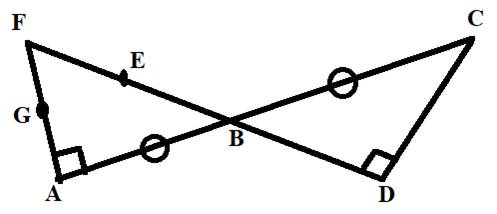
Concept Used:

Three or more points are said to be collinear if they lies on the same straight line.

Calculation:

Here, we points B and D are points collinear with E and F .

Conclusion:

B and D are points collinear with E and F .

b.

To determine

To Find: Whether points G, E and D are collinear? Whether points F and C are collinear?

Answer to Problem 3PSA

No, points G, E and D are non-collinear. Also, points F and C are non-collinear.

Explanation of Solution

Given:

  

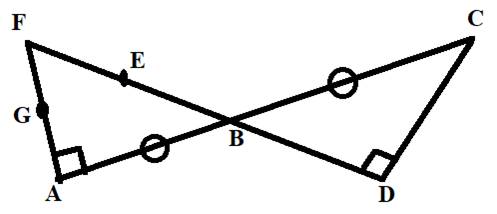
Concept Used:

Three or more points are said to be collinear if they lies on the same straight line.

Calculation:

Here, we points G, E and D are not on the same straight line, hence these points are non-collinear. Also, points F and C are not on the same straight line, hence these points are non-collinear.

Conclusion:

Points G, E and D are non-collinear. Also, points F and C are non-collinear.

c.

To determine

To Find: Which two segments are congruent?

Answer to Problem 3PSA

  $\overline{AB}\cong \overline{BC}$

Explanation of Solution

Given:

  

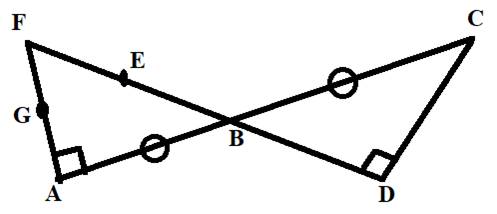
Concept Used:

Two or more line segments are said to be congruent if they are of the same measure.

Calculation:

Here, line segments AB and BC are labeled with tick marks, i.e., these line segments are of the same length.

  $\begin{array}{l}\Rightarrow l\left(\overline{AB}\right)=l\left(\overline{BC}\right)\\ \Rightarrow \overline{AB}\cong \overline{BC}\end{array}$

Conclusion:

  $\overline{AB}\cong \overline{BC}$

d.

To determine

To Find: Whether $\angle A\cong \angle D$ ?

Answer to Problem 3PSA

Yes, $\angle A\cong \angle D$

Explanation of Solution

Given:

  

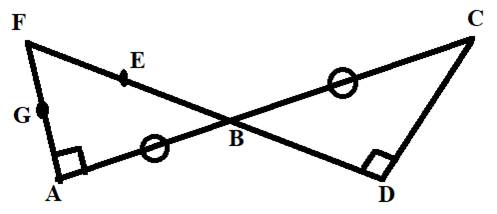
Concept Used:

Two or more angles are said to be congruent if they are of the same measure.

Calculation:

Here, we have

  $\begin{array}{l}\because \angle FAB\text{ and }\angle BDC\text{are right angles}\\ \Rightarrow m\angle FAB=90°\&m\angle BDC=90°\\ \Rightarrow m\angle FAB=m\angle BDC=90°\\ \Rightarrow \angle FAB\cong \angle BDC\\ \Rightarrow \angle A\cong \angle D\end{array}$

Conclusion:

  $\angle A\cong \angle D$

e.

To determine

To Find: Whether $\angle F\cong \angle ABF$ ?

Answer to Problem 3PSA

No, $\angle F\cong \angle ABF$

Explanation of Solution

Given:

  

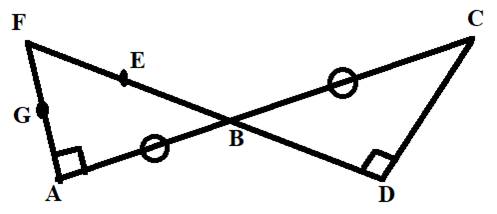
Concept Used:

Two or more angles are said to be congruent if they are of the same measure. Angles opposite to arms of equal length are equal in measure.

Calculation:

Since, it is not mention that sides AF and AB are of equal measure.

  $\begin{array}{l}\Rightarrow m\angle F\ne m\angle ABF\\ \Rightarrow \angle F\cancel{\cong }\angle ABF\end{array}$

Conclusion:

  $\angle F\cancel{\cong }\angle ABF$

f.

To determine

To Find: Where does the lines AC and FE intersects?

Answer to Problem 3PSA

Point B

Explanation of Solution

Given:

  

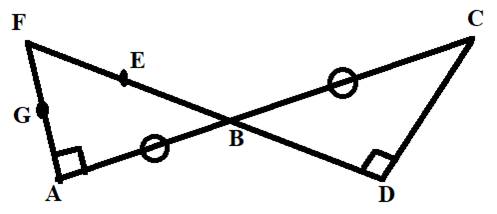
Concept Used:

Two or more lines are said to be intersecting if they cross each other at single point.

Calculation:

Since, line can move in both direction of it end points indefinitely. Here line FE when extended to point D it intersects AC at point B.

Conclusion:

Line FE when extended to point D it intersects AC at point B.

g.

To determine

To Find: The missing terms for the given blank.

Answer to Problem 3PSA

  $\overline{AG}\cap \overline{GF}=\underset{\_}{G}$

Explanation of Solution

Given:

  

  $\overline{AG}\cap \overline{GF}=\_\_\_\_\_\_$

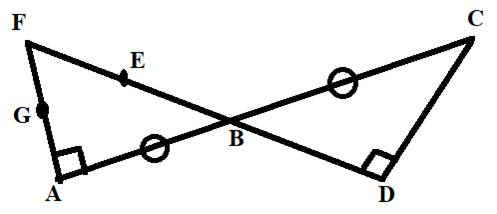
Concept Used:

Intersection of two or more line segments is the point common to both the line segments.

Calculation:

Here, point G is the point common to both the line segments AG and GF

  $\therefore \overline{AG}\cap \overline{GF}=\underset{\_}{G}$

Conclusion:

  $\overline{AG}\cap \overline{GF}=\underset{\_}{G}$

h.

To determine

To Find: The missing terms for the given blank.

Answer to Problem 3PSA

  $\overline{AG}\cup \overline{GF}=\underset{\_}{\overline{AF}}$

Explanation of Solution

Given:

  

  $\overline{AG}\cup \overline{GF}=\_\_\_\_\_\_$

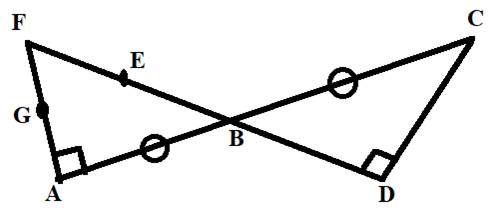
Concept Used:

Union of two or more line segments is the combination of all the line segments and get a single line whose length is the sum of all line segments taking part in union operations.

Calculation:

Here, line segments AG and GF when joined together using the point G, we get a line segment AF

  $\therefore \overline{AG}\cup \overline{GF}=\underset{\_}{\overline{AF}}$

Conclusion:

  $\overline{AG}\cup \overline{GF}=\underset{\_}{\overline{AF}}$

i.

To determine

To Find: A ray whose initial point is B and endpoint is E.

Answer to Problem 3PSA

  $\overrightarrow{BE}$

Explanation of Solution

Given:

  

Concept Used:

A ray is a line which has a initial point but no ending point.

Calculation:

Here, the ray $\overrightarrow{BE}$ have a initial point B and passing through the point E.

Conclusion:

  $\overrightarrow{BE}$

j.

To determine

To Find: All points between point F and point D.

Answer to Problem 3PSA

Point E and point B

Explanation of Solution

Given:

  

Concept Used:

Point is a geometrical term having no dimension, i.e., no length, breadth and thickness.

Calculation:

Here, points E and B lies between F and D.

Conclusion:

Points E and B