Geometry For Enjoyment And Challenge
91st Edition
ISBN: 9780866099653
Author: Richard Rhoad, George Milauskas, Robert Whipple
Publisher: McDougal Littell
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 1, Problem 1RP
a
To determine
The possible names of the line containing the points.
a
Expert Solution
Answer to Problem 1RP
Possible names are
Explanation of Solution
Given information:
A quadrilateral ABCD
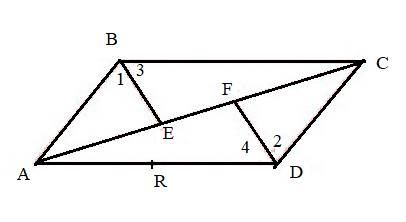
So, the possible name of line segment can be
b.
To determine
b.
Expert Solution
Answer to Problem 1RP
The side containing the angle ∠ABC is AB and BC.
Explanation of Solution
Given information:
A quadrilateral ABCD
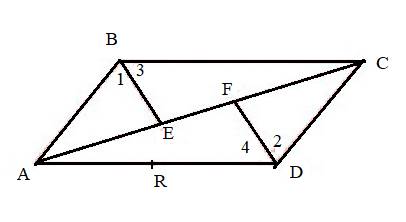
The side containing the angle ∠ABC is AB and BC.
c.
To determine
c.
Expert Solution
Answer to Problem 1RP
The common side of ∠2 and ∠4 is DF
Explanation of Solution
Given information:
A quadrilateral ABCD
The common side of ∠2 and ∠4 is DF
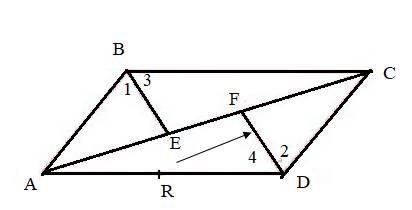
d.
To determine
d.
Expert Solution
Answer to Problem 1RP
The horizontal ray containing the end point C is BC.
Explanation of Solution
Given information:
A quadrilateral ABCD
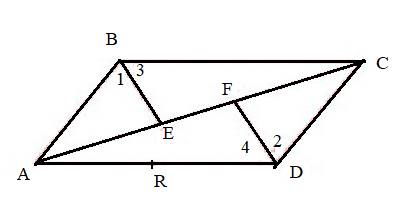
A ray is defined as a part of a line with a start point but no end point.
The horizontal ray containing the end point C is BC.
e.
To determine
e.
Expert Solution
Answer to Problem 1RP
∠BAD
∠2
∠ABC
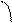
Explanation of Solution
Given information:
A quadrilateral ABCD
f.
To determine
To find whether the two angle are same.
f.
Expert Solution
Answer to Problem 1RP
Both the angles are same.
Explanation of Solution
Given information:
A quadrilateral ABCD
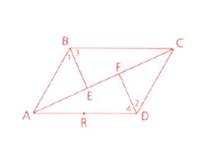
The angle FCD and angle DCE represent the same angle as point E and F are on the same line segment.
g.
To determine
g.
Expert Solution
Answer to Problem 1RP
The angle B is the angle containing the side AB and BC.
Explanation of Solution
Given information:
A quadrilateral ABCD
The side containing the angle ∠ABC is AB and BC.
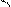
h.
To determine
h.
Expert Solution
Answer to Problem 1RP
Explanation of Solution
Given information:
A quadrilateral ABCD
Ray FC is on ray EC so their union is EC.
i.
To determine
i.
Expert Solution
Answer to Problem 1RP
Explanation of Solution
Given information:
A quadrilateral ABCD
Common part in ray EC and FA is segment EF
j.
To determine
j.
Expert Solution
Answer to Problem 1RP
Explanation of Solution
Given information:
A quadrilateral ABCD
Ray BA and ray BE together forms ∠ABE
k.
To determine
k.
Expert Solution
Answer to Problem 1RP
Explanation of Solution
Given information:
A quadrilateral ABCD
Line AC and DR intersect at point A.
l.
To determine
l.
Expert Solution
Answer to Problem 1RP
Explanation of Solution
Given information:
A quadrilateral ABCD
Angle AFD and line segment CE both intersect to give line segment EF.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Chapter 1 Solutions
Geometry For Enjoyment And Challenge
Ch. 1.1 - Prob. 1PSACh. 1.1 - Prob. 2PSACh. 1.1 - Prob. 3PSACh. 1.1 - Prob. 4PSACh. 1.1 - Prob. 5PSACh. 1.1 - Prob. 6PSACh. 1.1 - Prob. 7PSACh. 1.1 - Prob. 8PSACh. 1.1 - Prob. 9PSACh. 1.1 - Prob. 10PSA
Ch. 1.1 - Prob. 11PSBCh. 1.1 - Prob. 12PSBCh. 1.1 - Prob. 13PSCCh. 1.1 - Prob. 14PSCCh. 1.2 - Prob. 1PSACh. 1.2 - Prob. 2PSACh. 1.2 - Prob. 3PSACh. 1.2 - Prob. 4PSACh. 1.2 - Prob. 5PSACh. 1.2 - Prob. 6PSACh. 1.2 - Prob. 7PSACh. 1.2 - Prob. 8PSACh. 1.2 - Prob. 9PSACh. 1.2 - Prob. 10PSACh. 1.2 - Prob. 11PSACh. 1.2 - Prob. 12PSBCh. 1.2 - Prob. 13PSBCh. 1.2 - Prob. 14PSBCh. 1.2 - Prob. 15PSBCh. 1.2 - Prob. 16PSBCh. 1.2 - Prob. 17PSBCh. 1.2 - Prob. 18PSBCh. 1.2 - Prob. 19PSCCh. 1.2 - Prob. 20PSCCh. 1.2 - Prob. 21PSCCh. 1.2 - Prob. 22PSCCh. 1.2 - Prob. 23PSCCh. 1.3 - Prob. 1PSACh. 1.3 - Prob. 2PSACh. 1.3 - Prob. 3PSACh. 1.3 - Prob. 4PSACh. 1.3 - Prob. 5PSACh. 1.3 - Prob. 6PSACh. 1.3 - Prob. 7PSACh. 1.3 - Prob. 8PSACh. 1.3 - Prob. 9PSACh. 1.3 - Prob. 10PSBCh. 1.3 - Prob. 11PSBCh. 1.3 - Prob. 12PSBCh. 1.3 - Prob. 13PSBCh. 1.3 - Prob. 14PSBCh. 1.3 - Prob. 15PSCCh. 1.3 - Prob. 16PSCCh. 1.3 - Prob. 17PSCCh. 1.4 - Prob. 1PSACh. 1.4 - Prob. 2PSACh. 1.4 - Prob. 3PSACh. 1.4 - Prob. 4PSACh. 1.4 - Prob. 5PSACh. 1.4 - Prob. 6PSACh. 1.4 - Prob. 7PSACh. 1.4 - Prob. 8PSACh. 1.4 - Prob. 9PSACh. 1.4 - Prob. 10PSACh. 1.4 - Prob. 11PSBCh. 1.4 - Prob. 12PSBCh. 1.4 - Prob. 13PSBCh. 1.4 - Prob. 14PSCCh. 1.4 - Prob. 15PSCCh. 1.5 - Prob. 1PSACh. 1.5 - Prob. 2PSACh. 1.5 - Prob. 3PSACh. 1.5 - Prob. 4PSACh. 1.5 - Prob. 5PSACh. 1.5 - Prob. 6PSACh. 1.5 - Prob. 7PSACh. 1.5 - Prob. 8PSACh. 1.5 - Prob. 9PSACh. 1.5 - Prob. 10PSACh. 1.5 - Prob. 11PSACh. 1.5 - Prob. 12PSACh. 1.5 - Prob. 13PSACh. 1.5 - Prob. 14PSACh. 1.5 - Prob. 15PSACh. 1.5 - Prob. 16PSACh. 1.5 - Prob. 17PSACh. 1.5 - Prob. 18PSBCh. 1.5 - Prob. 19PSBCh. 1.5 - Prob. 20PSBCh. 1.5 - Prob. 21PSBCh. 1.5 - Prob. 22PSCCh. 1.5 - Prob. 23PSCCh. 1.5 - Prob. 24PSCCh. 1.6 - Prob. 1PSACh. 1.6 - Prob. 2PSACh. 1.6 - Prob. 3PSACh. 1.6 - Prob. 4PSACh. 1.6 - Prob. 5PSACh. 1.6 - Prob. 6PSACh. 1.6 - Prob. 7PSBCh. 1.6 - Prob. 8PSBCh. 1.6 - Prob. 9PSBCh. 1.6 - Prob. 10PSCCh. 1.6 - Prob. 11PSCCh. 1.6 - Prob. 12PSDCh. 1.7 - Prob. 1PSACh. 1.7 - Prob. 2PSACh. 1.7 - Prob. 3PSACh. 1.7 - Prob. 4PSACh. 1.7 - Prob. 5PSACh. 1.7 - Prob. 6PSACh. 1.7 - Prob. 7PSACh. 1.7 - Prob. 8PSBCh. 1.7 - Prob. 9PSBCh. 1.7 - Prob. 10PSBCh. 1.7 - Prob. 11PSBCh. 1.7 - Prob. 12PSBCh. 1.7 - Prob. 13PSCCh. 1.7 - Prob. 14PSCCh. 1.8 - Prob. 1PSACh. 1.8 - Prob. 2PSACh. 1.8 - Prob. 3PSACh. 1.8 - Prob. 4PSACh. 1.8 - Prob. 5PSACh. 1.8 - Prob. 6PSBCh. 1.8 - Prob. 7PSBCh. 1.8 - Prob. 8PSBCh. 1.8 - Prob. 9PSBCh. 1.8 - Prob. 10PSCCh. 1.9 - Prob. 1PSACh. 1.9 - Prob. 2PSACh. 1.9 - Prob. 3PSACh. 1.9 - Prob. 4PSACh. 1.9 - Prob. 5PSACh. 1.9 - Prob. 6PSBCh. 1.9 - Prob. 7PSBCh. 1.9 - Prob. 8PSBCh. 1.9 - Prob. 9PSBCh. 1.9 - Prob. 10PSBCh. 1.9 - Prob. 11PSBCh. 1.9 - Prob. 12PSCCh. 1.9 - Prob. 13PSCCh. 1.9 - Prob. 14PSCCh. 1.9 - Prob. 15PSCCh. 1 - Prob. 1RPCh. 1 - Prob. 2RPCh. 1 - Prob. 3RPCh. 1 - Prob. 4RPCh. 1 - Prob. 5RPCh. 1 - Prob. 6RPCh. 1 - Prob. 7RPCh. 1 - Prob. 8RPCh. 1 - Prob. 9RPCh. 1 - Prob. 10RPCh. 1 - Prob. 11RPCh. 1 - Prob. 12RPCh. 1 - Prob. 13RPCh. 1 - Prob. 14RPCh. 1 - Prob. 15RPCh. 1 - Prob. 16RPCh. 1 - Prob. 17RPCh. 1 - Prob. 18RPCh. 1 - Prob. 19RPCh. 1 - Prob. 20RPCh. 1 - Prob. 21RPCh. 1 - Prob. 22RPCh. 1 - Prob. 23RPCh. 1 - Prob. 24RPCh. 1 - Prob. 25RPCh. 1 - Prob. 26RPCh. 1 - Prob. 27RPCh. 1 - Prob. 28RPCh. 1 - Prob. 29RPCh. 1 - Prob. 30RPCh. 1 - Prob. 31RPCh. 1 - Prob. 32RPCh. 1 - Prob. 33RPCh. 1 - Prob. 34RPCh. 1 - Prob. 35RPCh. 1 - Prob. 36RPCh. 1 - Prob. 37RPCh. 1 - Prob. 38RPCh. 1 - Prob. 39RPCh. 1 - Prob. 40RPCh. 1 - Prob. 41RPCh. 1 - Prob. 42RPCh. 1 - Prob. 43RP
Additional Math Textbook Solutions
Find more solutions based on key concepts
4. Correlation and Causation What is meant by the statement that “correlation does imply causation”?
Elementary Statistics
Fill in each blank so that the resulting statement is true. The quadratic function f(x)=a(xh)2+k,a0, is in ____...
Algebra and Trigonometry (6th Edition)
Disks/washers about the y-axis Let R be the region bounded by the following curves. Use the disk or washer meth...
Calculus: Early Transcendentals (2nd Edition)
To find the player’s average batting fraction in the lowest term when the batting average is .225 .
Pre-Algebra Student Edition
Stating the Null and Alternative Hypotheses In Exercises 25–30, write the claim as a mathematical statement. St...
Elementary Statistics: Picturing the World (7th Edition)
1. How many solutions are there to ax + b = 0 with ?
College Algebra with Modeling & Visualization (5th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- In the graph below triangle I'J'K' is the image of triangle UK after a dilation. 104Y 9 CO 8 7 6 5 I 4 3 2 J -10 -9 -8 -7 -6 -5 -4 -3 -21 1 2 3 4 5 6 7 8 9 10 2 K -3 -4 K' 5 -6 What is the center of dilation? (0.0) (-5. 2) (-8. 11 (9.-3) 6- 10arrow_forwardSelect all that apply. 104 8 6 4 2 U U' -10 -8 -6 4 -2 2 4 6 10 -2 V' W' -4 -6 -8 -10 W V Select 2 correct answerts! The side lengths are equal in measure. The scale factor is 1/5. The figure has been enlarged in size. The center of dilation is (0.0) 8 10 Xarrow_forwardIn the graph below triangle I'J'K' is the image of triangle UK after a dilation. 104Y 9 CO 8 7 6 5 I 4 3 2 J -10 -9 -8 -7 -6 -5 -4 -3 -21 1 2 3 4 5 6 7 8 9 10 2 K -3 -4 K' 5 -6 What is the center of dilation? (0.0) (-5. 2) (-8. 11 (9.-3) 6- 10arrow_forward
- Qll consider the problem -abu+bou+cu=f., u=0 ondor I prove atu, ul conts. @ if Blu,v) = (b. 14, U) + ((4,0) prove that B244) = ((c- — ob)4;4) ③if c±vbo prove that acuius v. elliptic.arrow_forwardQ3: Define the linear functional J: H₁(2) R by ¡(v) = a(v, v) - L(v) Л Let u be the unique weak solution to a(u,v) = L(v) in H(2) and suppose that a(...) is a symmetric bilinear form on H(2) prove that 1- u is minimizer. 2- u is unique. 3- The minimizer J(u) can be rewritten under 1(u) = u Au-ub, algebraic form 1 2 Where A, b are repictively the stiffence matrix and the load vector Q4: A) Answer 1- show that the solution to -Au = f in A, u = 0 on a satisfies the stability Vullfll and show that ||V(u u)||||||2 - ||vu||2 2- Prove that Where lu-ul Chuz - !ull = a(u, u) = Vu. Vu dx + fu. uds B) Consider the bilinea forta Л a(u, v) = (Au, Av) (Vu, Vv + (Vu, v) + (u,v) Show that a(u, v) continues and V- elliptic on H(2)arrow_forward7) In the diagram below of quadrilateral ABCD, E and F are points on AB and CD respectively, BE=DF, and AE = CF. Which conclusion can be proven? A 1) ED = FB 2) AB CD 3) ZA = ZC 4) ZAED/CFB E B D 0arrow_forward
- 1) In parallelogram EFGH, diagonals EG and FH intersect at point I such that EI = 2x - 2 and EG = 3x + 11. Which of the following is the length of GH? a) 15 b) 28 c) 32 d) 56arrow_forward5) Which of the following are properties of all squares: 1. Congruent diagonals 2. Perpendicular diagonals 3. Diagonals that bisect vertex angles a) 1 and 2 only b) 1 and 3 only c) 2 and 3 only d) 1, 2, and 3arrow_forward6) In an isosceles trapezoid HIJK it is known that IJ || KH. Which of the following must also be true? a) IJ = KH b) HIJK c) HIJK d) IJ KHarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
01 - Angles and Angle Measure in Degrees - Part 1 - Types of Angles & What is an Angle?; Author: Math and Science;https://www.youtube.com/watch?v=hy95VyPet-M;License: Standard YouTube License, CC-BY