Chapter 1.2, Problem 12PSB

a.

To determine

To find: The number of triangles in the given figure.

Answer to Problem 12PSB

There are eight triangles in the given figure.

Explanation of Solution

Given:

  

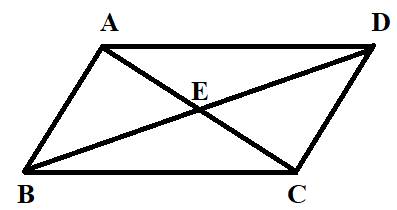
A parallelogram ABCD having diagonals AC and BD intersecting at E.

Concept Used:

Triangle is a three sided closed polygon.

Calculation:

Here, we have a parallelogram ABCD having diagonals AC and BD intersecting at E shown as

  

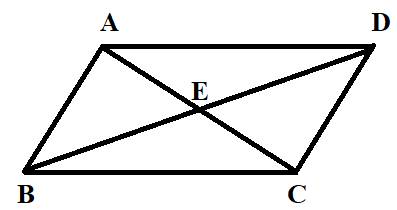
As we know that Triangle is a three sided closed polygon.

The triangles in the given figure are

  $\begin{array}{l}△AED,△EDC,△ECB,△EBA,\\ △ADC,△DCB,△CBA,△ABD\end{array}$

Thus, there are eight triangles in the given figure.

Conclusion:

There are eight triangles in the given figure.

b.

To determine

To find: The number of angles in the given figure.

Answer to Problem 12PSB

There are 12 angles in the given figure.

Explanation of Solution

Given:

  

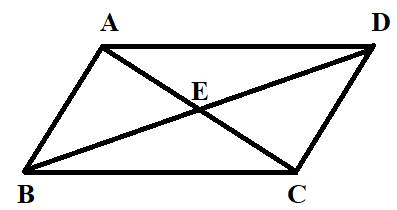
A parallelogram ABCD having diagonals AC and BD intersecting at E.

Concept Used:

Two lines passing through a single point known as vertex forms an angle.

Calculation:

Here, we have a parallelogram ABCD having diagonals AC and BD intersecting at E shown as

  

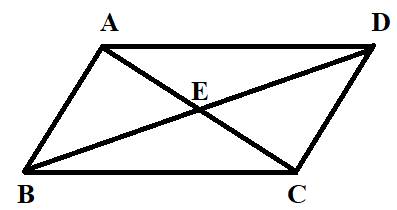
As we know that angle is formed when two lines passing through a single point known as vertex.

Angles in the given figure are

  $\begin{array}{l}\angle EAD,\angle AED,\angle ADE,\angle EDC,\angle DEC,\angle ECD,\\ \angle ECB,\angle BEC,\angle CBE,\angle EAB,\angle AEB,\angle ABE\end{array}$

Thus, there are 12 angles in the given figure.

Conclusion:

There are 12 angles in the given figure.

c.

To determine

To find: The number of angles appears to be acute angle in the given figure.

Answer to Problem 12PSB

There are 6 acute angles in the given figure.

Explanation of Solution

Given:

  

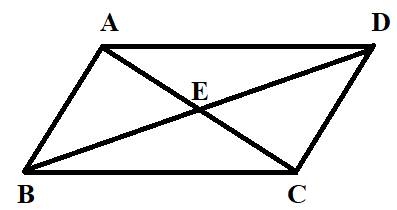
A parallelogram ABCD having diagonals AC and BD intersecting at E.

Concept Used:

Two lines passing through a single point known as vertex forms an angle. Acute angle is the angle whose measure is greater than zero degree but less than 90 degrees.

Calculation:

Here, we have a parallelogram ABCD having diagonals AC and BD intersecting at E shown as

  

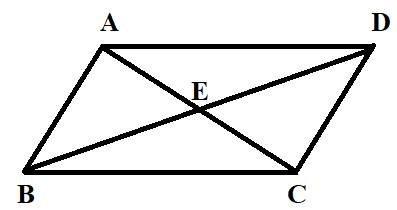
As we know that angle is formed when two lines passing through a single point known as vertex.

Acute angles in the given figure are

  $\begin{array}{l}\angle EAD,\angle ADE,\angle EDC,\angle ECD,\\ \angle ECB,\angle CBE,\angle EAB,\angle ABE\end{array}$

Thus, there are 6 acute angles in the given figure.

Conclusion:

There are 6 acute angles in the given figure.

d.

To determine

To find: The number of angles appears to be obtuse angle in the given figure.

Answer to Problem 12PSB

There are 4 obtuse angles in the given figure.

Explanation of Solution

Given:

  

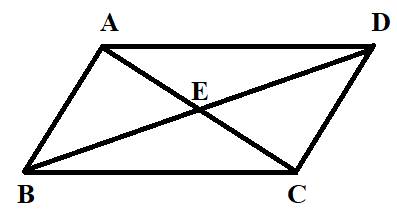
A parallelogram ABCD having diagonals AC and BD intersecting at E.

Concept Used:

Two lines passing through a single point known as vertex forms an angle. Obtuse angle is the angle whose measure is greater than 90 degrees but less than 180 degrees.

Calculation:

Here, we have a parallelogram ABCD having diagonals AC and BD intersecting at E shown as

  

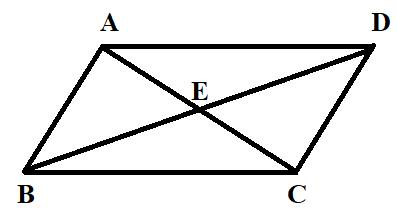
As we know that angle is formed when two lines passing through a single point known as vertex.

Obtuse angles in the given figure are

  $\angle AED,\angle DEC,\angle BEC,\angle AEB$

Thus, there are 4 obtuse angles in the given figure.

Conclusion:

There are 4 obtuse angles in the given figure.

e.

To determine

To find: The straight angles angle in the given figure.

Answer to Problem 12PSB

  $\angle AEC\text{ and}\angle DEB$ are the straight angles in the given figure.

Explanation of Solution

Given:

  

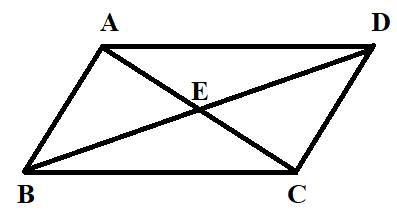
A parallelogram ABCD having diagonals AC and BD intersecting at E.

Concept Used:

Two lines passing through a single point known as vertex forms an angle. Straight angle is the angle whose measure is equal to 180 degrees.

Calculation:

Here, we have a parallelogram ABCD having diagonals AC and BD intersecting at E shown as

  

As we know that angle is formed when two lines passing through a single point known as vertex.

Straight angles in the given figure formed using the given diagonal, thus the straight angles are

  $\angle AEC\text{ and}\angle DEB$

Thus, there are two straight angles in the given figure.

Conclusion:

  $\angle AEC\text{ and}\angle DEB$ are the straight angles in the given figure.