Chapter 12.7, Problem 43E

Law of Cosines The side lengths of any triangle are related by the Law of Cosines.

c² = a² + b² – 2ab cos θ.

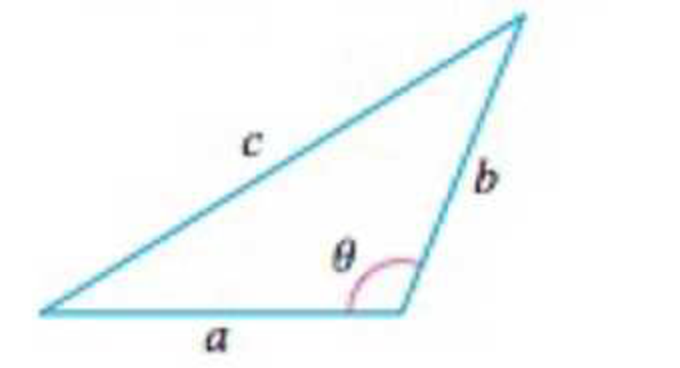
a.    Estimate the change in the side length c when a changes from a = 2 to a = 2.03, b changes from b = 4.00 to b = 3.96, and θ changes from $\theta =\pi /3$ to $\theta =\pi /3+\pi /90$.

b.    If a changes from a = 2 to a = 2.03 and b changes from b = 4.00 to b = 3.96, is the resulting change in c greater in magnitude when $\theta =\pi /20$ (small angle) or when $\theta =9\pi /20$ (close to a right angle)?