
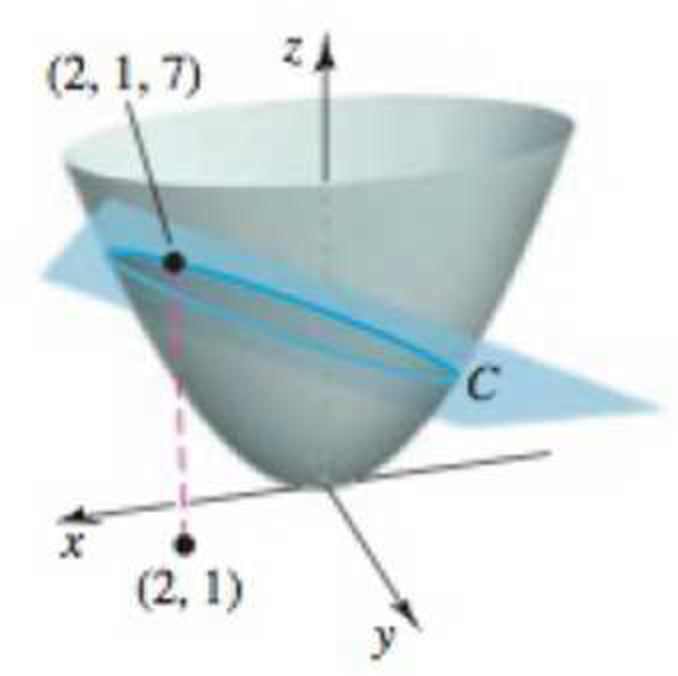
Line tangent to an intersection curve Consider the paraboloid z = x2 + 3y2 and the plane z = x + y + 4, which intersects the paraboloid in a curve C at (2, 1, 7) (see figure). Find the equation of the line tangent to C at the point (2.1, 7). Proceed as follows.
a. Find a vector normal to the plane at (2, 1, 7).
b. Find a vector normal to the plane tangent to the paraboloid at (2,1,7).
c. Argue that the line tangent to C at (2, 1, 7) is orthogonal to both normal
d. Knowing a point on the tangent line and the direction of the tangent line, write an equation of the tangent line in parametric form.
Want to see the full answer?
Check out a sample textbook solution
Chapter 12 Solutions
CODE/CALC ET 3-HOLE
Additional Engineering Textbook Solutions
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Algebra and Trigonometry (6th Edition)
Pre-Algebra Student Edition
Elementary Statistics: Picturing the World (7th Edition)
Elementary Statistics (13th Edition)
- 4x-3 2. Determine the interval over which the function is continuous. x+4arrow_forward1. Find the average rate of change for the following functions over the given intervals. a) f(x)=4x-2x²+3x between x=-1 and x=4 b) y lnx between x=1 and x=4arrow_forward1. Find all values x=a where the function is discontinuous, determine if the discontinuity is removable or non- removable. For each value of x, give the limit of the function as x approaches a. Be sure to note when the limit doesn't exist and explain how you know. a) f(x)= 2-x x²(x+5) b) f(x)= x²-9x x²+3x c) p(x)=-3x²+2x²+5x-8arrow_forward
- Do the Laplace Transformation and give the answer in Partial Fractions. Also do the Inverted Laplace Transformation and explain step-by-step.arrow_forward12. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.508.XP. ASK YOUR TEA Make a substitution to express the integrand as a rational function and then evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) x + 16 dx X Need Help? Read It SUBMIT ANSWER 13. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.512.XP. ASK YOUR TEA Make a substitution to express the integrand as a rational function and then evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) dx 8)(2x + 1) Need Help? Read It SUBMIT ANSWER 14. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.518.XP. Find the area of the region under the given curve from 1 to 5. y = x² +7 6x - x² Need Help? Read It ASK YOUR TEAarrow_forwardDETAILS MY NOTES SESSCALCET2 6.3.012. 6. [-/1 Points] Evaluate the integral. x-4 dx x² - 5x + 6 Need Help? Read It SUBMIT ANSWER 7. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.019. Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) x²+1 (x-6)(x-5)² dx Need Help? Read It SUBMIT ANSWER 8. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.021. Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) ✓ x² 4 +4 dxarrow_forward
- DETAILS MY NOTES SESSCALCET2 6.3.017. 1. [-/1 Points] Evaluate the integral. - - dy y(y + 2)(y-3) Need Help? Read It Watch It SUBMIT ANSWER 2. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.027. Evaluate the integral. (Use C for the constant of integration.) X + 16 x²+10x29 dx Need Help? Read It Watch It SUBMIT ANSWERarrow_forwardDo the Laplace Transformation for this equation in Partial Fractions.arrow_forwardUse undetermined coefficients to find the particular solution to y"-2y-4y=3t+6 Yp(t) =arrow_forward
- Car A starts from rest at t = 0 and travels along a straight road with a constant acceleration of 6 ft/s^2 until it reaches a speed of 60ft/s. Afterwards it maintains the speed. Also, when t = 0, car B located 6000 ft down the road is traveling towards A at a constant speed of 80 ft/s. Determine the distance traveled by Car A when they pass each other.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forward
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning




