Chapter 12, Problem 83RE

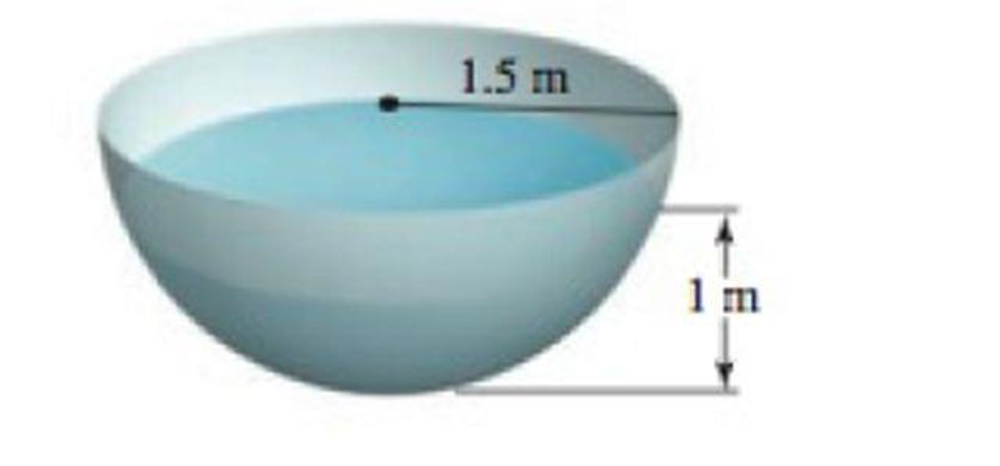
Water-level changes A hemispherical tank with a radius of 1.50 m is filled with water to a depth of 1.00 m. Water is released from the tank and the water level drops by 0.05 m (from 1.00 m to 0.95 m).

a.    Approximate the change in the volume of water in the tank. The volume of a spherical cap is V = πh²(3r – h)/3, where r is the radius of the sphere and h is the thickness of the cap (in this case, the depth of the water).

b.    Approximate the change in the surface area of the water in the tank.