The exergy destruction associated with each process of the Brayton cycle and the exergy of the exhaust gases at the exit of the regenerator.

Question

Want to see more full solutions like this?

Answer 1

Question

Chapter 9.12, Problem 150P

To determine

The exergy destruction associated with each process of the Brayton cycle and the exergy of the exhaust gases at the exit of the regenerator.

Expert Solution & Answer

Answer to Problem 150P

The exergy destruction associated with process 1-2 for Brayton cycle is 38.42 kJ/kg.

The exergy destruction associated with process 3-4 for Brayton cycle is 24.23 kJ/kg.

The exergy destruction associated with regeneration process for Brayton cycle is 4.47 kJ/kg.

The exergy destruction associated with process 5-3 for Brayton cycle is 24.16 kJ/kg.

The exergy destruction associated with process 6-1 for Brayton cycle is 148.7 kJ/kg.

The exergy of the exhaust gases at the exit of the regenerator is 148.9 kJ/kg.

Explanation of Solution

Draw T−s diagram for regenerative Brayton cycle as shown in Figure (1).

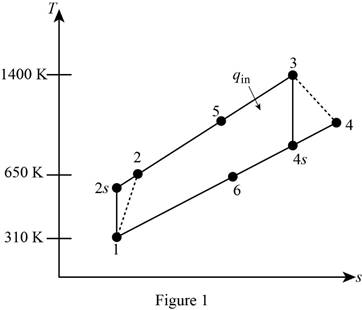
THERMODYNAMICS (LL)-W/ACCESS >CUSTOM<, Chapter 9.12, Problem 150P

Write the expression of pressure ratio for the regenerative Brayton cycle (rp).

rp=P2/P1 (I)

Here, pressure at state 2 is P2 and pressure at state 1 is P1

Write the pressure ratio and pressure relation for the process 3-4.

Pr4=P4P3Pr3 (II)

Here, pressure at state 3 is P3, pressure at state 4 is P4 , relative pressure at state 4 is Pr4 and relative pressure at state 3 is Pr3.

Write the expression of efficiency of the turbine (ηT).

ηT=h3−h4h3−h4sh4=h3−ηT(h3−h4s) (III)

Here, enthalpy at state 3 is h3 , enthalpy at state 4 is h4 and enthalpy on isentropic state 4s is h4s.

Write the expression of heat added due to regeneration (qregen).

qregen=ε(h4−h2) (IV)

Here, the effectiveness of the regenerator is ε and enthalpy at state 2 is h2.

Write the expression of net work output of the regenerative Brayton cycle (wnet).

wnet=wT,out−wC,in

wnet=(h3−h4)−(h2−h1) (V)

Here, the work output by the turbine is wT,out, and the work input to the compressor is wC,in.

Write the expression of heat input to the regenerative Brayton cycle (qin).

qin=(h3−h2)−qregen (VI)

Write the expression of heat rejected by the regenerative Brayton cycle (qout).

qout=qin−wnet (VII)

Write the expression of specific enthalpy at state 6 (h6), using the heat rejection relation.

h6=h1+qout (VIII)

Write the specific enthalpy relation for the regenerator.

h5−h2=h4−h6h5=(h4−h6)+h2 (IX)

Write the expression of exergy destruction associated with the process 1-2 for Brayton cycle (xdestroyed,12).

xdestroyed,12=T0(s2−s1)

xdestroyed,12=T0(s2∘−s1∘−RlnP2P1) (X)

Here, the gas constant of air is R, entropy of air at state 2 as a function of temperature only is s2∘, , entropy of air at state 1 as a function of temperature only is s1∘ and the temperature of the surroundings is T0.

Write the expression of exergy destruction for process 3-4 (xdestroyed,34).

xdestroyed,34=T0(s4−s3)

xdestroyed,34=T0(s4∘−s3∘−RlnP4P3) (XI)

Here, entropy of air at state 3 as a function of temperature is s3∘, and entropy of air at state 4 as a function of temperature is s4∘.

Write the expression of exergy destruction for Brayton cycle (xdestroyed,regen).

xdestroyed,regen=T0[(s5−s2)+(s6−s4)]

xdestroyed,regen=T0[(s5∘−s2∘)+(s6∘−s4∘)] (XII)

Here, entropy of air at state 5 as a function of temperature alone is s5∘, and entropy of air at state 6 as a function of temperature alone is s6∘.

Write the expression of exergy destruction for process 5-3 (xdestroyed,53).

xdestroyed,53=T0(s3−s5+−qinTH)

xdestroyed,53=T0(s3∘−s5∘−RlnP3P5−qinTH) (XIII)

Here, the temperature of the heat source is TH.

Write the expression of exergy destruction for process 6-1 (xdestroyed,61).

xdestroyed,61=T0(s1−s6+qoutTL)

xdestroyed,61=T0(s1∘−s6∘−RlnP1P6+qoutTL) (XIV)

Here, the temperature of the sink is TL.

Write the expression of stream exergy at the exit of the regenerator (state 6) (ϕ6).

ϕ6=(h6−h0)−T0(s6−s0) (XV)

Here, the specific enthalpy of the surroundings is h0.

Write the expression of change entropy for the exit of the regenerator (s6−s0).

s6−s0=s6∘−s0∘−RlnP6P1 (XVI)

Here, entropy of air at the surroundings as a function of temperature alone is s0∘, and the pressure of air at the surroundings is P0.

Conclusion:

Refer Table A-17, “Ideal gas properties of air”, obtain the properties of air at 310 K (T1), 650K (T2) and 1400 K (T3), as 310.24 kJ/kg for h1, 659.84 kJ/kg for h2, 1,515.42 kJ/kg for h3 and 450.5 for Pr3 respectively.

Substitute 900 kPa for P2, and 100 kPa for P1 in Equation (I).

rp=900 kPa/100 kPa=9

Substitute 19 for P4P3, and 450.5 for Pr3 in Equation (II).

Pr4=(19)(450.5)=50.06

Refer Table A-17, “Ideal gas properties of air”, obtain the properties of air at 50.06 (Pr4), as 832.44 kJ/kg for h4s.

Substitute 1,515.42 kJ/kg for h3, 832.44 kJ/kg for h4s, and 0.90 for ηT.

h4=h3−ηT(h3−h4s)=1,515.42 kJ/kg+(0.90)(1,515.42−832.44) kJ/kg=900.74 kJ/kg

Substitute 0.80 for ε, 900.74 kJ/kg for h4, and 659.84 kJ/kg for h2 in Equation (IV).

qregen=(0.80)(900.74−659.84) kJ/kg=192.7 kJ/kg

Substitute 1,515.42 kJ/kg for h3, 900.74 kJ/kg for h4, 659.84 kJ/kg for h2, and 310.24 kJ/kg for h1 in Equation (V).

wnet=(1,515.42−900.74) kJ/kg−(659.84−310.24) kJ/kg=265.08 kJ/kg

Substitute 192.7 kJ/kg for qregen, 1,515.42 kJ/kg for h3, and 659.84kJ/kg for h2 in Equation (VI).

qin=[(1,515.42−659.84)−192.7] kJ/kg=662.88 kJ/kg

Substitute 662.88 kJ/kg for qin, and 265.08 kJ/kg for wnet in Equation (VII).

qout=(662.88−265.08) kJ/kg=397.80 kJ/kg

Substitute 310.24 kJ/kg for h1, and 397.80 kJ/kg for qout in Equation (VIII).

h6=(310.24+397.80) kJ/kg=708.04 kJ/kg

Substitute 659.84 kJ/kg for h2, 900.74 kJ/kg for h4, and 708.04 kJ/kg for h6.

h5=(h4−h6)+h2=(900.74−708.04) kJ/kg+659.84 kJ/kg=852.54 kJ/kg

Refer Table A-17, “Ideal gas properties of air”, obtain the properties of air at 310 K (T1), 659.84 kJ/kg (h2), 1400 K (T3), 900.74 kJ/kg (h4), 852.54 kJ/kg (h5) and 708.04 kJ/kg (h6) as 1.73498 kJ/kg⋅K for s10, 2.49364 kJ/kg⋅K for s20, 3.36200 kJ/kg⋅K for s30, 2.81216 kJ/kg⋅K for s40,2.75537 kJ/kg⋅K for s50, and 2.56525 kJ/kg⋅K for s60.

Substitute 300 K for T0, 1.73498 kJ/kg⋅K for s1∘, 2.49364 kJ/kg⋅K for s2∘, 0.287 kJ/kg⋅K for R, and 9 for P2P1 in Equation (X).

xdestroyed,12=(300 K)[(2.49364−1.73498)kJ/kg⋅K−(0.287kJ/kg⋅K)ln(9)]=38.42 kJ/kg

Thus, the exergy destruction associated with process 1-2 for Brayton cycle is 38.42 kJ/kg.

Substitute 300 K for T0, 3.36200 kJ/kg⋅K for s3∘, 2.81216 kJ/kg⋅K for s4∘, 0.287 kJ/kg⋅K for R, and 19 for P4P3 in Equation (XI).

xdestroyed,34=(300 K)[(2.81216−3.36200)kJ/kg⋅K−(0.287kJ/kg⋅K)ln(19)]=24.23 kJ/kg

Thus, the exergy destruction associated with process 3-4 for Brayton cycle is 24.23 kJ/kg.

Substitute 300 K for T0, 2.75537 kJ/kg⋅K for s5∘, 2.81216 kJ/kg⋅K for s4∘, 2.49364 kJ/kg⋅K for s2∘, and 2.56525 kJ/kg⋅K for s6∘ in Equation (XII).

xdestroyed,regen=(300 K)[(2.75537−2.49364)kJ/kg⋅K+(2.56525−2.81216) kJ/kg⋅K]=4.47 kJ/kg

Thus, the exergy destruction associated with regeneration process for Brayton cycle is 4.47 kJ/kg.

Substitute 300 K for T0, 3.36200 kJ/kg⋅K for s3∘, 2.75537 kJ/kg⋅K for s5∘, 0.287 kJ/kg⋅K for R, 1260 K for TH, and 662.88 kJ/kg for qin in Equation (XIII). For the process 5-3, pressure remains constant, hence substitute 0 for lnP3P5.

xdestroyed,53=(300 K)[(3.36200−2.75537)kJ/kg⋅K−(0.287kJ/kg⋅K)(0)−662.88 kJ/kg1260 K]=24.16 kJ/kg

Thus, the exergy destruction associated with process 5-3 for Brayton cycle is 24.16 kJ/kg.

Substitute 300 K for T0, 1.73498kJ/kg⋅K for s1∘, 2.56525 kJ/kg⋅K for s6∘, 0.287 kJ/kg⋅K for R, 300 K for TL, and 397.80 kJ/kg for qout in Equation (XIV). For the process 6-1, pressure remains constant, hence substitute 0 for lnP1P6.

xdestroyed,61=(300 K)[(1.73498−2.56525)kJ/kg⋅K−(0.287kJ/kg⋅K)(0)+397.80 kJ/kg300 K]= 148.7 kJ/kg

Thus, the exergy destruction associated with process 6-1 for Brayton cycle is 148.7 kJ/kg.

Refer Table A-17, “Ideal gas properties of air”, obtain the properties of air at 300 K (T0) as 1.70203 kJ/kg⋅K for s00 and 300.19 kJ/kg for h0.

Substitute 2.56525 kJ/kg⋅K for s6∘, and 1.70203 kJ/kg⋅K for s0∘ in Equation (XVI). Also, at the exit of the regenerator, pressure remains constant, hence substitute 0 for lnP6P1.

s6−s0=(2.56525−1.70203) kJ/kg⋅K=0.86322 kJ/kg⋅K

Substitute 708.04 kJ/kg for h6, 300.19 kJ/kg for h0, 300 K for T0, and 0.86322 kJ/kg⋅K for (s6−s0) in Equation (XV).

ϕ6=(h6−h0)−T0(s6−s0)=(708.04−300.19) kJ/kg−(300 K)(0.86322 kJ/kg⋅K )=148.9 kJ/kg

Thus, the exergy of the exhaust gases at the exit of the regenerator is 148.9 kJ/kg.

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Students have asked these similar questions

### Make an introduction to a report of a rocket study project, in the OpenRocket software, where the project consists of the simulation of single-stage and two-stage rockets, estimating the values of the exhaust velocities of the engines used, as well as obtaining the graphs of "altitude", "mass ratio x t", "thrust x t" and "ψ × t".

A 6305 ball bearing is subjected to a steady 5000-N radial load and a 2000-N thrust load and uses a very clean lubricant throughout its life. If the inner race angular velocity is 500 rpm find The equivalent radial load the L10 life and the L50 life

Where on the below beam is the Maxiumum Slope likely to occur? C A; Атят B

Answer 2