
Problems 79 and 80 require the following discussion: When granular materials are allowed to fall freely, they form conical (cone-shaped) piles. The naturally occurring angle of slope, measured from the horizontal, at which the loose material comes to rest is called the angle of repose and varies for different materials. The angle of repose is related to the height and base radius of the conical pile by the equation . See the illustration.
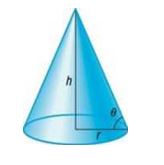
Angle of Repose: Bunker Sand The steepness of sand bunkers on a golf course is affected by the angle of repose of the sand (a larger angle of repose allows for steeper bunkers). A freestanding pile of loose sand from a United States Golf Association (USGA) bunker had a height of 4 feet and a base diameter of approximately feet.
(a) Find the angle of repose for USGA bunker sand.
(b) What is the height of such a pile if the diameter of the base is 8 feet?
(c) A 6-foot-high pile of loose Tour Grade 50/50 sand has a base diameter of approximately feet. Which type of sand (USGA or Tour Grade 50/50) would be better suited for steep bunkers?
To find:
A. The angle of repose for USGA bunker sand.
Answer to Problem 80AYU
Solution:
A. The angle of repose for the USGA bunker sand .
Explanation of Solution
Given:
Height of the freestanding pile of loose sand from USGA bunker .
Base diameter of the freestanding pile of loose sand from USGA bunker .
Radius of the freestanding pile of loose sand from USGA bunker .
Formula used:
The angle of repose .
Calculation:
To find , we need to find cos , because has the same range as except where undefined.
The angle of repose .
Here, .
Both and are positive, therefore lies in the I quadrant.
Equation of the circle .
Where .
Using the formula,
The angle of repose θ for the USGA bunker sand .
To find:
b. The height of conical USGA bunker sand pile.
Answer to Problem 80AYU
Solution:
b. The height of conical USGA bunker sand pile .
Explanation of Solution
Given:
The base diameter of conical pile .
Radius of the conical pile .
From 80 (a),
Angle of repose .
Formula used:
Calculation:
Using the formula,
Height of conical sand pile .
To find:
c. If USGA sand pile or tour grade sand is better choice for steep bunkers.
Answer to Problem 80AYU
Solution:
Angle of repose for tour grade sand is higher than USGA sand pile.
Tour grade sand is better choice for steep bunkers than USGA sand pile.
Explanation of Solution
Given:
The height of the conical Tour grade sand pile .
Base diameter of conical Tour grade sand pile .
Base radius of conical Tour grade sand pile .
Formula used:
The angle of repose .
Calculation:
To find , we need to find cos , because has the same range as except where undefined.
The angle of repose .
Here, .
Both and are positive, therefore lies in the I quadrant.
Equation of the circle .
Where .
Using the formula,
The angle of repose for the tour grade sand .
The angle of repose for the USGA bunker sand .
Angle of repose for tour grade sand is higher than USGA sand pile.
Tour grade sand is better choice for steep bunkers than USGA sand pile.
Chapter 7 Solutions
Precalculus
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
Basic Business Statistics, Student Value Edition
A First Course in Probability (10th Edition)
Elementary Statistics: Picturing the World (7th Edition)
University Calculus: Early Transcendentals (4th Edition)
Algebra and Trigonometry (6th Edition)
- Consider the function f(x) = x²-1. (a) Find the instantaneous rate of change of f(x) at x=1 using the definition of the derivative. Show all your steps clearly. (b) Sketch the graph of f(x) around x = 1. Draw the secant line passing through the points on the graph where x 1 and x-> 1+h (for a small positive value of h, illustrate conceptually). Then, draw the tangent line to the graph at x=1. Explain how the slope of the tangent line relates to the value you found in part (a). (c) In a few sentences, explain what the instantaneous rate of change of f(x) at x = 1 represents in the context of the graph of f(x). How does the rate of change of this function vary at different points?arrow_forward1. The graph of ƒ is given. Use the graph to evaluate each of the following values. If a value does not exist, state that fact. и (a) f'(-5) (b) f'(-3) (c) f'(0) (d) f'(5) 2. Find an equation of the tangent line to the graph of y = g(x) at x = 5 if g(5) = −3 and g'(5) = 4. - 3. If an equation of the tangent line to the graph of y = f(x) at the point where x 2 is y = 4x — 5, find ƒ(2) and f'(2).arrow_forwardDoes the series converge or divergearrow_forward
- Suppose that a particle moves along a straight line with velocity v (t) = 62t, where 0 < t <3 (v(t) in meters per second, t in seconds). Find the displacement d (t) at time t and the displacement up to t = 3. d(t) ds = ["v (s) da = { The displacement up to t = 3 is d(3)- meters.arrow_forwardLet f (x) = x², a 3, and b = = 4. Answer exactly. a. Find the average value fave of f between a and b. fave b. Find a point c where f (c) = fave. Enter only one of the possible values for c. c=arrow_forwardplease do Q3arrow_forward
- Use the properties of logarithms, given that In(2) = 0.6931 and In(3) = 1.0986, to approximate the logarithm. Use a calculator to confirm your approximations. (Round your answers to four decimal places.) (a) In(0.75) (b) In(24) (c) In(18) 1 (d) In ≈ 2 72arrow_forwardFind the indefinite integral. (Remember the constant of integration.) √tan(8x) tan(8x) sec²(8x) dxarrow_forwardFind the indefinite integral by making a change of variables. (Remember the constant of integration.) √(x+4) 4)√6-x dxarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





