Chapter 7.2, Problem 79AYU

Problems 79 and 80 require the following discussion: When granular materials are allowed to fall freely, they form conical (cone-shaped) piles. The naturally occurring angle of slope, measured from the horizontal, at which the loose material comes to rest is called the angle of repose and varies for different materials. The angle of repose $\theta$ is related to the height $h$ and base radius $r$ of the conical pile by the equation $\theta ={\cot }^{-1}\frac{r}{h}$. See the illustration.

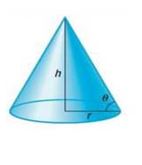
Angle of Repose: Deicing Salt Due to potential transportation issues (for example, frozen waterways) deicing salt used by highway departments in the Midwest must be ordered early and stored for future use.

When deicing salt is stored in a pile 14 feet high, the diameter of the base of the pile is 45 feet.

(a) Find the angle of repose for deicing salt.

(b) What is the base diameter of a pile that is 17 feet high?

(c) What is the height of a pile that has a base diameter of approximately 122 feet?

Source: The Salt Storage Handbook, 2013

To determine

To find:

A. The angle of repose $\theta$ for deicing salt.

Answer to Problem 79AYU

Solution:

A. The angle of repose $\theta$ for the deicing salt $={\text{ cot}}^{-1}\left(r/h\right)\approx 31.89°$.

Explanation of Solution

Given:

Height of the piled deicing salt $=h=14\text{ feet}$.

Diameter of the base of the piled deicing salt $\left(D\right)=45\text{ feet}$.

Radius of the base of the piled deicing salt $\left(r\right)=45/2\text{ feet}$.

Formula used:

The angle of repose $\theta ={\text{ cot}}^{-1}\left(r/h\right),0<\theta <\pi$.

Calculation:

To find $\theta$, we need to find $\text{cos}\theta$, because $y={\text{ cos}}^{-1}x$ has the same range as $y={\text{ cot}}^{-1}x$ except where undefined.

The angle of repose $\theta ={\text{ cot}}^{-1}\left(\left(45/2\right)/14\right),0<\theta <\pi$.

$\theta ={\text{ cot}}^{-1}\left(45/28\right),0<\theta <\pi$

$\theta ={\text{ cot}}^{-1}\left(45/28\right) ={\text{ cot}}^{-1}\left(x/y\right)$

Here, $x=45,y=28$.

Equation of the circle $=x^2+y^2 =R^2$.

Where $R=\text{ radius of the circle}$.

$R=\surd \left(x^2+y^2\right)=\surd \left({45}^2+{28}^2\right)=\surd \left({2025}^2+784\right)=\surd 2809=53$

Both $x$ and $y$ are positive, therefore $\theta$ lies in the I quadrant.

Using the formula,

$\text{cos}\theta =x/R$

$\text{cos}\theta =45/53,0<\theta <\pi /2\left(\text{I quadrant}\right)$

${\text{cot}}^{-1}\left(45/28\right)=\theta ={\text{ cos}}^{-1}\left(45/53\right)$

${\text{cos}}^{-1}\left(0.849\right)\approx 31.89°={0.556}^c$

The angle of repose $\theta$ for the deicing salt $={\text{ cot}}^{-1}\left(r/h\right)={\text{ cot}}^{-1}\left(45/28\right)\approx 31.89°$.

To determine

To find:

B. The base diameter of the conical pile.

Answer to Problem 79AYU

Solution:

B. Diameter of the conical pile $=2\text{ x }27.3=54.6\text{ feet}$.

Explanation of Solution

Given:

The height of the conical pile $=17\text{ feet}$.

From 79 (a).

$\Theta =31.89°$

Formula used:

The angle of repose $\theta ={\text{ cot}}^{-1}\left(r/h\right)$.

Calculation:

$\text{cot}\theta =r/h=x/y$

Using the formula,

$1/\text{tan}\theta =r/h$

$\text{tan}\theta =h/r$

$\theta =31.89°,h=17\text{feet}$

$\text{tan}\left(31.89°\right)=17/r$

$r=17/\text{tan}\left(31.89°\right)$

$r=17/0.622=27.3\text{ feet}$

radius of the conical pile $\left(r\right)=27.3\text{ feet}$.

Diameter of the conical pile $=2\text{ x }27.3=54.6\text{ feet}$.

To determine

To find:

C. The height of conical pile of deicing salt.

Answer to Problem 79AYU

Solution:

C. Height of conical $\text{pile }\approx 38\text{ feet}$.

Explanation of Solution

Given:

The base diameter of conical pile $=122\text{ feet}$.

Radius of the conical pile $=61\text{ feet}$.

From 79 (a),

$\Theta =31.89°$

Formula used:

$\Theta ={\text{ cot}}^{-1}\left(r/h\right)$

$\text{cot}\theta =r/h$

Calculation:

$\text{cot}31.89°=61/h$

Using the formula,

$\text{cot}\theta =1/\text{tan}\theta$

$1/(\text{tan}\left(31.89°\right)=61/h$

$\text{tan}\left(31.89°\right)=h/61$

$h=61\text{ x tan}\left(31.89°\right)$

$h=61\text{ x }0.622=37.94\text{ feet} \approx 38\text{ feet}$

Height of conical pile $\approx 38\text{ feet}$.