
(a)
To graph: The function
(a)
Explanation of Solution
Given information:
The function
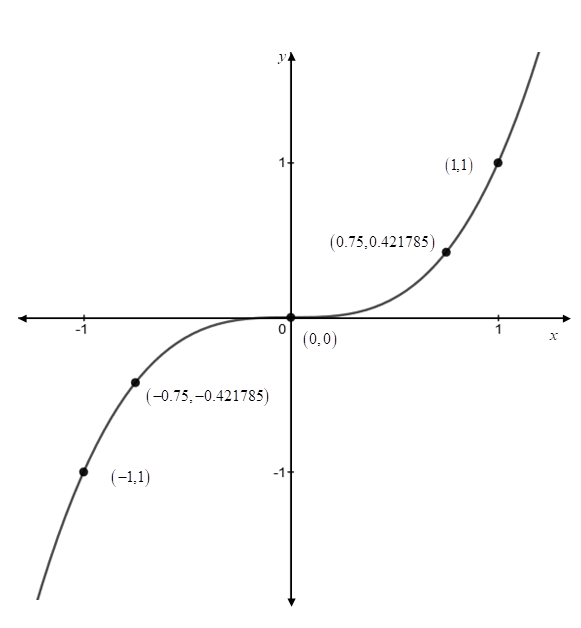
Graph:
For labelling, take three values of
The graph of the function
To find the inverse function
Now solve
Take the cube root of each side.
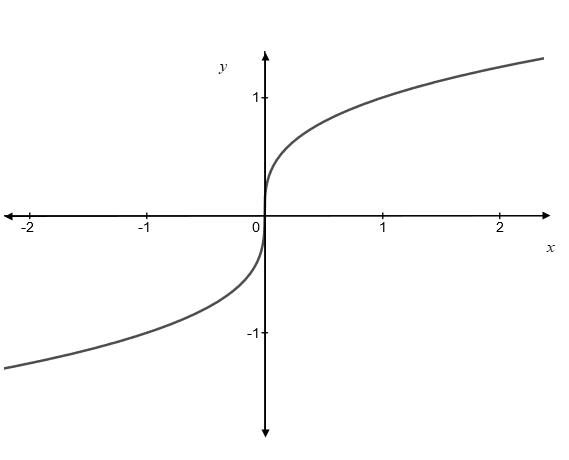
The inverse function of
The graph of the inverse function is a reflection about the line
Therefore, the graph of the inverse function
Interpretation:
The graph of
(b)
To graph: The function
(b)
Explanation of Solution
Given information:
The function,
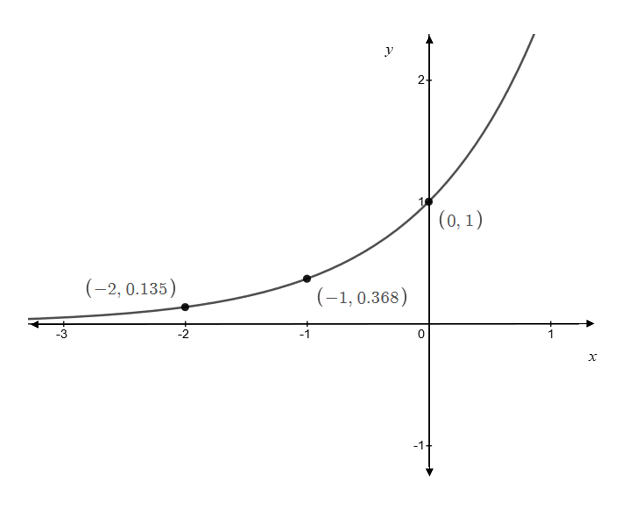
Graph:
For labelling, take three values of
The graph of the function
To find the inverse function
Now solve
Take log in both side.
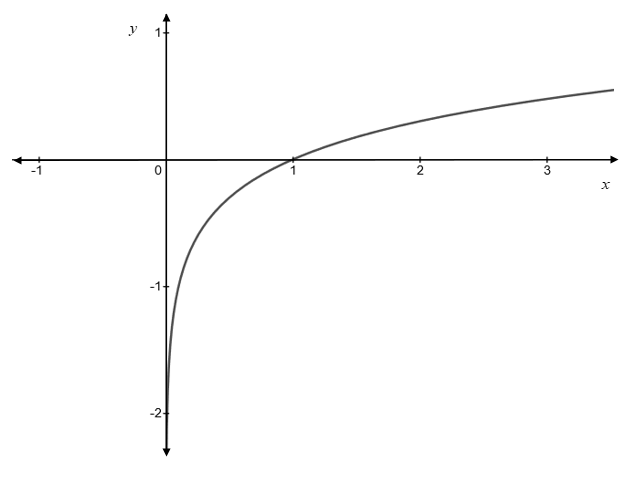
The inverse function of
As the graph of the inverse function is reflection about the line
Therefore, the graph of the inverse function
Interpretation:
The graph of
(c)
To graph: The function
(c)
Explanation of Solution
Given information:
The function,
Graph:
For labelling, take three values of
The graph of the function
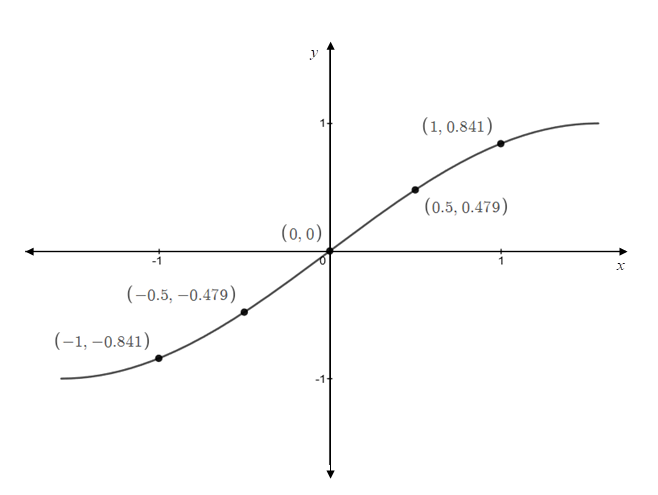
To find the inverse function
Now solve
The inverse function of
As the graph of the inverse function is a reflection about the line
Therefore, the graph of the inverse function
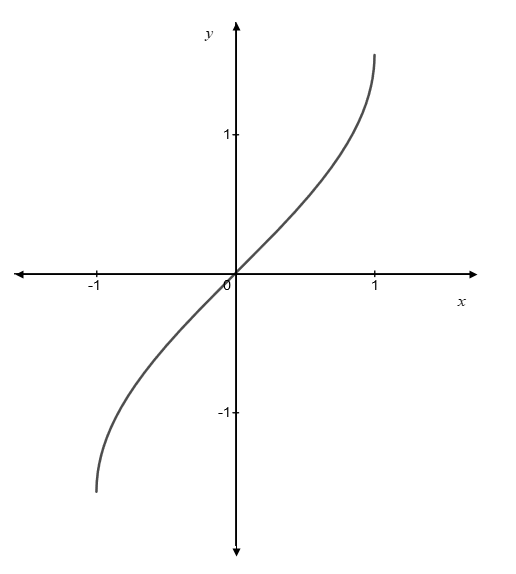
Interpretation:
The graph of
(d)
To graph: The function
(d)
Explanation of Solution
Given information:
The function,
Graph:
For labelling, take three values of
The graph of the function
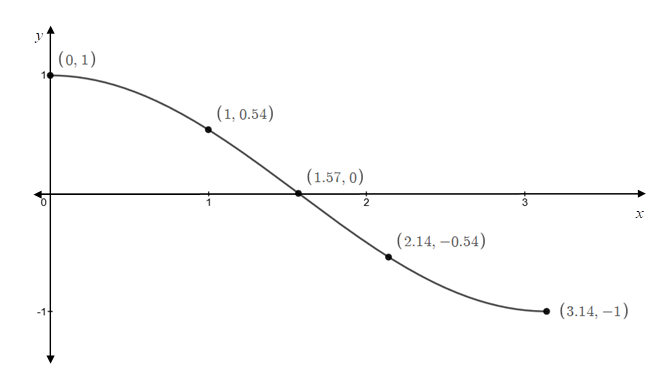
To find the inverse function
Now solve
The inverse function of
As the graph of the inverse function is a reflection about the line
Therefore, the graph of the inverse function
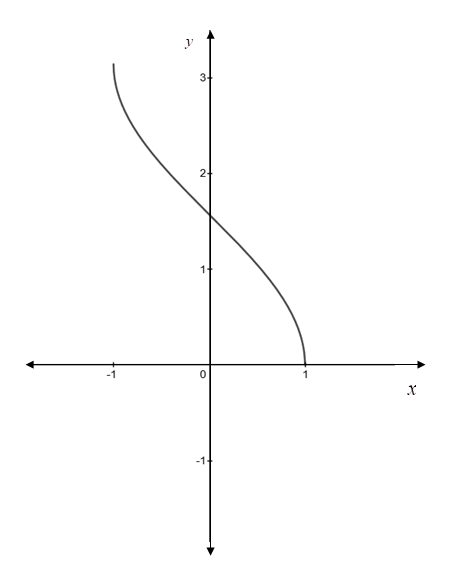
Interpretation:
The graph of
Chapter 7 Solutions
Precalculus
Additional Math Textbook Solutions
Pre-Algebra Student Edition
Calculus: Early Transcendentals (2nd Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Algebra and Trigonometry (6th Edition)
Introductory Statistics
University Calculus: Early Transcendentals (4th Edition)
- Evaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √ √(x + y) A R R = {(x, y) | 25 < x² + y² ≤ 36, x < 0} Hint: The integral and Region is defined in rectangular coordinates.arrow_forwardFind the volume of the solid that lies under the paraboloid z = 81 - x² - y² and within the cylinder (x − 1)² + y² = 1. A plot of an example of a similar solid is shown below. (Answer accurate to 2 decimal places). Volume using Double Integral Paraboloid & Cylinder -3 Hint: The integral and region is defined in polar coordinates.arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √4(1–2² 4(1 - x² - y²) dA R 3 R = {(r,0) | 0 ≤ r≤ 2,0π ≤0≤¼˜}. Hint: The integral is defined in rectangular coordinates. The Region is defined in polar coordinates.arrow_forward
- Evaluate the following integral over the Region R. (Answer accurate to 2 decimal places). R - 1 · {(r,0) | 1 ≤ r≤ 5,½π≤ 0<1π}. Hint: Be sure to convert to Polar coordinates. Use the correct differential for Polar Coordinates.arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √ √2(x+y) dA R R = {(x, y) | 4 < x² + y² < 25,0 < x} Hint: The integral and Region is defined in rectangular coordinates.arrow_forwardHW: The frame shown in the figure is pinned at A and C. Use moment distribution method, with and without modifications, to draw NFD, SFD, and BMD. B I I 40 kN/m A 3 m 4 marrow_forward
- Let the region R be the area enclosed by the function f(x)= = 3x² and g(x) = 4x. If the region R is the base of a solid such that each cross section perpendicular to the x-axis is an isosceles right triangle with a leg in the region R, find the volume of the solid. You may use a calculator and round to the nearest thousandth. y 11 10 9 00 8 7 9 5 4 3 2 1 -1 -1 x 1 2arrow_forwardLet the region R be the area enclosed by the function f(x) = ex — 1, the horizontal line y = -4 and the vertical lines x = 0 and x = 3. Find the volume of the solid generated when the region R is revolved about the line y = -4. You may use a calculator and round to the nearest thousandth. 20 15 10 5 y I I I | I + -1.5 -1 -0.5 0.5 1 1.5 2 2.5 3 -5 I -10 -15 I + I I T I I + -20 I + -25 I I I -30 I 3.5 4 xarrow_forwardplease show all the workarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





