
Concept explainers
(a)
To show: The gravitational potential energy of the person–Earth system as a function of the person’s variable height
(a)
Answer to Problem 78P
The gravitational potential energy of the person–Earth system as a function of the person’s variable height
Explanation of Solution
Given info: The mass of the person is
The acceleration due to gravity is
The expression for gravitational potential energy is as follows:
Here,
Substitute
Conclusion:
Therefore, the gravitational potential energy of the person–Earth system as a function of the person’s variable height
(b)
To show: Elastic potential energy of cord as a function of
(b)
Answer to Problem 78P
The elastic potential energy of cord as a function of
Explanation of Solution
Given info: The mass of the person is
The expression for elastic potential energy of spring is as follows:
The cord will stretch by length x only when the person falls more than the length of the cord. Now, the height of the balloon h should be more than the length of the cord l plus the person’s height y, for safe landing.
The expression for extension in spring is as follows:
Here,
Substitute
Substitute
Conclusion:
Therefore, the elastic potential energy of the cord as function of
(c)
To show: The total potential energy of the person-cord–Earth system as a function of
(c)
Answer to Problem 78P
The total potential energy of the person-cord–Earth system as a function of
Explanation of Solution
Given info: The mass of the person is
The expression for total potential energy of the person-cord–Earth system is as follows:
Substitute
Conclusion:
Therefore, the total potential energy of the person-cord–Earth system as a function of
(d)
To draw: The graph of gravitational, elastic, and total potential energies as a function of
(d)
Answer to Problem 78P
The graph of gravitational, elastic, and total potential energies as a function of
Explanation of Solution
Introduction:
The gravitational potential energy above the surface of the earth is directly proportional to the height of the object.
The elastic potential energy is proportional to the square of displacement.
The total potential energy is the sum of all the potential energies in the system.
Given info: The mass of the person is
From part (a), the expression for gravitational potential energy of person as a function of
Table for the above expression is shown below:
The graph of gravitational potential energy with displacement is shown below:
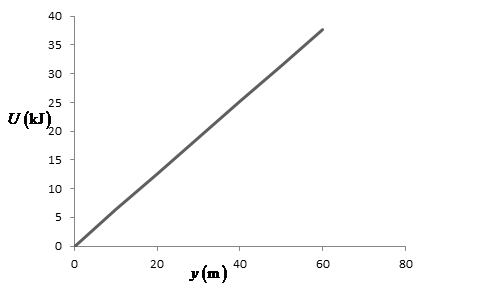
Figure(1)
From part (a), the expression for the elastic potential energy of cord as a function of
The value of elastic potential energy of the cord remains zero till the person does not fall
equal to the length of cord; therefore, the value of the above equation is zero for
Table for the above expression is shown below:
The graph of elastic potential energy with displacement is represented below:
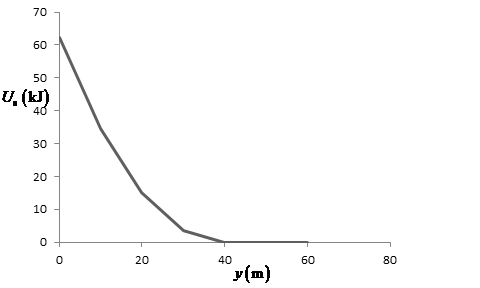
Figure(2)
From part (a), the expression for total potential energy of the person-cord–Earth system as a function of
When the value of
Table for the above expression is shown below:
The graph of total potential energy with displacement is represented below:
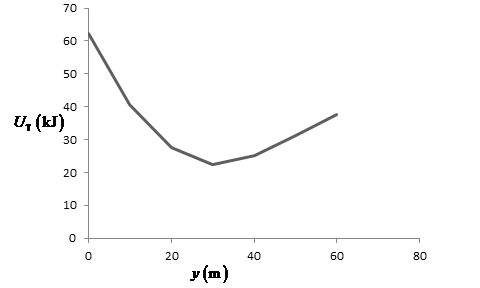
Figure(3)
(e)
The minimum height of the person above the ground during his plunge.
(e)
Answer to Problem 78P
The minimum height of the person above the ground during his plunge is
Explanation of Solution
Given info: The mass of the person is
The expression for change in total energy is as follows:
Here,
The value of initial kinetic energy is zero, as the person is at rest.
The length of cord is
Substitute
At minimum height above the ground during plunge, the person comes to rest and the change in kinetic energy is zero, as both values of initial and final kinetic energies are zero.
Substitute
The expression for the roots of the above quadratic equation is as follows:
Substitute
Conclusion:
Therefore, the minimum height of the person above the ground during his plunge is
(f)
Whether potential energy graph shows any equilibrium position and if so the elevation of equilibrium position, whether the equilibrium points are stable or unstable.
(f)
Answer to Problem 78P
The potential energy graph shows that in an equilibrium position at an elevation of
Explanation of Solution
Given info: The mass of the person is
The graph of potential energy shows the equilibrium position at the place where the value of total potential energy is minimum.
The expression for total potential energy is as follows:
Derive the above equation with the height of the person.
For the expression of minima, equate the above expression equal to zero.
The elevation at the point of equilibrium is
The person could not stop at the elevation of equilibrium position as he has kinetic energy that does not allow the person to stay at the elevation of equilibrium position. The equilibrium position is unstable.
Conclusion:
Therefore, the potential energy graph shows that in an equilibrium position at an elevation of
(g)
The jumper’s maximum speed.
(g)
Answer to Problem 78P
The jumper’s maximum speed is
Explanation of Solution
Given info: The mass of the person is
The expression for change in total energy is as follows:
Substitute
The initial kinetic energy of the jumper is zero; hence, the change in the kinetic energy equals the kinetic energy at that position. Velocity is directly proportional to the square root of the kinetic energy; therefore, for maximum value of kinetic energy, the velocity is maximum.
Differentiate the above expression with respect to
Equate
Substitute
Substitute
The height at which the velocity is maximum is
Substitute
Substitute
Substitute
Conclusion:
Therefore, the jumper’s maximum speed is
Want to see more full solutions like this?
Chapter 7 Solutions
Principles of Physics: A Calculus-Based Text
- Sketch the harmonic.arrow_forwardFor number 11 please sketch the harmonic on graphing paper.arrow_forward# E 94 20 13. Time a) What is the frequency of the above wave? b) What is the period? c) Highlight the second cycle d) Sketch the sine wave of the second harmonic of this wave % 7 & 5 6 7 8 * ∞ Y U 9 0 0 P 150arrow_forward
- Show work using graphing paperarrow_forwardCan someone help me answer this physics 2 questions. Thank you.arrow_forwardFour capacitors are connected as shown in the figure below. (Let C = 12.0 μF.) a C 3.00 με Hh. 6.00 με 20.0 με HE (a) Find the equivalent capacitance between points a and b. 5.92 HF (b) Calculate the charge on each capacitor, taking AV ab = 16.0 V. 20.0 uF capacitor 94.7 6.00 uF capacitor 67.6 32.14 3.00 µF capacitor capacitor C ☑ με με The 3 µF and 12.0 uF capacitors are in series and that combination is in parallel with the 6 μF capacitor. What quantity is the same for capacitors in parallel? μC 32.14 ☑ You are correct that the charge on this capacitor will be the same as the charge on the 3 μF capacitor. μCarrow_forward
- In the pivot assignment, we observed waves moving on a string stretched by hanging weights. We noticed that certain frequencies produced standing waves. One such situation is shown below: 0 ст Direct Measurement ©2015 Peter Bohacek I. 20 0 cm 10 20 30 40 50 60 70 80 90 100 Which Harmonic is this? Do NOT include units! What is the wavelength of this wave in cm with only no decimal places? If the speed of this wave is 2500 cm/s, what is the frequency of this harmonic (in Hz, with NO decimal places)?arrow_forwardFour capacitors are connected as shown in the figure below. (Let C = 12.0 µF.) A circuit consists of four capacitors. It begins at point a before the wire splits in two directions. On the upper split, there is a capacitor C followed by a 3.00 µF capacitor. On the lower split, there is a 6.00 µF capacitor. The two splits reconnect and are followed by a 20.0 µF capacitor, which is then followed by point b. (a) Find the equivalent capacitance between points a and b. µF(b) Calculate the charge on each capacitor, taking ΔVab = 16.0 V. 20.0 µF capacitor µC 6.00 µF capacitor µC 3.00 µF capacitor µC capacitor C µCarrow_forwardTwo conductors having net charges of +14.0 µC and -14.0 µC have a potential difference of 14.0 V between them. (a) Determine the capacitance of the system. F (b) What is the potential difference between the two conductors if the charges on each are increased to +196.0 µC and -196.0 µC? Varrow_forward
- Please see the attached image and answer the set of questions with proof.arrow_forwardHow, Please type the whole transcript correctly using comma and periods as needed. I have uploaded the picture of a video on YouTube. Thanks,arrow_forwardA spectra is a graph that has amplitude on the Y-axis and frequency on the X-axis. A harmonic spectra simply draws a vertical line at each frequency that a harmonic would be produced. The height of the line indicates the amplitude at which that harmonic would be produced. If the Fo of a sound is 125 Hz, please sketch a spectra (amplitude on the Y axis, frequency on the X axis) of the harmonic series up to the 4th harmonic. Include actual values on Y and X axis.arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





