Chapter 6.4, Problem 59STP

(a)

To determine

To find:the end behaviour of the graph.

Answer to Problem 59STP

  $\begin{array}{l}x\to \infty ;f\left(x\right)\to -\infty .\\ x\to -\infty ;f\left(x\right)\to -\infty .\end{array}$

Explanation of Solution

Given:

  

Concept used:

For an even degree function the end behaviour will be same direction.

For an odd degree function the end behaviour will be in different direction.

If $a>0$ .

Then curve will be open ward.

Or

The end point of the curve will be:

up and up for even.

Down and up for odd.

If $a<0$ .

Then curve will be down ward.

The end point of the curve will be:

Down and down for even.

Up and down for odd.

Calculation:

The curve equation is

  $y=a{x}^4+bx+c$ .

The degree is $4$ here and the end behaviour of the graph is:

End points lies on the same direction and there will be $5$ extreme value.

As

  $\begin{array}{l}x\to \infty .\\ f\left(x\right)\to -\infty .\\ x\to -\infty .\\ f\left(x\right)\to -\infty .\end{array}$

Hence, $\begin{array}{l}x\to \infty ;f\left(x\right)\to -\infty .\\ x\to -\infty ;f\left(x\right)\to -\infty .\end{array}$

(b)

To determine

To find:whether the graph represent even degree or an odd degree function.

Answer to Problem 59STP

The graph is even degree function.

Explanation of Solution

Given:

  

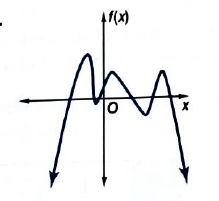
Concept used:

For an even degree function the end behaviour will be same direction.

For an odd degree function the end behaviour will be in different direction.

If number of cut in the x-axis or zeroes in the axis is even then the function is even degree function.

and if number of cut in the x-axis or zeroes in the axis is odd then the function is odd degree function.

Calculation:

According to the given:

Since the graph cut the x-axis at $6$ points so the graph will be even degree.

Hence, the graph is even degree function.

(c)

To determine

To find:the number of real zeroes in the graph.

Answer to Problem 59STP

There is $6$ zeroes.

Explanation of Solution

Given:

  

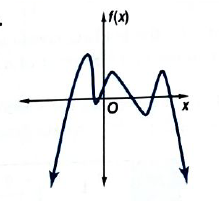
Concept used:

The number of real zeroes is the number of intersections with x-axis by the curve or number cut made by the curve on x-axis.

Calculation:

Zeroes can be calculated as the number of cut in the x-axis by curve.

Since there is $6$ cut in the x-axis by the curve.

Therefore, there will be $6$ zeroes.

Hence, there is $6$ zeroes.