Chapter 6.4, Problem 15PPS

(a)

To determine

To sketch: The graph of the function by making the table containing its value.

Answer to Problem 15PPS

The graph of the function is curve and it’s shown in graph above in green curve.

Explanation of Solution

Given:

  $\text{f}\left(\text{x}\right){\text{=-x}}^{\text{3}}\text{+2x}-4$ .

Concept used:

The graph of the function $\text{f}$ is the set of all point in the plane of the form $\left(\text{x,f}\left(\text{x}\right)\right)$ .

The graph can be defined by the graph of $\text{f}$ and the equation for the graph will be $\text{y=f}\left(\text{x}\right)$ .

The graph of the function is special case of the graph of an equation.

Calculation:

Table of values and graph.

Using different value of $\text{x}$ make a table in order to graph the polynomial function.

$\text{x}$	$\text{-2}$	$\text{-1}$	$\text{0}$	$\text{1}$	$\text{2}$
$\text{f}\left(\text{x}\right)$	$12$	$-1$	$-4$	$-3$	$\text{-4}$

The graph of the function $\text{f}\left(\text{x}\right){\text{=-x}}^{\text{3}}\text{+2x}-4$ will be:

  

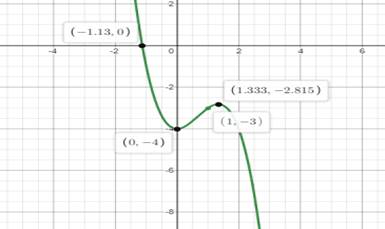
Hence, the graph of the function is curve and it’s shown in graph above in green curve.

(b)

To determine

To find: The consecutive integer value of x between the zeroes is located.

Answer to Problem 15PPS

The zeroes of the function lied at $\text{x=1}$ and $\text{x=2}$ .

Explanation of Solution

Given:

  $\text{f}\left(\text{x}\right){\text{=-x}}^{\text{3}}\text{+2x}-4$ .

Concept used:

The zeroes of the function resembled the function equates to zero.

  $\text{y=f}\left(\text{x}\right)\text{=0}$ .

The zero normally lies in between negative number and positive number.

Therefore, the consecutive number will negative approaches zero and positive approaches to zero except $\text{y=0}$ itself.

Calculation:

Table of values and graph.

Using different value of $\text{x}$ make a table in order to graph the polynomial function.

$\text{x}$	$\text{-2}$	$\text{-1}$	$\text{0}$	$\text{1}$	$\text{2}$
$\text{f}\left(\text{x}\right)$	$12$	$-1$	$-4$	$-3$	$\text{-4}$

The points in the graph so collected will form a graph for the given equation.

The changes in sign from the result indicates that there are zeroes between $\text{x=1}$ and $\text{x=2}$ .

Since, the sign of the function changes from negative to positive.

Hence the zeroes of the function lied at $\text{x=1}$ and $\text{x=2}$ .

(c)

To determine

To find: The Abscissa of the relative maxima and minima from the graph of the function.

Answer to Problem 15PPS

The relative maximum lied near $\text{x=0}$ and that of relative minima lied near $\text{x=1}$ .

Explanation of Solution

Given: $\text{f}\left(\text{x}\right){\text{=-x}}^{\text{3}}\text{+2x}-4$ .

Concept used:

Relative maxima:

Which is greater point than the points directly beside it at both sides.

Whereas,

Relative minimum:

Any point which is lesser than the points directly beside it at both sides.

Calculation:

The relative maxima and minima can be calculated as:

The value of $\text{f}\left(\text{x}\right)$ at $\text{x=0}$ greater than the surrounding points or the curve is open downward so there must be relative maximum near $\text{x=0}$ .

The value of $\text{f}\left(\text{x}\right)$ at $\text{x=1}$ is less than the surrounding points or the curve is open upward so there must be relative minimum near $\text{x=1}$ .

Hence relative maximum lied near $\text{x=0}$ and that of relative minima lied near $\text{x=1}$ .