Chapter 6.4, Problem 11CYU

To determine

To find: the consecutive value of x where the zeroes of the function is located and graph the function by collecting the domain and ranges.

Answer to Problem 11CYU

The relative maximum lied near $\text{x=2}\text{.387}$ and that of relative minima lied near $\text{x=0}\text{.279}$ and the zeroes of the function lied at $\text{x=0}$ and between $\left(-1,0\right)\cup \left(3,4\right)$ .

Explanation of Solution

Given:

  $\text{f}\left(\text{x}\right){\text{=-x}}^{\text{3}}{\text{+4x}}^{\text{2}}\text{-2x-1}$ .

Concept used:

The zeroes of the function resembled the function equates to zero.

  $\text{y=f}\left(\text{x}\right)\text{=0}$ .

The zero normally lies in between negative number and positive number.

Therefore, the consecutive number will negative approaches zero and positive approaches to zero except $\text{y=0}$ itself.

The graph of the function $\text{f}$ is the set of all point in the plane of the form $\left(\text{x,f}\left(\text{x}\right)\right)$ .

The graph can be defined by the graph of $\text{f}$ and the equation for the graph will be $\text{y=f}\left(\text{x}\right)$ .

The graph of the function is special case of the graph of an equation.

Relative maxima:

Which is greater point than the points directly beside it at both sides.

Whereas,

Relative minimum:

Any point which is lesser than the points directly beside it at both sides

Calculation:

The function is given as:

  $\text{f}\left(\text{x}\right){\text{=-x}}^{\text{3}}{\text{+4x}}^{\text{2}}\text{-2x-1}$ .

The table for the graph of the function will be:

Here,

the domain is $\text{x}$ and the value of $\text{y}$ is range.

$\text{x}$	$-4$	$-3$	$-2$	$\text{-1}$	$\text{0}$	$\text{1}$	$\text{2}$	$3$	$4$
$\text{f}\left(\text{x}\right)$	$135$	$68$	$27$	$6$	$-1$	$0$	$3$	$2$	$-9$

The points in the graph so collected will form a graph for the given equation.

The changes in sign from the result indicates that there are zeroes between $\text{x=-1}$ and $\text{x=0}$ and between $\text{x=3}$ and $\text{x=4}$ . One zero lied at $\text{x=1}$.

Since, the sign of the function changes from negative to positive.

The graph of the given equation $\text{f}\left(\text{x}\right){\text{=-3x}}^{\text{4}}{\text{+5x}}^{\text{3}}{\text{+4x}}^{\text{2}}\text{+4x-8}$ by collecting the points will be:

  

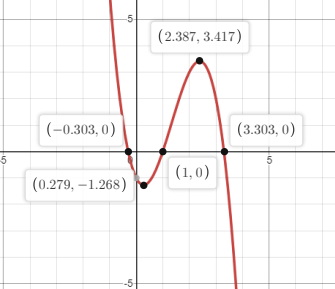
The relative maxima and minima can be calculated as:

The value of $\text{f}\left(\text{x}\right)$ at $\text{x=2}\text{.387}$ greater than the surrounding points or the curve is open downward so there must be relative maximum near $\text{x=2}\text{.387}$

The value of $\text{f}\left(\text{x}\right)$ at $\text{x=0}\text{.279}$ is less than the surrounding points or the curve is open upward so there must be relative minimum near $\text{x=0}\text{.279}$ .

Hence relative maximum lied near $\text{x=2}\text{.387}$ and that of relative minima lied near $\text{x=0}\text{.279}$ and the zeroes of the function lied at $\text{x=0}$ and between $\left(-1,0\right)\cup \left(3,4\right)$ .