Chapter 5.4, Problem 7PSA

a.

To determine

To find:The bases of isosceles trapezoid RSTV if

  $\overline{ST}$ is parallel to $\overline{RV}$ .

Answer to Problem 7PSA

The bases are $\overline{ST}$ and $\overline{RV}$ .

Explanation of Solution

Given:

In isosceles trapezoid RSTV, $\overline{ST}\parallel \overline{RV}$ .

Calculation:

  

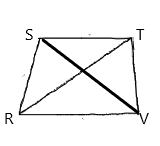
The below property is used:

In any isosceles trapezoid, two opposite sides (the bases) are parallel, and the other sides (the legs) are of equal length.

b.

To determine

To find: The diagonals of isosceles trapezoid RSTV if $\overline{ST}$ is parallel to $\overline{RV}$ .

Answer to Problem 7PSA

The diagonals are $\overline{SV}$ and $\overline{RT}$ .

Explanation of Solution

Given:

In isosceles trapezoid RSTV, $\overline{ST}\parallel \overline{RV}$ .

Calculation:

  

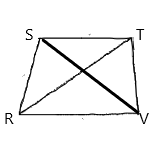
The below property is used:

A diagonal is a line segment joining two vertices of a polygon, when those vertices are not on same edge.

The diagonals of an isosceles trapezoid have the same length.

c.

To determine

To find: The legs of isosceles trapezoid RSTV if $\overline{ST}$ is parallel to $\overline{RV}$ .

Answer to Problem 7PSA

The legs are $\overline{SR}$ and $\overline{TV}$ .

Explanation of Solution

Given:

In isosceles trapezoid RSTV, $\overline{ST}\parallel \overline{RV}$ .

Calculation:

  

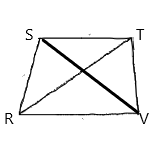
The below property is used:

In any isosceles trapezoid, two opposite sides (the bases) are parallel, and the other sides (the legs) are of equal length.

d.

To determine

To find: The lower base angles of isosceles trapezoid RSTV if $\overline{ST}$ is parallel to $\overline{RV}$ .

Answer to Problem 7PSA

The lower base angles are angle $SRV$ and angle $TVR$ .

Explanation of Solution

Given:

In isosceles trapezoid RSTV, $\overline{ST}\parallel \overline{RV}$ .

Calculation:

  

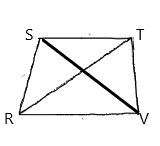
The below property is used:

In any isosceles trapezoid, two opposite sides (the bases) are parallel, and the other sides (the legs) are of equal length.

RV is lower base of an isosceles trapezoid RSTV.

The lower base angles are $\angle SRV$ and $\angle TVR$ .

e.

To determine

To find: The upper base angles of isosceles trapezoid RSTV if $\overline{ST}$ is parallel to $\overline{RV}$ .

Answer to Problem 7PSA

The upper base angles are angle $RST$ and angle $VTS$ .

Explanation of Solution

Given:

In isosceles trapezoid RSTV, $\overline{ST}\parallel \overline{RV}$ .

Calculation:

  

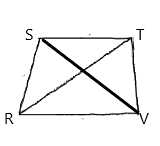
The below property is used:

In any isosceles trapezoid, two opposite sides (the bases) are parallel, and the other sides (the legs) are of equal length.

ST is upper base of an isosceles trapezoid RSTV.

The upper base angles are $\angle RST$ and $\angle VTS$ .

f.

To determine

To find: The pair of conjugate alternate angles of isosceles trapezoid RSTV if $\overline{ST}$ is parallel to $\overline{RV}$ .

Answer to Problem 7PSA

The conjugate alternate angles pair are angle $TSV$ congruent to angle $RVS$ and angle $STR$ congruent to angle $VRT$ .

Explanation of Solution

Given:

In isosceles trapezoid RSTV, $\overline{ST}\parallel \overline{RV}$ .

Calculation:

  

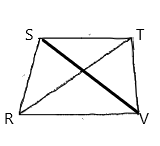
The below property is used:

Alternate angles are angles that are in opposite positions relative to a transversal intersecting two lines. If the alternate angles are between the two lines intersected by the transversal, they are called alternate interior angles. Conjugate angles are set of angles that sum to 360 degrees.

The conjugate alternate angles pair are $\angle TSV\cong \angle RVS$ and $\angle STR\cong \angle VRT$ .