
a.
To show: Diagonals
a.
Explanation of Solution
Given information:
The coordinates of point C are
The coordinates of point I are
The coordinates of point S are
The coordinates of point O are
Proof:
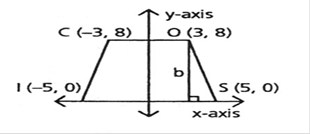
The coordinates of point Care
The coordinates of point S are
The coordinates of midpoints of
The coordinates of midpoints of
Diagonals
b.
To check:That Diagonals
b.
Answer to Problem 15PSC
Yes,diagonals
Explanation of Solution
Given information:
The coordinates of point C are
The coordinates of point I are
The coordinates of point S are
The coordinates of point O are
Formula used:
Slope of a line:
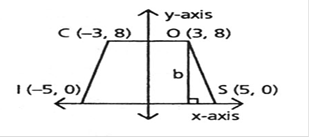
The coordinates of point C are
The coordinates of point S are
We now check the slopes of isosceles trapezoid CISO.
Slope of
The coordinates of point O are
The coordinates of point I are
Slope of
Since the product of slopes
c.
To Check:That the Diagonals of every isosceles trapezoid are perpendicular.
c.
Answer to Problem 15PSC
No, diagonals are not necessarily perpendicular.
Explanation of Solution
Given information:
The coordinates of point C are
The coordinates of point I are
The coordinates of point S are
The coordinates of point O are
Formula used:
Slope of a line:
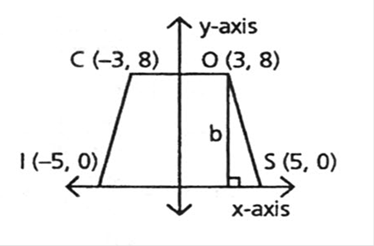
The coordinates of point C are
The coordinates of point S are
We now check the slopes of isosceles trapezoid CISO.
Slope of
The coordinates of point O are
The coordinates of point I are
Slope of
Since the product of slopes
If I and S are moved to
The coordinates of point C are
The coordinates of point S are
We now check the slopes of isosceles trapezoid CISO.
Slope of
The coordinates of point O are
The coordinates of point I are
Slope of
Since the product of slopes
d.
To find:The figure to draw to obtain a value of
d.
Answer to Problem 15PSC
The value of
Explanation of Solution
Given information:
The coordinates of point C are
The coordinates of point I are
The coordinates of point S are
The coordinates of point O are
Formula used:
The distance between two points by using the distance formula, which is an application of the Pythagoras theorem.
D
The below theorem is used:
Pythagoras theorem states that “In a right angled
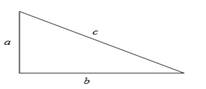
In right
Calculation:
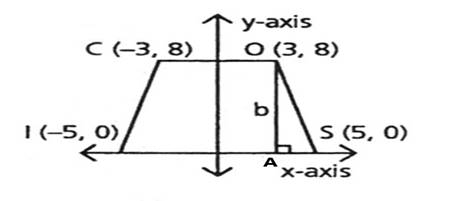
Draw b perpendicular to
The point A lies on x axis. Its y coordinate is 0.The x coordinate will be same as of x coordinate of point O.
The coordinates of point A are
The distance OA can be calculated by applying Pythagoras Theorem.
The distance AS can be calculated by applying Pythagoras Theorem.
In right angle triangle OAS, we get
Chapter 5 Solutions
Geometry For Enjoyment And Challenge
Additional Math Textbook Solutions
Elementary Statistics (13th Edition)
Introductory Statistics
College Algebra (7th Edition)
Elementary Statistics: Picturing the World (7th Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
- 18:36 G.C.A.2.ChordsSecantsandTa... จ 76 完成 2 In the accompanying diagram, AABC is inscribed in circle O, AP bisects BAC, PBD is tangent to circle O at B, and mZACB:m/CAB:m/ABC= 4:3:2 D B P F Find: mZABC, mBF, m/BEP, m/P, m/PBC ← 1 Őarrow_forward14:09 2/16 jmap.org 5G 66 In the accompanying diagram of circle O, diameters BD and AE, secants PAB and PDC, and chords BC and AD are drawn; mAD = 40; and mDC = 80. B E Find: mAB, m/BCD, m/BOE, m/P, m/PAD ← G.C.A.2.ChordsSecantsand Tangent s19.pdf (538 KB) + 4 保存... Xarrow_forward16:39 < 文字 15:28 |美图秀秀 保存 59% 5G 46 照片 完成 Bonvicino - Period Name: 6. A right regular hexagonal pyramid with the top removed (as shown in Diagram 1) in such a manner that the top base is parallel to the base of the pyramid resulting in what is shown in Diagram 2. A wedge (from the center) is then removed from this solid as shown in Diagram 3. 30 Diogram 1 Diegrom 2. Diagram 3. If the height of the solid in Diagrams 2 and 3 is the height of the original pyramid, the radius of the base of the pyramid is 10 cm and each lateral edge of the solid in Diagram 3 is 12 cm, find the exact volume of the solid in Diagram 3, measured in cubic meters. Show all work. (T 文字 贴纸 消除笔 涂鸦笔 边框 马赛克 去美容arrow_forward
- Answer question 4 pleasearrow_forward16:39 < 文字 15:28 |美图秀秀 保存 59% 5G 46 照片 完成 Bonvicino - Period Name: 6. A right regular hexagonal pyramid with the top removed (as shown in Diagram 1) in such a manner that the top base is parallel to the base of the pyramid resulting in what is shown in Diagram 2. A wedge (from the center) is then removed from this solid as shown in Diagram 3. 30 Diogram 1 Diegrom 2. Diagram 3. If the height of the solid in Diagrams 2 and 3 is the height of the original pyramid, the radius of the base of the pyramid is 10 cm and each lateral edge of the solid in Diagram 3 is 12 cm, find the exact volume of the solid in Diagram 3, measured in cubic meters. Show all work. (T 文字 贴纸 消除笔 涂鸦笔 边框 马赛克 去美容arrow_forwardAnswer question 3 pleasearrow_forward
- Answer question 3 pleasearrow_forward38 Below triangle is isosceles. Find the value of x. 70° 60° x 20° Warrow_forwardTo approximate the length of a marsh, a surveyor walks x = 400 meters from point A to point B. Then, the surveyor turns 75° and walks 220 meters to point C (see figure). Approximate the length AC of the marsh. (Round your answer to one decimal place.) m C B 75° 220 m x marrow_forward
- . The students who attend Memorial High School have a wide variety of extra-curricular activities to choose from in the after-school program. Students are 38% likely to join the dance team; 18% likely to participate in the school play; 42% likely to join the yearbook club; and 64% likely to join the marching band. Many students choose to participate in multiple activities. Students have equal probabilities of being freshmen, sophomores, juniors, or seniors.What is the probability of the union of being either a freshman or senior? 0.07 0.44 0.50 0.25arrow_forwardWhich angles are complementary to each other? Select all that apply. 3 2 4 in 5 1 Z1 and 23 Z1 and 25 22 and 23 Z2 and 25 Submitarrow_forwardWhich angles are adjacent to each other? Select all that apply. 3 2 4 67 5 8 11 10 12 12 9 27 and 28 Z9 and 12 Z3 and 24 Z10 and Z11arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

