Videos
a.
To find:The statement opposite sides of an isosceles trapezoid RTPAare congruent is true.
a.
Answer to Problem 3PSA
The statementopposite sides are congruent is false.
Explanation of Solution
Given information:
An isosceles trapezoidRTPA with sides RT, TP, PA and RA.
Diagonals oftrapezoid RTPA are RP and TA.
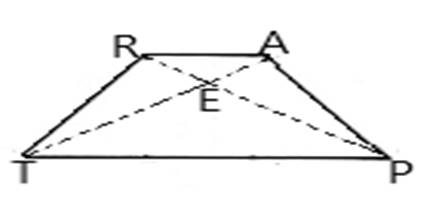
In any isosceles trapezoid, two opposite sides (the bases) are parallel, and the two other sides (the legs) are of equal lengths. The diagonals are of equal length. Only legs are congruent but bases are not congruent. Hence, the statement is false.
b.
To find: The statement opposite sides of an isosceles trapezoid RTPA are parallel is true.
b.
Answer to Problem 3PSA
The statement opposite sides are parallel is false.
Explanation of Solution
Given information:
An isosceles trapezoid RTPA with sides RT, TP, PA and RA.
Diagonals of trapezoid RTPA are RP and TA.
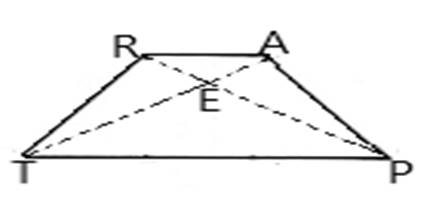
In any isosceles trapezoid, two opposite sides (the bases) are parallel, and the two other sides (the legs) are of equal lengths. The diagonals are of equal length. Only bases are parallel but legs are not parallel. Hence, the statement is false.
c.
To find:The statement diagonalsRP and TAof an isosceles trapezoid RTPAbisect the anglesis true.
c.
Answer to Problem 3PSA
The statement diagonals RP and TA bisect the
Explanation of Solution
Given information:
An isosceles trapezoid RTPA with sides RT, TP, PA and RA.
Diagonals of trapezoid RTPA are RP and TA.
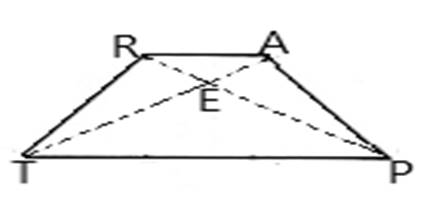
A diagonal doesn’t bisect angles in an isosceles trapezoid. It only happens in a square or a rhombus as there the length and breadth, both are equal.
d.
To find:The statement diagonals RP and TA of an isosceles trapezoid RTPA bisect each otheris true.
d.
Answer to Problem 3PSA
The statement diagonals RP and TA bisect each other is false.
Explanation of Solution
Given information:
An isosceles trapezoid RTPA with sides RT, TP, PA and RA.
Diagonals of trapezoid RTPA are RP and TA.
Isosceles trapezium is a trapezium whose non parallel sides are equal. If we have a quadrilateral whose diagonals bisect each other then it happens to be parallelogram. Every parallelogram is a trapezium but every trapezium is not parallelogram.
e.
To find:The statementdiagonals RP and TA of an isosceles trapezoid RTPAare congruentis true.
e.
Answer to Problem 3PSA
The statement diagonals RP and TAare congruent is true.
Explanation of Solution
Given information:
An isosceles trapezoid RTPA with sides RT, TP, PA and RA.
Diagonals of trapezoid RTPA are RP and TA.
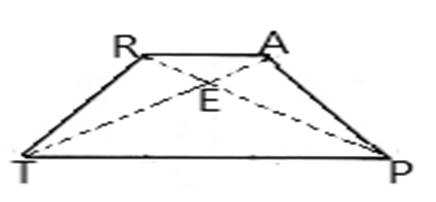
The diagonals of an isosceles trapezoid are also congruent, but they do not bisect each other. Isosceles trapezoid diagonals theorem states that “The diagonals of an isosceles trapezoid are congruent.
Chapter 5 Solutions
Geometry For Enjoyment And Challenge
Additional Math Textbook Solutions
University Calculus: Early Transcendentals (4th Edition)
Elementary Statistics
Thinking Mathematically (6th Edition)
Elementary Statistics: Picturing the World (7th Edition)
Pre-Algebra Student Edition
Elementary Statistics (13th Edition)
- из Review the deck below and determine its total square footage (add its deck and backsplash square footage together to get the result). Type your answer in the entry box and click Submit. 126 1/2" 5" backsplash A 158" CL 79" B 26" Type your answer here.arrow_forwardIn the graph below triangle I'J'K' is the image of triangle UK after a dilation. 104Y 9 CO 8 7 6 5 I 4 3 2 J -10 -9 -8 -7 -6 -5 -4 -3 -21 1 2 3 4 5 6 7 8 9 10 2 K -3 -4 K' 5 -6 What is the center of dilation? (0.0) (-5. 2) (-8. 11 (9.-3) 6- 10arrow_forwardSelect all that apply. 104 8 6 4 2 U U' -10 -8 -6 4 -2 2 4 6 10 -2 V' W' -4 -6 -8 -10 W V Select 2 correct answerts! The side lengths are equal in measure. The scale factor is 1/5. The figure has been enlarged in size. The center of dilation is (0.0) 8 10 Xarrow_forward
- In the graph below triangle I'J'K' is the image of triangle UK after a dilation. 104Y 9 CO 8 7 6 5 I 4 3 2 J -10 -9 -8 -7 -6 -5 -4 -3 -21 1 2 3 4 5 6 7 8 9 10 2 K -3 -4 K' 5 -6 What is the center of dilation? (0.0) (-5. 2) (-8. 11 (9.-3) 6- 10arrow_forwardQll consider the problem -abu+bou+cu=f., u=0 ondor I prove atu, ul conts. @ if Blu,v) = (b. 14, U) + ((4,0) prove that B244) = ((c- — ob)4;4) ③if c±vbo prove that acuius v. elliptic.arrow_forwardQ3: Define the linear functional J: H₁(2) R by ¡(v) = a(v, v) - L(v) Л Let u be the unique weak solution to a(u,v) = L(v) in H(2) and suppose that a(...) is a symmetric bilinear form on H(2) prove that 1- u is minimizer. 2- u is unique. 3- The minimizer J(u) can be rewritten under 1(u) = u Au-ub, algebraic form 1 2 Where A, b are repictively the stiffence matrix and the load vector Q4: A) Answer 1- show that the solution to -Au = f in A, u = 0 on a satisfies the stability Vullfll and show that ||V(u u)||||||2 - ||vu||2 2- Prove that Where lu-ul Chuz - !ull = a(u, u) = Vu. Vu dx + fu. uds B) Consider the bilinea forta Л a(u, v) = (Au, Av) (Vu, Vv + (Vu, v) + (u,v) Show that a(u, v) continues and V- elliptic on H(2)arrow_forward
- 7) In the diagram below of quadrilateral ABCD, E and F are points on AB and CD respectively, BE=DF, and AE = CF. Which conclusion can be proven? A 1) ED = FB 2) AB CD 3) ZA = ZC 4) ZAED/CFB E B D 0arrow_forward1) In parallelogram EFGH, diagonals EG and FH intersect at point I such that EI = 2x - 2 and EG = 3x + 11. Which of the following is the length of GH? a) 15 b) 28 c) 32 d) 56arrow_forward5) Which of the following are properties of all squares: 1. Congruent diagonals 2. Perpendicular diagonals 3. Diagonals that bisect vertex angles a) 1 and 2 only b) 1 and 3 only c) 2 and 3 only d) 1, 2, and 3arrow_forward
- 6) In an isosceles trapezoid HIJK it is known that IJ || KH. Which of the following must also be true? a) IJ = KH b) HIJK c) HIJK d) IJ KHarrow_forward4) When rectangle JKLM is plotted in the coordinate plane side JK has a slope equal to 3. What must be the slope of side MJ? a) 3/3 b) e 35 53 32 d) - 5arrow_forwardSolve for xarrow_forward
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning