
Applied Statics and Strength of Materials (6th Edition)
6th Edition
ISBN: 9780133840544
Author: George F. Limbrunner, Craig D'Allaird, Leonard Spiegel
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 5, Problem 5.7P
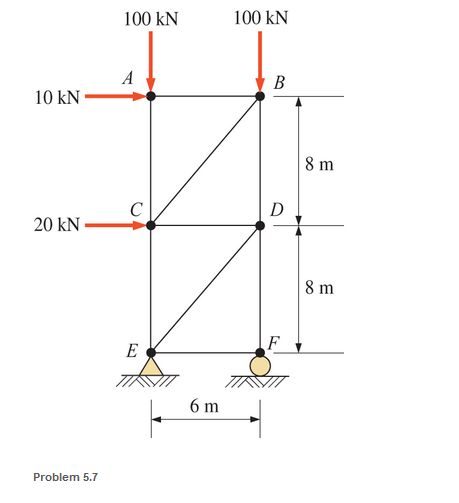
Calculate the forces in all members of the trusses shown, using the method of joints.
Expert Solution & Answer
Learn your wayIncludes step-by-step video

schedule06:49
Students have asked these similar questions
Calculate the principal stress σ1_at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m.
The following choices are provided in units of MPa and rounded to three decimal places.
Select one:
O 1.25745.455
O 2. 32181.818
3. 21454.545
4. 17163.636
5. 12872.727
Calculate the Von-Mises effective stress at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m.
The following choices are provided in units of MPa and rounded to three decimal places
Select one:
O 1.27870.272
O2. 18580.181
3. 11148.109
O 4. 14864.145
O 5.22296.218
A bar of length L and of a circular cross-section of diameter D is clamped at the top end and loaded at the other (bottom) end by a point load P as shown in Figure
Q2a. The cross-section of the bar is shown in Figure Q2b indicating that load is applied at the point A. The material used in the bar has specific weight y.
Find the magnitude and location of the maximum normal stress in the bar.
Figure Q2 a
Figure Q2 b
45°
Chapter 5 Solutions
Applied Statics and Strength of Materials (6th Edition)
Ch. 5 - through 5.7 Calculate the forces in all members of...Ch. 5 - Calculate the forces in all members of the trusses...Ch. 5 - Calculate the forces in all members of the trusses...Ch. 5 - Calculate the forces in all members of the trusses...Ch. 5 - Calculate the forces in all members of the trusses...Ch. 5 - Calculate the forces in all members of the trusses...Ch. 5 - Calculate the forces in all members of the trusses...Ch. 5 - Determine the forces in members CD, DH, and HI for...Ch. 5 - Determine the forces in members BC, BE, and FE for...Ch. 5 - Determine the forces in members BC, CH, and CG in...
Ch. 5 - For the Howe roof truss shown, determine the...Ch. 5 - Determine the forces in members DE, CE, and BC in...Ch. 5 - Calculate the forces in members BC, BG, and FG for...Ch. 5 - Determine the forces in members CD, BD, BE, and CB...Ch. 5 - A pin-connected A-frame supports a load, as shown....Ch. 5 - Determine the pin reactions at pins A, B, and C in...Ch. 5 - Calculate the pin reactions at each of the pins in...Ch. 5 - A bracket is pin connected at points A, B, and D...Ch. 5 - A pin-connected frame is loaded, as shown....Ch. 5 - The cylinder shown has a mass of 500 kg. Determine...Ch. 5 - A simple frame is pin connected at points A, B,...Ch. 5 - Using the method of sections, determine the forces...Ch. 5 - Using the method of sections, determine the forces...Ch. 5 - through 5.31 Calculate the forces in all members...Ch. 5 - Calculate the forces in all members of the trusses...Ch. 5 - Calculate the forces in all members of the trusses...Ch. 5 - Calculate the forces in all members of the trusses...Ch. 5 - Calculate the forces in all members of the trusses...Ch. 5 - Calculate the forces in all members of the trusses...Ch. 5 - Calculate the forces in all members of the trusses...Ch. 5 - Calculate the forces in all members of the trusses...Ch. 5 - For Problems 5.32 through 5.38, calculate the...Ch. 5 - For Problem 5.32 through 5.38, Calculate the...Ch. 5 - For Problems 5.32 through 5.38, calculate the...Ch. 5 - For Problems 5.32 through 5.38, calculate the...Ch. 5 - For Problem 5.32 through 5.38 , Calculate the...Ch. 5 - For Problems 5.32 through 5.38, calculate the...Ch. 5 - For Problems 5.32 through 5.38, calculate the...Ch. 5 - A pin-connected crane framework is loaded and...Ch. 5 - Calculate the pin reactions at pins A, B, and D in...Ch. 5 - Determine the pin reactions at pins A, B, and C in...Ch. 5 - The wall bracket shown is pin-connected at points...Ch. 5 - Calculate the pin reactions at each of the pins in...Ch. 5 - The A-frame shown is pin-connected at A,B,C, and...Ch. 5 - The tongs shown are used to grip an object. For an...Ch. 5 - A toggle joint is a mechanism by which a...Ch. 5 - In the toggle joint of Problem 5.46 , assume that...Ch. 5 -
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
A file that contains a Flash animation uses the __________ file extension. a. .class b. .swf c. .mp3 d. .flash
Web Development and Design Foundations with HTML5 (8th Edition)
How can user-defined operator overloading harm the readability of a program?
Concepts Of Programming Languages
T F All lines in a block should be indented one level.
Starting Out with C++ from Control Structures to Objects (9th Edition)
Employee and ProductionWorker Classes Design a class named Employee. The class should keep the following inform...
Starting Out with Java: From Control Structures through Data Structures (4th Edition) (What's New in Computer Science)
What is the metal removal rate in Problem 11 if the depth of cut is 6.35 mm 6.35mm14in.in.?
Degarmo's Materials And Processes In Manufacturing
What is pseudocode?
Starting Out With Visual Basic (8th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- A close end tube of thin-walled circular section may be subjected to torque Tand internal pressure P, as shown in Figure Q3. The shear stress in the wall caused by the torque can be calculated as σ = T/(2πR²t), where the mean radius of the cross section is R(i.e., the radius of the centreline of the wall) and the wall thickness is t. The internal radius of the tube can be calculated as (R-t/2). However, as R>> t, you can approximately assume that the internal radius of the tube is equal to Rin the subsequent calculation. The tube is made from a material with Young's modulus E, Poisson's ratio v. Orr T Ozz бее буг Z бее T бел Figure Q3 Centreline of the wall Rarrow_forwardA bar of length L and of a circular cross-section of diameter D is clamped at the top end and loaded at the other (bottom) end by a point load P as shown in Figure Q2a. The cross-section of the bar is shown in Figure Q2b indicating that load is applied at the point A. The material used in the bar has specific weight y. Find the magnitude and location of the maximum normal stress in the bar. Figure Q2 a Figure Q2 b 45° Aarrow_forward(If L=3508 mm, W-9189 N, E=80 GPa, Determine the deflection at the free end of the beam.) Step-4 Which equation in the following choices most accurately represents the functional relationship between the value of the deflection, Vmax ( Units: mm) at the free end (XL) of the beam and the second moment of area about z-axis, Izz (Units: mm²) of the cross section ? (Please note that " X = L/2" is the same as "X = L ÷ 2" .) Select one: O 1. Vmax 1776823249.026 / Izz O 2. Vmax 516518386.345/Izz O 3. Vmax=743786476.336/Izz O 4. Vmax 1002045669.509/Izz O 5. Vmax 330571767.261/Izz O 6. Vmax 196276986.811 / Izz O 7. Vmax 1435921114.038/Izzarrow_forward
- The second moment of area about z-axis of the cross section, Izz ( Units: mm4) can be calculated as Select one: O 1. 2.081 x 107 ○ 2. 2.281x 107 ○ 3. 2.201 x 107 ○ 4. 1.348x 107 ○ 5. 1.466 x107 ○ 6. 1.966x107 O 7. 1.833 x 107 O 8. 1.109x 107arrow_forward[(a) If the change of the diameter cannot exceed 0.1 m under elastic deformation, calculate the minimum allowable wall thickness of the cylindrical pressure vessel. (P=23.6 MPa, T=0 KN.m, R = 2 m, Young's modulus E = 246 GPa, and Poisson's ratio v = 0.21)] Step-3 The functional relationship between the change of the diameter, DD (units: mm), and wall thickness t(units: mm) can be most accurately expressed as Select one: O 1. DD-282.688/t O 2. DD=424.033/t O 3. DD=343.447/t 4. DD = 686.894/t O 5. DD=1696.130/t O 6. DD-228.965/t 7. DD=848.065/t 8. DD=1373.789/tarrow_forwardA bar of length L and of a circular cross-section of diameter D is clamped at the top end and loaded at the other (bottom) end by a point load P as shown in Figure Q2a. The cross-section of the bar is shown in Figure Q2b indicating that load is applied at the point A. The material used in the bar has specific weight y. Find the magnitude and location of the maximum normal stress in the bar. Z Figure Q2 a Figure Q2 b 45° Aarrow_forward
- A close end tube of thin-walled circular section may be subjected to torque Tand internal pressure P, as shown in Figure Q3. The shear stress in the wall caused by the torque can be calculated as T = T/(2πR²t), where the mean radius of the cross section is R(i.e., the radius of the centreline of the wall) and the wall thickness is t. The internal radius of the tube can be calculated as (R-t/2). However, as R>>t, you can approximately assume that the internal radius of the tube is equal to Rin the subsequent calculation. The tube is made from a material with Young's modulus E, Poisson's ratio v. T Centreline of the wall R P Ozz бөө Orr Z бут бее Ozz Figure Q3 (a) If the change of the diameter cannot exceed 0.1 m under elastic deformation, calculate the minimum allowable wall thickness of the cylindrical pressure vessel if P=23.6 MPa, T=0 KN.m, R = 2 m, Young's modulus E = 246 GPa, and Poisson's ratio v = 0.21. Step-1 the functional relationships between hoop stress σ and wall thickness…arrow_forwardA cantilever beam of a channel section and length L is loaded by a point load W applied at half-length of the beam through the centroid of the section, as shown in Figure Q1. The material of the beam is aluminum alloy with the Young’s modulus of E .arrow_forwardA bar of length L and of a circular cross-section of diameter D is clamped at the top end and loaded at the other (bottom) end by a point load P as shown in Figure Q2a. The cross-section of the bar is shown in Figure Q2b indicating that load is applied at the point A. The material used in the bar has specific weight y. Find the magnitude and location of the maximum normal stress in the bar. Figure Q2 a Figure Q2 b 45°arrow_forward
- Question2 The mission profile for a jet driven aircraft consists of the following segments: engine start and warm-up, taxi, take-off, climb to the cruise altitude of 35000 ft, descend to 10000 ft, one hour loiter at this altitude at 60% of the cruise speed, flight at loiter speed and altitude to an alternate airport (100 nm), descend to landing approach condition followed by the final landing, taxi and shutdown. The cruise Mach number is 0.8. No provisions are made for the reserved fuel or any trapped oil and fuel. The aircraft carries 200 people (including pilots and the cabin crew) at 175 lb each and 90 lb baggage each. This aircraft has a wing area of 2000 ft² a) If the landing stall speed of the aircraft is set at 100 kts corresponding to a landing weight of 0.85 Wro, and C(Lmax) Landing = 2.50, determine take-off weight and then calculate the range and empty weight of this aircraft (see Table Q2). Consider landing at sea level on a standard day. L/D at cruise L/D at 10000ft flight…arrow_forwardq Y X A ΕΙ L B Marrow_forwardIf L=3508 mm, W-9189 N, E=80 GPa, Determine the deflection at the free end of the beam. Step-1 The bend moment of the beam, M (Units: N.m), as a function of spatial coordinate X ( Units: m) can be described by Select one: O 1. M = 16117.506 +9189.000*X, for 0<=X<= L/2; M=0.00, for L/2< x <= L O 2. M = 16117506.000 - 9189.000*X, for 0<= x <= L/2; M = 9189.000* X, for L/2< x <= L O 3. M=16117.5069189.000*X, for 0<=X<= L/2; M=0.00, for L/2< x <= L O 4. M = 16117506.000 + 9189.000*X, for 0<=X<= L/2; M = 9189.000*X, for L/2arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L

International Edition---engineering Mechanics: St...
Mechanical Engineering
ISBN:9781305501607
Author:Andrew Pytel And Jaan Kiusalaas
Publisher:CENGAGE L
Engineering Basics - Statics & Forces in Equilibrium; Author: Solid Solutions - Professional Design Solutions;https://www.youtube.com/watch?v=dQBvQ2hJZFg;License: Standard YouTube License, CC-BY