Chapter 4.2, Problem 83AYU

In Problems 91-98, analyze each polynomial function using Steps 1 through 8 on page 193 in Section 4.1.

$f\left(x\right)=4x^5-8x^4-x+2$

[Hint: See Problem 67.]

To determine

To analyze: The polynomial function $f\left(x\right)=4x^5-8x^4-x+2$.

Answer to Problem 83AYU

$\text{The polynomial function }f\left(x\right)=4x^5-8x^4-x+2\text{ is analyzed}$.

Explanation of Solution

Given:

$f\left(x\right)=4x^5-8x^4-x+2$

Step 1: Determine the end behavior of the function

The polynomial function $f$ is of degree 5. The graph of $f$ behaves like $y=x^5$ for large values of $\left|x\right|$.

Step 2: Finding the $x$ and $y\text{-intercepts}$ of the graph of the function

To find the $y\text{-intercept}$, finding $f\left(0\right)$

$f\left(x\right)=4x^5-8x^4-x+2$

$f\left(0\right)=2$

$y\text{-intercept }=2$

To find the $x\text{-intercept}$, solving $f\left(x\right)=4x^5-8x^4-x+2=\text{ 0}$

Using synthetic division

$\left(x-2\right)\left(4x^4-1\right)=\left(x-2\right)\left(\sqrt{2x}+1\right)\left(\sqrt{2x}-1\right)\left(2x^2+1\right)$

$x\text{-intercept }=\text{ 2},\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}$

Step 3: Determining the zeros of the function and their multiplicity to find the graph crosses or touches the $x\text{-axis}$ at each intercept.

The zeros 2, $\frac{1}{\sqrt{2}}$ and $\frac{1}{\sqrt{2}}$ each have multiplicity 1. Therefore at 2, $\frac{1}{\sqrt{2}}$, $-\frac{1}{\sqrt{2}}$ the graph crosses the $x\text{-axis}$

Step 4: Using the graphing utility to graph the function.

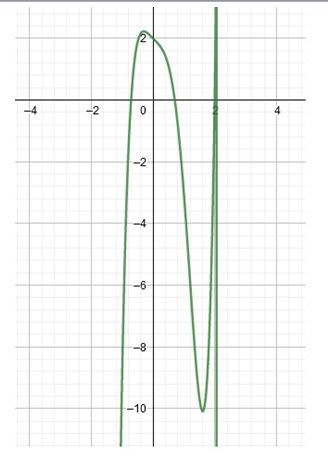
Step 5: Approximate the turning point of the graph

From the graph of $f$, we see $f$ has 3 turning points

Using the graph maximum turning point $=\left(-0.85,\text{ 2.15}\right)$ rounded to two decimal places

Using the graph minimum turning point $=\left(1.75,-10\right)$ rounded to two decimal places

Step 6: Redraw the graph

The graph passes through $\left(2,\text{ 0}\right)$ and $\left(-0.70,0\right)$

The end behavior of the graph $=y=x^5$

Step 7: Find the domain and range of the function

The domain and range is the set of all real numbers

Step 8: Use the graph to determine where the function is increasing or where it is decreasing

Based on the graph, $f$ is increasing on the intervals $\left(\infty ,-0.85\right]$ and $\left[1.8,2\right]$

Based on the graph, $f$ is decreasing $\left[-0.85,1.8\right]\left[2,\infty \right)$