Chapter 4.1, Problem 65AYU

To determine

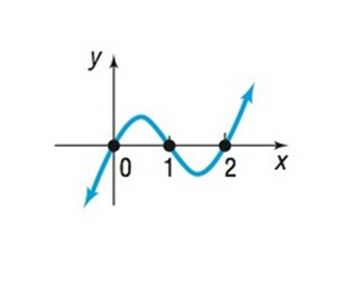
To construct: A polynomial function that will have the given graph.

Answer to Problem 65AYU

$\text{The polynomial function}f\left(x\right)=a\left(x-0\right)\left(x-1\right)\left(x-2\right)=x^3-3x^2+2x$.

Explanation of Solution

Given:

The given zeros from the graph $=0,1,2$.

There are 2 turning points. Therefore the least degree of the polynomial $=3$.

The graph crosses the $x\text{-axis}$ at $x=0,1,2$.

Therefore there will be odd multiplicity at $x=0,1,2$.

The polynomial function $f\left(x\right)=a\left(x-0\right)\left(x-1\right)\left(x-2\right)=x^3-3x^2+2x$.

Where $a$ is the leading coefficient and is non-zero real number causing a stretch, compression or reflection and not affecting the $x\text{-intercept}$ of the graph.