Chapter 4, Problem 9RE

To determine

To analyze : The polynomial function $f(x)={(x-2)}^2(x+4)$ .

Answer to Problem 9RE

The polynomial function $f(x)=x^3-12x+16$ .

The y -intercept is 16.

The x -intercept is zero 2 and -4.

Explanation of Solution

Given information:

  $f(x)={(x-2)}^2(x+4)$ .

Formula used:

The graph of a polynomial function $f(x)=a_n{x}^n+a_{n-1}{x}^{n-1}+\mathrm{...}+a_{1}x+a_0;a_n\ne 0$

Degree of a polynomial function $f:n$

Maximum number of turning points : $n-1$

At a zero even multiplicity: The graph of f touches the x -axis.

At a zero odd multiplicity : The graph of f crosses the x -axis.

For large $\left|x\right|$ , the graph of f behaves like the graph of $y=a_n{x}^n$ .

Calculation:

Consider ,

  $f(x)={(x-2)}^2(x+4)$

Step 1.

Re-writing the polynomial we have,

  $=f(x)=\left[x^2-2(x)(2)+4\right](x+4)$

  $\begin{array}{l}=\left[x^2-4x+4\right](x+4)\\ =x\left[x^2-4x+4\right]+4\left[x^2-4x+4\right]\\ =x^3-4x^2+4x+4x^2-16x+16\\ =x^3-12x+16\end{array}$

The polynomial function f is of degree 3. The graph of f behaves like $x^3$ .

Step 2.

The y −intercept :-

  $\begin{array}{l}=f(x)=x^3-12x+16\\ =f(0)=0-12(0)+16\\ =f(0)=16\end{array}$

The x -intercept :-

  $\begin{array}{l}=f(x)=0\\ =x^3-12x+16=0\\ ={(}^x(x+4)=0\\ =(x-2)(x-2)(x+4)=0\end{array}$

  $\begin{array}{l}(x-2)(x-2)=0\\ x=2,2\end{array}$ or $\begin{array}{l}x+4=0\\ x=-4\end{array}$

Step3.

The zeros of f are 2,2 and -4. The zero 2 is a zero of multiplicity 2, so the graph of f touches the x - axis at $x=2$ . The zero -4 is a zero of multiplicity 1, so the graph of f crosses the x -axis at $x=-4$ .

Step4.

Since the degree of polynomial function is 3. Therefore, the graph of the function will have at most $=3-1=2$ turning points.

Step5.

The x -intercept are 2, and -4.

The behavior of the graph of f near each x -intercept are as follows:-

Near $x=2$ ;

  $f(x)={(x-2)}^2(x+4)$

  $\begin{array}{l}={(}^x(2+4)\\ ={(}^x(6)\\ =6{(}^x\end{array}$

A parabola that opens up.

Near $x=-4$

  $f(x)={(x-2)}^2(x+4)$

  $\begin{array}{l}={(}^{-}(x+4)\\ ={(}^{-}(x+4)\\ =36(x+4)\\ =36x+144\end{array}$

The line with slope 36.

Step6.

Using Step1- Step5 graph is drawn showing the x - intercept and y -intercept. With the help of graph the behavior of each x −intercept can be observed.

  

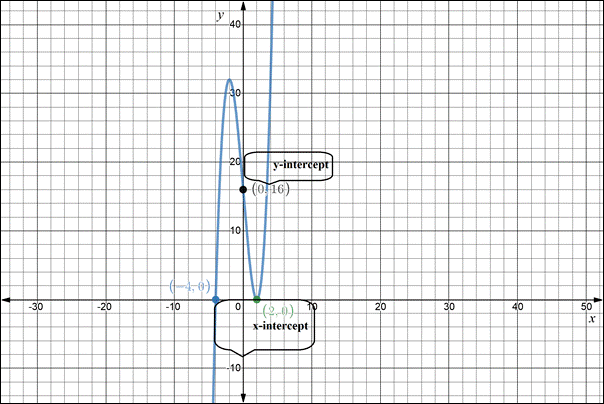
Figure1.

Hence , the polynomial function f has been analyzed.