
Bus and subway ridership for the summer months in London, England, is believed to be tied heavily to the number of tourists visiting the city. During the past 12 years, the data on the next page have been obtained:
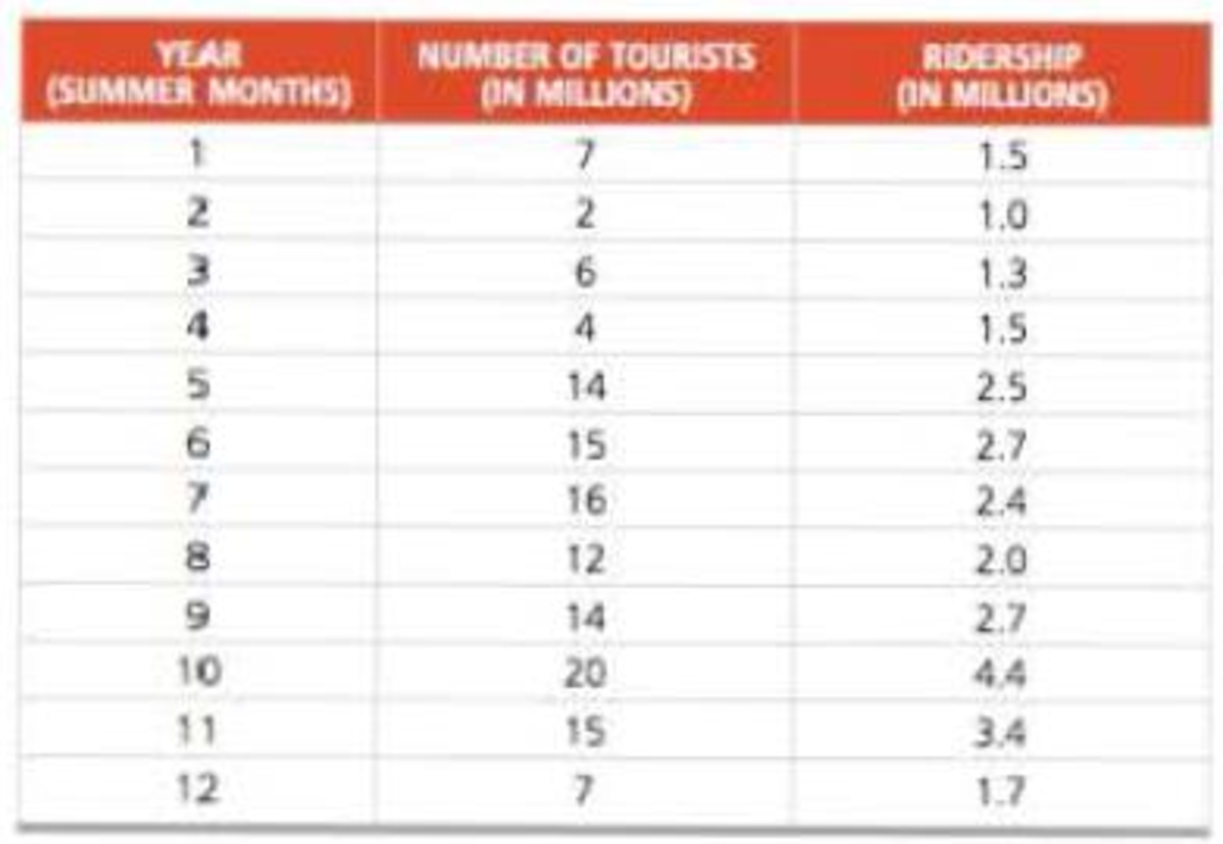
a) Plot these data and decide if a linear model is reasonable.
b) Develop a regression relationship.
c) What is expected ridership if 10 million tourists visit London in a year?
d) Explain the predicted ridership if there are no tourists at all.
e) What is the standard error of the estimate?
f) What is the model’s correlation coefficient and coefficient of determination?
a)
To determine: To plot the data and decide whether the linear model is reasonable.
Introduction: Forecasting is used to predict future changes or demand patterns. It involves different approaches and varies with different periods.
Answer to Problem 52P
The graph for the given data is plotted and it can be observed that the data points are scattered around.
Explanation of Solution
Given information:
| Year (Summer Months) | Number of tourist (in millions) | Ridership (in millions) |
| 1 | 7 | 1.5 |
| 2 | 2 | 1 |
| 3 | 6 | 1.3 |
| 4 | 4 | 1.5 |
| 5 | 14 | 2.5 |
| 6 | 15 | 2.7 |
| 7 | 16 | 2.4 |
| 8 | 12 | 2 |
| 9 | 14 | 2.7 |
| 10 | 20 | 4.4 |
| 11 | 15 | 3.4 |
| 12 | 7 | 1.7 |
Table 1
Graphical representation:
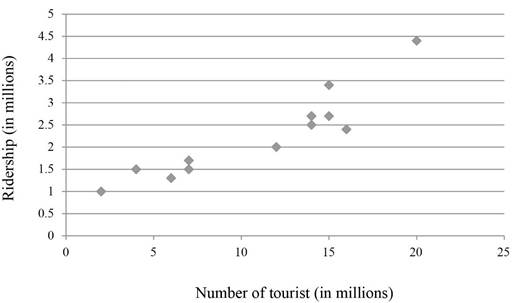
The data to plot the graph is taken from Table 1.
Hence, the graph for the given data is plotted and it can be observed that the data points are scattered around.
b)
To determine: A regression relationship.
Answer to Problem 52P
The linear regression equation is
Explanation of Solution
Given information:
| Year (Summer Months) | Number of tourist (in millions) | Ridership (in millions) |
| 1 | 7 | 1.5 |
| 2 | 2 | 1 |
| 3 | 6 | 1.3 |
| 4 | 4 | 1.5 |
| 5 | 14 | 2.5 |
| 6 | 15 | 2.7 |
| 7 | 16 | 2.4 |
| 8 | 12 | 2 |
| 9 | 14 | 2.7 |
| 10 | 20 | 4.4 |
| 11 | 15 | 3.4 |
| 12 | 7 | 1.7 |
Formula of least square regression:
Where,
Where,
| Year (Summer Months) | Number of tourist (in millions) (x) | Ridership (in millions) (y) | xy | x^2 | y^2 |
| 1 | 7 | 1.5 | 10.5 | 49 | 2.25 |
| 2 | 2 | 1 | 2 | 4 | 1 |
| 3 | 6 | 1.3 | 7.8 | 36 | 1.69 |
| 4 | 4 | 1.5 | 6 | 16 | 2.25 |
| 5 | 14 | 2.5 | 35 | 196 | 6.25 |
| 6 | 15 | 2.7 | 40.5 | 225 | 7.29 |
| 7 | 16 | 2.4 | 38.4 | 256 | 5.76 |
| 8 | 12 | 2 | 24 | 144 | 4 |
| 9 | 14 | 2.7 | 37.8 | 196 | 7.29 |
| 10 | 20 | 4.4 | 88 | 400 | 19.36 |
| 11 | 15 | 3.4 | 51 | 225 | 11.56 |
| 12 | 7 | 1.7 | 11.9 | 49 | 2.89 |
| Total | 132 | 27.1 | 352.9 | 1796 | 71.59 |
Table 2
Excel worksheet:
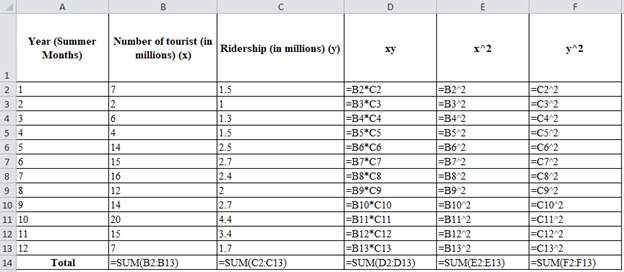
Substitute the values in the above formula.
Calculation of the average of x values
The average of x values is obtained by dividing the summation of x values with the number of periods n=12, the value of
Calculation of the average of y values
The average of y values is obtained by dividing the summation of sales with the number of periods n=12. The value of
Calculation ofthe slope of regression line‘b’:
The summation of the product of sales (y) with x values is ∑xy = 352.9, the product of number of period (n), the average of x values and the average of y values is obtained;
The summation of the square of x values, 1796, is subtracted from the product of the number of periods, 10with the average of x values, 11. The resultant value is 344. The slope of the regression line is obtained by dividing 1796 with 344. The value of ‘b’ is 0.159.
Calculation of the y-axis intercept ‘a’:
The y-axis intercept is obtained by the difference between the average of y values and values obtained by the product of the slope of regression line with the average of x values. The resultant value of ‘a’ is 0.511.
Least Square Regression forecasting equation:
Substitute the slope of regression line and they axis intercept in the regression equation which gives the liner regression equation for the data.
Hence, the linear regression equation is
c)
To determine: The expected ridership when 10 million tourists visit in a year.
Answer to Problem 52P
There is a 2.101 million ridership when 10 million tourists visit in a year.
Explanation of Solution
Given information:
| Year (Summer Months) | Number of tourist (in millions) | Ridership (in millions) |
| 1 | 7 | 1.5 |
| 2 | 2 | 1 |
| 3 | 6 | 1.3 |
| 4 | 4 | 1.5 |
| 5 | 14 | 2.5 |
| 6 | 15 | 2.7 |
| 7 | 16 | 2.4 |
| 8 | 12 | 2 |
| 9 | 14 | 2.7 |
| 10 | 20 | 4.4 |
| 11 | 15 | 3.4 |
| 12 | 7 | 1.7 |
Formula of least square regression:
Where,
Where,
Calculation of number of ridership when 10 million touristsvisit in a year:
Equation (1) provides the linear regression equation for the data and substitutes the number of tourists visiting in the regression equation. Substituting 10 million in the equation, the resultant value is found to be 2.101 million ridership.
Hence, there are 2.101 million ridership when 10 million touristsvisit in a year.
d)
To determine: The expected ridership when no tourists visit in a year.
Answer to Problem 52P
There is a 511,000 ridership when no touristsvisit in a year.
Explanation of Solution
Given information:
| Year (Summer Months) | Number of tourist (in millions) | Ridership (in millions) |
| 1 | 7 | 1.5 |
| 2 | 2 | 1 |
| 3 | 6 | 1.3 |
| 4 | 4 | 1.5 |
| 5 | 14 | 2.5 |
| 6 | 15 | 2.7 |
| 7 | 16 | 2.4 |
| 8 | 12 | 2 |
| 9 | 14 | 2.7 |
| 10 | 20 | 4.4 |
| 11 | 15 | 3.4 |
| 12 | 7 | 1.7 |
Formula of least square regression:
Where,
Where,
Calculation of the number of ridership when notouristsvisit in a year:
Equation (1) provides the linear regression equation for the data and substitutes the number of tourists visiting in the regression equation. Substituting 0 in the equation, the resultant value is 0.511 million ridership.
Hence, there is a 511,000 ridership when notouristsvisit in a year.
e)
To determine: The standard error of estimate.
Answer to Problem 52P
The standard error of estimate is0.4037.
Explanation of Solution
Given information:
| Year (Summer Months) | Number of tourists(in millions) | Ridership (in millions) |
| 1 | 7 | 1.5 |
| 2 | 2 | 1 |
| 3 | 6 | 1.3 |
| 4 | 4 | 1.5 |
| 5 | 14 | 2.5 |
| 6 | 15 | 2.7 |
| 7 | 16 | 2.4 |
| 8 | 12 | 2 |
| 9 | 14 | 2.7 |
| 10 | 20 | 4.4 |
| 11 | 15 | 3.4 |
| 12 | 7 | 1.7 |
Formula to compute the standard error of estimate:
Calculation of standard error of estimate:
The values to be substituted in the standard error of estimate formula are given inTable 2. Substitute the values from the table in the formula. This results in a standard error of estimate of 0.4037.
Hence, the standard error of estimate is 0.4037.
f)
To determine: The coefficient of correlation (r) and coefficient of determination (r2).
Answer to Problem 52P
The coefficient of correlation (r) and coefficient of determination (r2) are 717.41 & 0.840, respectively.
Explanation of Solution
Given information:
| Year (Summer Months) | Number of tourists(in millions) | Ridership (in millions) |
| 1 | 7 | 1.5 |
| 2 | 2 | 1 |
| 3 | 6 | 1.3 |
| 4 | 4 | 1.5 |
| 5 | 14 | 2.5 |
| 6 | 15 | 2.7 |
| 7 | 16 | 2.4 |
| 8 | 12 | 2 |
| 9 | 14 | 2.7 |
| 10 | 20 | 4.4 |
| 11 | 15 | 3.4 |
| 12 | 7 | 1.7 |
Formula to calculate the correlation coefficient:
Calculation of the correlation coefficient (r):
Table (2) provides the values to calculate the correlation coefficient (r).
Calculation of the correlation of determination (r2):
Hence, the coefficient of correlation and coefficient of determination are 717.41 and 0.840, respectively.
Want to see more full solutions like this?
Chapter 4 Solutions
EBK PRINCIPLES OF OPERATIONS MANAGEMENT
- EXPLAIN Human Resource Information System (HRIS)arrow_forwardRead the mini-case study below and answer the following questions.With an enormous amount of data stored in databases and data warehouses, it is increasinglyimportant to develop powerful tools for analysis of such data and mining interestingknowledge from it. Data mining is a process of inferring knowledge from such huge data. Themain problem related to the retrieval of information from the World Wide Web is theenormous number of unstructured documents and resources, i.e., the difficulty of locating andtracking appropriate sources.Briefly explain any five (5) types of information you can get from data mining.arrow_forwardProblem 1: Practice Problems Chapter 6 Managing Quality The accounts receivable department has documented the following defects over a 30-day period: Category Frequency Invoice amount does not agree with the check amount 108 Invoice not on record (not found) 24 No formal invoice issued Check (payment) not received on time 18 30 Check not signed 8 Invoice number and invoice referenced do not agree 12 What techniques would you use and what conclusions can you draw about defects in the accounts receivable department? Problem 2: Prepare a flow chart for purchasing a Big Mac at the drive-through window at McDonalds. Problem 3: Draw a fishbone chart detailing reasons why a part might not be correctly machined.arrow_forward
- Problem 5: Development of a new deluxe version of a particular software product is being considered. The activities necessary for the completion of this project are listed in the table below along with their costs and completion times in weeks. Activity Normal Crash Normal Crash Immediate Time Time Cost Cost Predecessor A 4 3 2,000 2,600 B 2 1 2,200 2,800 A C 3 3 500 500 A D 8 4 2,300 2,600 A E 6 3 900 1,200 B, D F 3 2 3,000 4,200 C, E G 4 2 1,400 2,000 F a. What is the project expected completion date? b. What is the total cost required for completing this project on normal time? c. If you wish to reduce the time required to complete this project by 1 week, which activity should be crashed, and how much will this increase the total cost?arrow_forwardI need answer typing clear urjent no chatgpt used pls i will give 5 Upvotes.with diagramarrow_forwardnot use ai pleasearrow_forward
- provide scholarly reseach and references for the following 1. explain operational risks and examples of such risk faced by management at financial institutions 2. discuss the importance of establishing an effective risk management policy at financial institutions to manage operational risk, giving example of a risk management strategy used by financial institutions to mitigate such risk. 3. what is the rold of the core principles of effective bank supervision as it relates to operational risk, in the effective management of financial institutions.arrow_forwardPlease show all units, work, and steps needed to solve this problem I need answer typing clear urjent no chatgpt used pls i will give 5 Upvotes.arrow_forwardIM.82 A distributor of industrial equipment purchases specialized compressors for use in air conditioners. The regular price is $50, however, the manufacturer of this compressor offers quantity discounts per the following discount schedule: Option Plan Quantity Discount A 1 - 299 0% B 300 - 1,199 0.50% C 1,200+ 1.50% The distributor pays $56 each time it places an order with the manufacturer. Holding costs are negligible (none) but they do earn 10% annual interest on all cash balances (meaning there will be a financial opportunity cost when they put cash into inventory). Annual demand is expected to be 10,750 units. When there is no quantity discount (Option Plan A, the first row of the schedule listed above), what is the adjusted order quantity? (Display your answer to the nearest whole number.) 491 Based on your answer to the previous question, and based on the annual demand as stated above, what will be the annual ordering costs? (Display your answer to the…arrow_forward
- Excel Please. The workload of many areas of banking operations varies considerably based on time of day. A variable capacity can be achieved effectively by employing part-time personnel. Because part-timers are not entitled to all the fringe benefits, they are often more economical than full-time employees. Other considerations, however, may limit the extent to which part-time people can be hired in a given department. The problem is to find an optimal workforce schedule that would meet personnel requirements at any given time and also be economical. Some of the factors affecting personnel assignments are listed here: The bank is open from 9:00am to 7:00pm. Full-time employees work for 8 hours (1 hour for lunch included) per day. They do not necessarily have to start their shift when the bank opens. Part-time employees work for at least 4 hours per day, but less than 8 hours per day and do not get a lunch break. By corporate policy, total part-time personnel hours is limited…arrow_forwardIM.84 An outdoor equipment manufacturer sells a rugged water bottle to complement its product line. They sell this item to a variety of sporting goods stores and other retailers. The manufacturer offers quantity discounts per the following discount schedule: Option Plan Quantity Price A 1 - 2,399 $5.50 B 2,400 - 3,999 $5.20 C 4,000+ $4.50 A large big-box retailer expects to sell 9,700 units this year. This retailer estimates that it incurs an internal administrative cost of $225 each time it places an order with the manufacturer. Holding cost for the retailer is $55 per case per year. (There are 40 units or water bottles per case.) Based on this information, and not taking into account any quantity discount offers, what is the calculated EOQ (in units)? (Display your answer to the nearest whole number.) Number Based on this information, sort each quantity discount plan from left to right by dragging the MOST preferred option plan to the left, and the LEAST preferred…arrow_forwardIn less than 150 words, what is an example of what your reflection of core values means to you and your work: Commitment, Perseverance, Community, Service, Pride?arrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,MarketingMarketingISBN:9780357033791Author:Pride, William MPublisher:South Western Educational Publishing
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,MarketingMarketingISBN:9780357033791Author:Pride, William MPublisher:South Western Educational Publishing Contemporary MarketingMarketingISBN:9780357033777Author:Louis E. Boone, David L. KurtzPublisher:Cengage Learning
Contemporary MarketingMarketingISBN:9780357033777Author:Louis E. Boone, David L. KurtzPublisher:Cengage Learning Purchasing and Supply Chain ManagementOperations ManagementISBN:9781285869681Author:Robert M. Monczka, Robert B. Handfield, Larry C. Giunipero, James L. PattersonPublisher:Cengage Learning
Purchasing and Supply Chain ManagementOperations ManagementISBN:9781285869681Author:Robert M. Monczka, Robert B. Handfield, Larry C. Giunipero, James L. PattersonPublisher:Cengage Learning




