Chapter 4, Problem 13P

At you can see in the following table, demand for heart transplant surgery at Washington General Hospital has increased steadily in the past few years:

The director of medical services predicted 6 years ago that demand in year 1 would be 41 surgeries.

a) Use exponential smoothing, first with a smoothing constant of .6 and then with one of .9, to develop forecasts for years 2 through 6.

b) Use a 3-year moving average to forecast demand in years 4, 5, and 6.

c) Use the trend-projection method to forecast demand in years 1 through 6.

d) With MAD as the criterion, which of the four forecasting methods is best?

Summary Introduction

To determine: Findthe forecast for years 2 through 6, using exponential smoothing.

Introduction: A sequence of data pointing in successive order is known as time series. Time series forecasting is the prediction based on past events which are at a uniform time interval. Moving average method and trend projections are one of the time series methods which use weights to prioritize past data.

Answer to Problem 13P

The forecast for years 2 through 6 using exponential smoothing with smoothing constant 0.6 is 56.263 and smoothing constant 0.9 is 57.757.

Explanation of Solution

Forecast for years 1 through 6 using exponential smoothing with smoothing constant 0.6:

Given information:

Year	1	2	3	4	5	6
Heart Transplants	45	50	52	56	58

$\begin{array}{c}\text{Initial forecast for year 1}=41\\ \text{Smoothing}\text{constant}=\text{0}\text{.6}\end{array}$

Formula to calculate the forecasted demand:

${\text{F}}_{\text{t}}={\text{F}}_{\text{t-1}}+\text{α}\left({\text{A}}_{\text{t-1}}-{\text{F}}_{\text{t-1}}\right)$

Where,

$\begin{array}{c}{\text{F}}_{\text{t}}=\text{new}\text{forecast}\\ {\text{F}}_{\text{t-1}}=\text{Previous}\text{period's}\text{forecast}\\ \text{α}=\text{smoothing}\text{constant}\\ {\text{A}}_{\text{t-1}}=\text{Previous}\text{period}\text{actual}\text{Demand}\end{array}$

Smoothing constant=0.6
Year	Heart Transplants	Forecast	Absolute error
1	45	41	4.000
2	50	43.400	6.600
3	52	47.360	4.640
4	56	50.144	5.856
5	58	53.658	4.342
6		56.263
		Total	25.438
		MAD	5.08768

Excel worksheet:

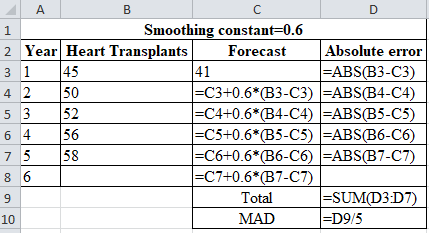
Calculation of the forecast for year 2:

$\begin{array}{c}{\text{F}}_2={\text{F}}_1+\text{α}\left({\text{A}}_1-{\text{F}}_1\right)\\ =41+0.6\left(45-41\right)\\ =43.40\end{array}$

To calculate forecast for year 2, substitute the value of forecast of year 1, smoothing constant and difference of actual and forecasted demand in the above formula. The result of the forecast for year 2 is 43.40.

Calculation of the forecast for year 3:

$\begin{array}{c}{\text{F}}_3={\text{F}}_2+\text{α}\left({\text{A}}_2-{\text{F}}_2\right)\\ =43.40+0.6\left(50-43.40\right)\\ =47.360\end{array}$

To calculate forecast for year 3, substitute the value of forecast of year 2, smoothing constant and difference of actual and forecasted demand in the above formula. The result of the forecast for year 3 is 47.360.

Calculation of the forecast for year 4:

$\begin{array}{c}{\text{F}}_4={\text{F}}_3+\text{α}\left({\text{A}}_3-{\text{F}}_3\right)\\ =47.360+0.6\left(52-47.360\right)\\ =50.144\end{array}$

To calculate forecast for year 4, substitute the value of forecast of year 3, smoothing constant and difference of actual and forecasted demand in the above formula. The result of the forecast for year 4 is 50.144.

Calculation of the forecast for year 5:

$\begin{array}{c}{\text{F}}_5={\text{F}}_4+\text{α}\left({\text{A}}_4-{\text{F}}_4\right)\\ =50.144+0.6\left(56-50.144\right)\\ =53.658\end{array}$

To calculate forecast for year 5, substitute the value of forecast of year 4, smoothing constant and difference of actual and forecasted demand in the above formula. The result of the forecast for year 5 is 53.658.

Calculation of the forecast for year 6:

$\begin{array}{c}{\text{F}}_6={\text{F}}_5+\text{α}\left({\text{A}}_5-{\text{F}}_5\right)\\ =53.658+0.6\left(58-53.658\right)\\ =56.263\end{array}$

To calculate forecast for year 6, substitute the value of forecast of year 5, smoothing constant and difference of actual and forecasted demand in the above formula. The result of the forecast for year 6 is 56.263.

Calculation of MAD using exponential smoothing with smoothing constant α=0.6:

Formula to calculate the Mean Absolute Deviation:

$\text{MAD}=\frac{{\displaystyle \sum \left|\text{Actual}-\text{Forecast}\right|}}{n}$

Calculation of the absolute error for year 1:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|45-41\right|\\ =\left|4\right|\\ =4\end{array}$

The absolute error for year 1 is the modulus of the difference between 45 and 41, which corresponds to 4. Therefore, the absolute error for year 1 is 4.

Calculation of the absolute error for year 2:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|50-43.4\right|\\ =\left|6.6\right|\\ =6.6\end{array}$

The absolute error for year 2 is the modulus of the difference between 50 and 43.4, which corresponds to 6.6. Therefore, the absolute error for year 2 is 6.6.

Calculation of the absolute error for year 3:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|52-47.360\right|\\ =\left|4.640\right|\\ =4.640\end{array}$

The absolute error for year 3 is the modulus of the difference between 52 and 47.360, which corresponds to 4.640. Therefore, the absolute error for year 3 is4.640.

Calculation of the absolute error for year 4:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|56-50.144\right|\\ =\left|5.856\right|\\ =5.856\end{array}$

The absolute error for year 4 is the modulus of the difference between 56 and 50.144, which corresponds to 5.856. Therefore, the absolute error for year 4 is5.856.

Calculation of the absolute error for year 5:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|58-53.658\right|\\ =\left|4.342\right|\\ =4.342\end{array}$

The absolute error for year 5 is the modulus of the difference between 58 and 53.658, which corresponds to 4.342. Therefore, the absolute error for year 5 is 4.342.

Calculation of the Mean Absolute Deviation using exponential smoothing:

$\begin{array}{c}\text{MAD}=\frac{{\displaystyle \sum \left|\text{Actual}-\text{Forecast}\right|}}{n}\\ =\frac{4.0+6.6+4.640+5.856+4.342}{5}\\ =\frac{25.438}{5}\\ =5.08768\end{array}$ (1)

Upon the substitution of summation value of absolute error for 5 years, that is, 25.438 are divided by number of years. That is, 5 yields MAD of 5.08768.

The forecast for years 2 through 6 using exponential smoothing with 0.6 as smoothing constant is 56.263.

The forecast for years 1 through 6 using exponential smoothing with smoothing constant 0.9:

Given information:

Year	1	2	3	4	5	6
Heart Transplants	45	50	52	56	58

$\begin{array}{c}\text{Initial forecast for year 1}=41\\ \text{Smoothing}\text{constant}=\text{0}\text{.9}\end{array}$

Formula to calculate the forecasted demand:

${\text{F}}_{\text{t}}={\text{F}}_{\text{t-1}}+\text{α}\left({\text{A}}_{\text{t-1}}-{\text{F}}_{\text{t-1}}\right)$

Where

$\begin{array}{c}{\text{F}}_{\text{t}}=\text{new}\text{forecast}\\ {\text{F}}_{\text{t-1}}=\text{Previous}\text{period's}\text{forecast}\\ \text{α}=\text{smoothing}\text{constant}\\ {\text{A}}_{\text{t-1}}=\text{Previous}\text{period}\text{actual}\text{Demand}\end{array}$

Smoothing constant=0.9
Year	Heart Transplants	Forecast	Absolute Error
1	45	41	4
2	50	44.600	5.400
3	52	49.460	2.540
4	56	51.746	4.254
5	58	55.575	2.425
6		57.757	57.757
		Total	18.6194
		MAD	3.72388

Excel worksheet:

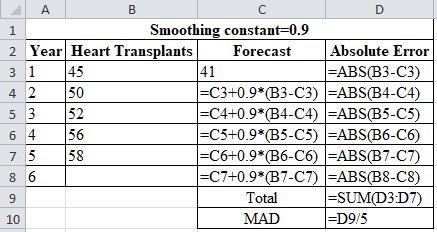
Calculation of the forecast for year 2:

$\begin{array}{c}{\text{F}}_2={\text{F}}_1+\text{α}\left({\text{A}}_1-{\text{F}}_1\right)\\ =41+0.9\left(45-41\right)\\ =44.60\end{array}$

To calculate the forecast for year 2, substitute the value of forecast of year 1, smoothing constant and difference of actual and forecasted demand in the above formula. The result of the forecast for year 2 is 44.60.

Calculation of the forecast for year 3:

$\begin{array}{c}{\text{F}}_3={\text{F}}_2+\text{α}\left({\text{A}}_2-{\text{F}}_2\right)\\ =43.40+0.9\left(50-44.60\right)\\ =49.460\end{array}$

To calculate forecast for year 3, substitute the value of forecast of year 2, smoothing constant and difference of actual and forecasted demand in the above formula. The result of the forecast for year 3 is 49.460.

Calculation of the forecast for year 4:

$\begin{array}{c}{\text{F}}_4={\text{F}}_3+\text{α}\left({\text{A}}_3-{\text{F}}_3\right)\\ =49.460+0.9\left(52-49.460\right)\\ =51.746\end{array}$

To calculate forecast for year 4, substitute the value of forecast of year 3, smoothing constant and difference of actual and forecasted demand in the above formula. The result of the forecast for year 4 is 50.144.

Calculation of the forecast for year 5:

$\begin{array}{c}{\text{F}}_5={\text{F}}_4+\text{α}\left({\text{A}}_4-{\text{F}}_4\right)\\ =51.746+0.9\left(56-51.746\right)\\ =55.575\end{array}$

To calculate forecast for year 5, substitute the value of forecast of year 4, smoothing constant and difference of actual and forecasted demand in the above formula. The result of the forecast for year 5 is55.575.

Calculation of the forecast for year 6:

$\begin{array}{c}{\text{F}}_6={\text{F}}_5+\text{α}\left({\text{A}}_5-{\text{F}}_5\right)\\ =55.575+0.9\left(58-55.575\right)\\ =57.757\end{array}$

To calculate forecast for year 6, substitute the value of forecast of year 5, smoothing constant and difference of actual and forecasted demand in the above formula. The result of the forecast for year 6 is57.757.

Calculation of MAD using exponential smoothing with smoothing constant α=0.9:

Formula to calculate the Mean Absolute Deviation:

$\text{MAD}=\frac{{\displaystyle \sum \left|\text{Actual}-\text{Forecast}\right|}}{n}$

Calculation of the absolute error for year 1:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|45-41\right|\\ =\left|4\right|\\ =4\end{array}$

The absolute error for year 1 is the modulus of the difference between 45 and 41, which corresponds to 4. Therefore, the absolute error for year 1 is 4.

Calculation of the absolute error for year 2:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|50-44.6\right|\\ =\left|5.4\right|\\ =5.4\end{array}$

The absolute error for year 2 is the modulus of the difference between 50 and 44.6, which corresponds to 5.4. Therefore, the absolute error for year 2 is 5.4.

Calculation of the absolute error for year 3:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|52-49.460\right|\\ =\left|2.540\right|\\ =2.540\end{array}$

The absolute error for year 3 is the modulus of the difference between 52 and49.460, which corresponds to 2.540. Therefore, the absolute error for year 3 is2.540.

Calculation of the absolute error for year 4:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|56-51.746\right|\\ =\left|4.254\right|\\ =4.254\end{array}$

The absolute error for year 4 is the modulus of the difference between 56 and51.746, which corresponds to 4.254. Therefore, the absolute error for year 4 is4.254.

Calculation of the absolute error for year 5:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|58-55.575\right|\\ =\left|2.425\right|\\ =2.425\end{array}$

The absolute error for year 5 is the modulus of the difference between 58 and55.575, which corresponds to 2.425. Therefore, the absolute error for year 5 is 2.425.

Calculation of the Mean Absolute Deviation using exponential smoothing:

$\begin{array}{c}\text{MAD}=\frac{{\displaystyle \sum \left|\text{Actual}-\text{Forecast}\right|}}{n}\\ =\frac{4.0+5.4+2.54+4.254+2.425}{5}\\ =\frac{18.6194}{5}\\ =3.72388\end{array}$ (2)

Upon the substitution of summation value of absolute error for 5 years, that is,18.6194are divided by the number of years. That is, 5 yields MAD of 3.72388.

The forecast for years 2 through 6 using exponential smoothing with 0.9 as smoothing constant is 57.757.

Hence, the forecast for years 2 through 6 using exponential smoothing with smoothing constant 0.6 is 56.263 and smoothing constant 0.9 is 57.757.

Summary Introduction

To determine: Using 3-year moving average, forecast the demand for years 4, 5 and 6.

Answer to Problem 13P

The demand forecast for years 4, 5 and 6 is 49, 52.67 and 55.33.

Explanation of Solution

Given information:

Year	1	2	3	4	5	6
Heart Transplants	45	50	52	56	58

Formula to calculate the forecasted demand:

$\text{Moving}\text{average=}\frac{{\displaystyle \sum \text{demand}\text{in}\text{previous}n\text{periods}}}{n}$

Year	Heart Transplants	Forecast	Absolute Error
1	45
2	50
3	52
4	56	49	7
5	58	52.67	5.333
6		55.33
		Total	12.333
		MAD	6.1667

Excel worksheet:

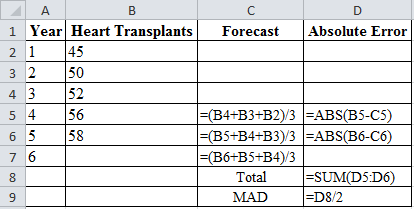
Calculation of the forecast for year 4:

$\begin{array}{c}\text{Moving}\text{average}=\frac{45+50+52}{3}\\ =49\end{array}$

To calculate the forecast for year 4, divide the summation of the values from years 1, 2 and 3 and divide by 3. The corresponding value 49 is the forecast for year 4. The 3-year moving average for year 4 is 49.

Calculation of the forecast for year 5:

$\begin{array}{c}\text{Moving}\text{average}=\frac{50+52+56}{3}\\ =52.67\end{array}$

To calculate the forecast for year 5, divide the summation of the values from years 2, 3 and 4 and divide by 3. The corresponding value 52.67 is the forecast for year 5. The 3-year moving average for year 5 is 52.67.

Calculation of the forecast for year 6:

$\begin{array}{c}\text{Moving}\text{average}=\frac{52+56+58}{3}\\ =55.33\end{array}$

To calculate the forecast for year 6, divide the summation of the values from years 3, 4, 5 and divide by 3. The corresponding value 55.33 is the forecast for year 5. The 3-year moving average for year 5 is 55.33.

Calculation of MAD using 3-year moving average:

Formula to calculate the Mean Absolute Deviation:

$\text{MAD}=\frac{{\displaystyle \sum \left|\text{Actual}-\text{Forecast}\right|}}{n}$

Calculation of the absolute error for year 4:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|56-49\right|\\ =\left|7\right|\\ =7\end{array}$

The absolute error for year 4 is the modulus of the difference between 56 and 49, which corresponds to 7. Therefore, the absolute error for year 4 is 7.

Calculation of the absolute error for year 5:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|58-52.67\right|\\ =\left|5.33\right|\\ =5.33\end{array}$

The absolute error for year 4 is the modulus of the difference between 58 and 52.67, which corresponds to 5.33. Therefore, the absolute error for year 4 is 5.33.

Calculation of the Mean Absolute Deviation using 3-year moving average:

$\begin{array}{c}\text{MAD}=\frac{{\displaystyle \sum \left|\text{Actual}-\text{Forecast}\right|}}{n}\\ =\frac{7+5.33}{2}\\ =\frac{12.333}{2}\\ =6.1666\end{array}$ (3)

Upon the substitution of the summation value of the absolute error for 2 years, that is,12.333is divided by number of years. That is, 2 yields MAD of 6.1666.

Hence, the demand forecast for years 4, 5 and 6 is 49, 52.67 and 55.33.

Summary Introduction

To determine: Find the demand forecast in year 1 through 6using trend projection.

Answer to Problem 13P

The forecast in year 1 through 6using trend projection is62.1.

Explanation of Solution

Given information:

Year	1	2	3	4	5	6
Heart Transplants	45	50	52	56	58

Formula to calculate the demand forecast

$\widehat{\text{y}}=\text{a}+\text{bx}$

Where,

$\begin{array}{c}\widehat{\text{y}}=\text{computed value of the variable}\\ \text{a}=\text{y-axis intercept}\\ \text{b}=\text{slope of the regression line}\\ \text{x}=\text{the independent variable}\end{array}$

$\text{b}=\frac{\sum \text{xy}-n\overline{\text{x}}\overline{\text{y}}}{\sum {\text{x}}^{\text{2}}-\text{n}{\overline{\text{x}}}^{\text{2}}}$

Where,

$\begin{array}{l}\text{b}=\text{slope of the regression line}\\ \sum =\text{ summation sign}\\ \text{x}=\text{known values of the independent variables}\\ \text{y}=\text{known values of the dependent variables}\end{array}$

$\begin{array}{l}\overline{\text{x}}=\text{average of the x - values}\\ \overline{\text{y}}=\text{average of the y - values}\\ \text{n }=\text{ number of data points}\end{array}$

Year (x)	Heart Transplants (y)	xy	x^2
1	45	45	1
2	50	100	4
3	52	156	9
4	56	224	16
5	58	290	25
∑=15	∑=261	∑=815	∑=55

Excel worksheet

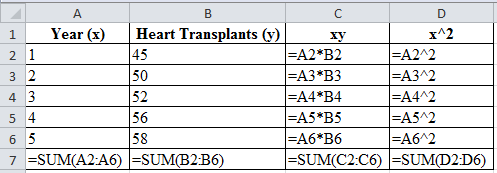
Substituting the values in the above formula

Calculation of average of x values $\overline{x}$:

$\begin{array}{c}\overline{\text{x}}=\frac{{\displaystyle \sum _{i=1}^5\text{x}}}{n}\\ =\frac{15}{5}\\ =\text{3}\end{array}$

The average of x values is obtained by dividing the summation of x values, that is, (1+2+…+5) with the number of period n. That is, 5. The value of $\overline{x}$= 3.

Calculation of average of y values $\overline{y}$:

$\begin{array}{c}\overline{\text{y}}=\frac{{\displaystyle \sum _{i=1}^{5}y}}{n}\\ =\frac{\text{261}}{5}\\ =52.2\end{array}$

The average of y values is obtained by dividing the summation of sales with the number of period n. That is, 5. The value of $\overline{y}$= 52.2.

Calculation of slope of regression line‘b’:

$\begin{array}{c}\text{b}=\frac{\sum \text{xy}-n\overline{\text{x}}\overline{\text{y}}}{\sum {\text{x}}^{\text{2}}-n{\overline{\text{x}}}^{\text{2}}}\\ =\frac{815-\left(5\times 3\times 52.2\right)}{55-\left(5\times 3^2\right)}\\ =\frac{32}{10}\\ =3.2\end{array}$

The summation of product of sales (y) with x values is ∑xy = 815, the product of number of years (n), the average of x values and the average of y values is obtained. That is, $n\overline{\text{x}}\overline{\text{y}}$=783. The difference between 815and 783 is 32.

The summation of square of x values, that is, 55 is subtracted from the product of the number of years. That is,5 with average of x values;3. The resultant value is 10. The slope of regression line is obtained by dividing 32 with 10. The value of ‘b’ is 3.2.

Calculation of y-axis intercept ‘a’:

$\begin{array}{c}\text{a}=\overline{\text{y}}-\text{b}\overline{\text{x}}\\ =\text{52}\text{.5}-\left(\text{3}\text{.2}\times \text{3}\right)\\ =\text{42}\text{.9}\end{array}$

The y-axis intercept is obtained by the difference between average of y values and values obtained by the product of slope of regression line with average of x values. The resultant value of ‘a’ is 42.9.

Calculation of the forecast for years 1 through 6:

a=	42.9	b=		3.2
Year (x)	Heart Transplants (y)	xy	x^2	Forecast
1	45	45	1	46.1
2	50	100	4	49.3
3	52	156	9	52.5
4	56	224	16	55.7
5	58	290	25	58.9
6				62.1

Excel worksheet:

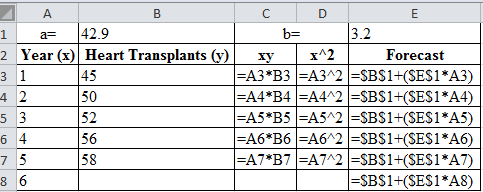
Calculation of forecast of year 1:

$\begin{array}{c}\widehat{\text{y}}=\text{a}+\text{bx}\\ =\text{42}\text{.9}+\left(\text{3}\text{.2}\times 1\right)\\ =\text{46}\text{.1}\end{array}$

The forecast for year 1 is obtained by the summation of the product of slope of regression line and forecasted year, with the y-axis intercept. The forecasted value obtained is 46.1.

Calculation of forecast of year 2:

$\begin{array}{c}\widehat{\text{y}}=\text{a}+\text{bx}\\ =\text{42}\text{.9}+\left(\text{3}\text{.2}\times 2\right)\\ =\text{49}\text{.3}\end{array}$

The forecast for year 2 is obtained by the summation of the product of slope of regression line and forecasted year, with the y-axis intercept. The forecasted value obtained is 49.3.

Calculation of forecast of year 3:

$\begin{array}{c}\widehat{\text{y}}=\text{a}+\text{bx}\\ =\text{42}\text{.9}+\left(\text{3}\text{.2}\times 3\right)\\ =\text{52}\text{.5}\end{array}$

The forecast for year 3 is obtained by the summation of the product of slope of regression line and forecasted year, with the y-axis intercept. The forecasted value obtained is 52.5.

Calculation of forecast of year 4:

$\begin{array}{c}\widehat{\text{y}}=\text{a}+\text{bx}\\ =\text{42}\text{.9}+\left(\text{3}\text{.2}\times 4\right)\\ =\text{55}\text{.7}\end{array}$

The forecast for year 4 is obtained by the summation of the product of slope of regression line and forecasted year, with the y-axis intercept. The forecasted value obtained is 55.7.

Calculation of forecast of year 5:

$\begin{array}{c}\widehat{\text{y}}=\text{a}+\text{bx}\\ =\text{42}\text{.9}+\left(\text{3}\text{.2}\times 5\right)\\ =\text{58}\text{.9}\end{array}$

The forecast for year 5 is obtained by the summation of the product of slope of regression line and forecasted year, with the y-axis intercept. The forecasted value obtained is 58.9.

Calculation of forecast of year 6:

$\begin{array}{c}\widehat{\text{y}}=\text{a}+\text{bx}\\ =\text{42}\text{.9}+\left(\text{3}\text{.2}\times 6\right)\\ =\text{62}\text{.1}\end{array}$

The forecast for year 6 is obtained by the summation of the product of slope of regression line and forecasted year, with the y-axis intercept. The forecasted value obtained is 62.1.

Formula to calculate the Mean Absolute Deviation:

$\text{MAD}=\frac{{\displaystyle \sum \left|\text{Actual}-\text{Forecast}\right|}}{n}$

Calculation of MAD using trend projection:

a=	42.9	b=		3.2
Year (x)	Heart Transplants (y)	xy	x^2	Forecast	Absolute error
1	45	45	1	46.1	1.1
2	50	100	4	49.3	0.7
3	52	156	9	52.5	0.5
4	56	224	16	55.7	0.3
5	58	290	25	58.9	0.9
6				62.1
				Total	3.5
				MAD	0.7

Excel worksheet:

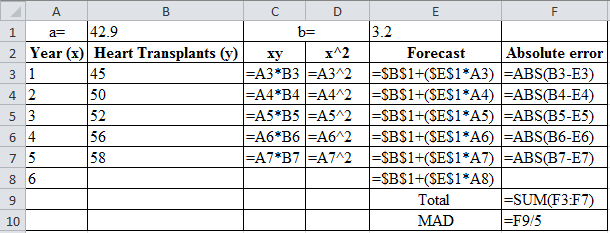
Calculation of the absolute error for year 1:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|45-46.1\right|\\ =\left|-1.1\right|\\ =1.1\end{array}$

The absolute error for year 1 is the modulus of the difference between 45 and 46.1, which corresponds to 1.1. Therefore, the absolute error for year 1 is 1.1.

Calculation of the absolute error for year 2:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|50-49.3\right|\\ =\left|0.7\right|\\ =0.7\end{array}$

The absolute error for year 2 is the modulus of the difference between 50 and 49.3, which corresponds to 0.7. Therefore, the absolute error for year 2 is 0.7.

Calculation of the absolute error for year 3:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|52-52.5\right|\\ =\left|-0.5\right|\\ =0.5\end{array}$

The absolute error for year 3 is the modulus of the difference between 52 and 52.5, which corresponds to 0.5. Therefore, the absolute error for year 3 is 0.5.

Calculation of the absolute error for year 4:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|56-55.7\right|\\ =\left|0.3\right|\\ =0.3\end{array}$

The absolute error for year 4 is the modulus of the difference between 56 and 55.7, which corresponds to 0.3. Therefore, the absolute error for year 4 is 0.3.

Calculation of the absolute error for year 5:

$\begin{array}{c}\text{Absolute}\text{error}=\left|\text{Actual}-\text{Forecast}\right|\\ =\left|58-58.9\right|\\ =\left|-0.9\right|\\ =0.9\end{array}$

The absolute error for year 5 is the modulus of the difference between 58 and 58.9, which corresponds to 0.9. Therefore, the absolute error for year 5 is 0.9.

Calculation of the Mean Absolute Deviation using trend projection:

$\begin{array}{c}\text{MAD}=\frac{{\displaystyle \sum \left|\text{Actual}-\text{Forecast}\right|}}{n}\\ =\frac{1.1+0.7+0.5+0.3+0.9}{5}\\ =\frac{3.5}{5}\\ =0.7\end{array}$ (4)

Upon the substitution of summation value of absolute error for 5 years, that is,3.5is divided by the number of years. That is,5 yields MAD of 0.7.

Thus, the forecast in year 1 through 6 using trend projection is 62.1.

Summary Introduction

To determine: Compare the MAD of exponential smoothing, 3-year moving average and trend projection and infer the best method.

Explanation of Solution

On Comparing MAD from the four methods, (refer to equations (1), (2), (3) and (4)) it can be inferred that trend projection is the best methods since it has the least MAD.