Chapter 4, Problem 4.6HP

In the circuit shown in Figure P4.4, assume $R=2\Omega$ and $L=4H$ . Also, let:
$i\left(t\right)=\{\begin{array}{cc}0& -\infty <t<0\\ 2t& 0\le t<5s\\ 10-4t& 5\le t<12s\\ 2& 12s\le t<\infty \end{array}$

Find:
a. The energy stored in the inductor for all time.
b. The energy delivered by the source for all time.

To determine

(a)

The energy stored in the inductor.

Answer to Problem 4.6HP

The energy stored in the inductor for different time interval is $w_L=\{\begin{array}{l}0-\infty <t<0\\ 8t^{2}0\le t<5\text{s}\\ 32t^2-160+2005\le t<12\\ 812\le t<\infty \end{array}$ .

Explanation of Solution

Calculation:

The given diagram is shown in Figure 1

  

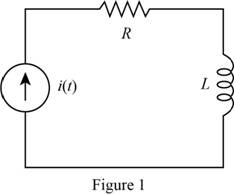
The expression for the energy stored in the conductor is given by,

  $w_L\left(t\right)=\frac{1}{2}L{\left[i\left(t\right)\right]}^2$....... (1)

Substitute $0$ for $i\left(t\right)$ and $4\text{H}$ for $L$ in the above equation.

  $\begin{array}{c}{w}_L\left(t\right)=\frac{1}{2}\left(4\text{H}\right){\left[\left(0\right)\right]}^2\\ =0\text{J}\end{array}$

Substitute $2t$ for $i\left(t\right)$ and $4\text{H}$ for $L$ in equation (1).

  $\begin{array}{c}{w}_L\left(t\right)=\frac{1}{2}\left(4\text{H}\right){\left[\left(2t\right)\right]}^2\\ =8t^2\text{J}\end{array}$

Substitute $10-4t$ for $i\left(t\right)$ and $4\text{H}$ for $L$ in equation (1).

  $\begin{array}{c}{w}_L\left(t\right)=\frac{1}{2}\left(4\text{H}\right){\left(10-4t\right)}^2\\ =2\left(16t^2-80t+100\right)\text{J}\\ =\text{32}{t}^2-160t+200\end{array}$

Substitute $2$ for $i\left(t\right)$ and $4\text{H}$ for $L$ in equation (1).

  $\begin{array}{c}{w}_L\left(t\right)=\frac{1}{2}\left(4\text{H}\right){\left(2\right)}^2\\ =8\text{J}\end{array}$

The expression for the energy stored in the inductor for different time interval is given by,

  $w_L=\{\begin{array}{l}0-\infty <t<0\\ 8t^{2}0\le t<5\text{s}\\ 32t^2-160+2005\le t<12\\ 812\le t<\infty \end{array}$

Conclusion:

Therefore, the energy stored in the inductor for different time interval is $w_L=\{\begin{array}{l}0-\infty <t<0\\ 8t^{2}0\le t<5\text{s}\\ 32t^2-160+2005\le t<12\\ 812\le t<\infty \end{array}$ .

To determine

(b)

Theenergy delivered by the source.

Answer to Problem 4.6HP

The energy delivered by the source for various time interval is $\{\begin{array}{l}0-\infty <t<0\\ 8t^2\left(1+\frac{t}{3}\right)0\le t<5\text{s}\\ \frac{32t^2}{3}-48t^2+40t+200\text{J}5\le t<12\\ 8t+922412\le t<\infty \end{array}$ .

Explanation of Solution

Calculation:

The expression for the energy stored in the conductor is given by,

  $w\left(t\right)=\frac{1}{2}L{\left[i\left(t\right)\right]}^2+{\displaystyle {\int }_{t_1}^{t_2}{i}^{2}Rdt}$ ....... (2)

Substitute, $-\infty$ for $t_1$, $0$ for $t_2$, $0$ for $i\left(t\right)$, $2\Omega$ for $R$ and $4\text{H}$ for $L$ in the above equation.

  $\begin{array}{c}w\left(t\right)=\frac{1}{2}\left(4\text{H}\right){\left[\left(0\right)\right]}^2+{\displaystyle {\int }_{-\infty }^0{\left(0\right)}^2\left(2\Omega \right)dt}\\ =0\text{J}\end{array}$

Substitute, $0$ for $t_1$, $5$ for $t_2$, $2t$ for $i\left(t\right)$, $2\Omega$ for $R$ and $4\text{H}$ for $L$ in equation (2)

  $\begin{array}{c}w\left(t\right)=\frac{1}{2}\left(4\text{H}\right){\left[\left(2t\right)\right]}^2+{\displaystyle {\int }_0^{10}{\left(2t\right)}^2\left(2\Omega \right)dt}\\ =8t^2\text{J+}{\left[\frac{t^3}{3}\right]}_0^5\\ =\left(8t^2+\frac{{\left(5\right)}^3}{3}\right)\text{J}\\ =8t^2+333.33\text{J}\end{array}$

The energy dissipated by the resistor from $5\le t<12\text{s}$ is calculated as,

  $w_R\left(t\right)={\displaystyle {\int }_0^t{i}^2\left(t\right)Rdt}$

Substitute $\left(10-4t\right)$ for $i\left(t\right)$ and $2\Omega$ for $R$ in the above equation.

  $\begin{array}{c}{w}_R\left(t\right)={\displaystyle {\int }_5^t{\left(10-4t\right)}^2\left(2\text{H}\right)dt}+333.3J\\ =\left[{2\left(100t-\frac{80t^2}{2}+\frac{16t^3}{3}\right)|}_5^t\right]+333.3\text{J}\\ \text{=}\left(200t-80t^2+\frac{32t^3}{3}-1000+2000-\frac{4000}{3}\right)+333.33\\ =200t-80t^2+\frac{32t^3}{3}+0\end{array}$

Solve further as,

  $w_R\left(t\right)=200t-80t^2+\frac{32t^3}{3}\text{J}$

Substitute $12\text{s}$ for $t$ in the above equation.

  $\begin{array}{c}{w}_R\left(t\right)=200\left(12\text{s}\right)-80{\left(12\text{s}\right)}^2+\frac{32{\left(12\text{s}\right)}^3}{3}\text{J}\\ =\text{2400}-\text{80}\left(144\right)+32\left(576\right)\\ =9312\end{array}$

The expression for the power delivered by the source for $5\le t<12\text{s}$ is given by,

  $w_T\left(t\right)=w_L\left(t\right)+w_R\left(t\right)$

Substitute $\frac{32t^2}{3}-48t^2+40t+200\text{J}$ for $w_R\left(t\right)$ and $\text{32}{t}^2-160t+200$ for $w_L\left(t\right)$ in the above equation.

  $\begin{array}{c}{w}_T\left(t\right)=32t^2-160t+200+200t-80t^2+\frac{32t^2}{3}\\ =\frac{32t^2}{3}-48t^2+40t+200\text{J}\end{array}$

The expression for the energy dissipated in the resistor from $12\le t<\infty$ is given by,

  $w_R\left(t\right)={\displaystyle {\int }_{12}^t{i}^2\left(t\right)Rdt}+9312\text{J}$

Substitute $2$ for $i\left(t\right)$ and $2\Omega$ for $R$ in the above equation.

  $\begin{array}{c}{w}_R\left(t\right)={\displaystyle {\int }_{12}^t{\left(2\right)}^2\left(2\Omega \right)dt}+9312\text{J}\\ =8\left(t-12\right)+9312\text{J}\\ =\text{8}t+9216\text{J}\end{array}$

The expression for the energy delivered by the source for the time $12\text{s}\le t<\infty$ is given by,

  $w_T\left(t\right)=w_L\left(t\right)+w_R\left(t\right)$

Substitute $\text{8}t+9216\text{J}$ for $w_R\left(t\right)$ and $8\text{J}$ for $w_L\left(t\right)$ in the above equation.

  $\begin{array}{c}{w}_T\left(t\right)=w_L\left(t\right)+w_R\left(t\right)\\ =8+8\left(t\right)+9216\\ =8t+9224\text{J}\end{array}$

The energy delivered by the source for various time interval is given by,

  $w_T=\{\begin{array}{l}0-\infty <t<0\\ 8t^2\left(1+\frac{t}{3}\right)0\le t<5\text{s}\\ \frac{32t^2}{3}-48t^2+40t+200\text{J}5\le t<12\\ 8t+922412\le t<\infty \end{array}$

Conclusion:

Therefore, the energy delivered by the source for various time interval is $\{\begin{array}{l}0-\infty <t<0\\ 8t^2\left(1+\frac{t}{3}\right)0\le t<5\text{s}\\ \frac{32t^2}{3}-48t^2+40t+200\text{J}5\le t<12\\ 8t+922412\le t<\infty \end{array}$ .