Chapter 4, Problem 4.10HP

To determine

The current $i_L\left(t\right)$ through the inductor.

Answer to Problem 4.10HP

The expression for the current through the inductor for different time interval is $i_L\left(t\right)=\{\begin{array}{l}3000t-{10}^5{t}^2+\text{2}\text{.55}\text{A}\text{for}0<t<5\text{ms}\\ \left(50\text{H}\right)20t+i_L\left(10\text{ms}\right)\text{for}\text{5}<t<10\text{ms}\\ 100t+22.55\text{A}\text{for}t>10\text{ms}\end{array}$ .

Explanation of Solution

Calculation:

The given diagram is shown in Figure 1

  

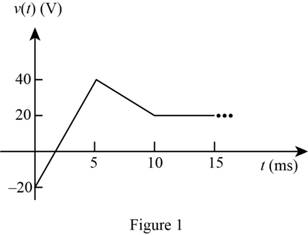
The conversion from $\text{ms}$ to $\text{s}$ is given by,

  $1\text{ms}={10}^{-3}\text{s}$

The conversion from $\text{20}\text{ms}$ to $\text{s}$ is given by,

  $\text{20}\text{ms}=20\times {10}^{-3}\text{s}$

The conversion from $\text{5}\text{ms}$ to $\text{s}$ is given by,

  $\text{5}\text{ms}=5\times {10}^{-3}\text{s}$

The conversion from $\text{10}\text{ms}$ to $\text{s}$ is given by,

  $\text{10}\text{ms}=5\times {10}^{-3}\text{s}$

The conversion from $\text{mH}$ into $\text{H}$ is given by,

  $1\text{mH}={\text{10}}^{-3}\text{H}$

The conversion from $\text{20}\text{mH}$ into $\text{H}$ is given by,

  $\text{20}\text{mH}=20\times {\text{10}}^{-3}\text{H}$

The conversion from $\text{mA}$ into $\text{A}$ is given by,

  $1\text{mA}={\text{10}}^{-3}\text{A}$

The conversion from $\text{50}\text{mA}$ into $\text{A}$ is given by,

  $\text{50}\text{mA}=50\times {\text{10}}^{-3}\text{A}$

From the graph the expression for the voltage between the points $\left(0,-20\text{ms}\right)$ and $\left(5\text{ms},40\text{V}\right)$ is calculated as,

  $\begin{array}{c}v\left(t\right)=\frac{40+20}{5\times {10}^{-3}-0}\left(t-0\right)-20\\ =12000t-20\text{V}\end{array}$

From the graph the expression for the voltage between the points $\left(5\text{ms},40\text{V}\right)$ and $\left(10\text{ms},20\text{V}\right)$ is calculated as,

  $\begin{array}{c}v\left(t\right)=\left(\frac{20-40}{10\times {10}^{-3}-5\times {10}^{-3}}\right)\left(t-5\times {10}^{-3}\right)+40\\ =-4000t+20+40\\ =-4000t+60\text{V}\end{array}$

From the graph the expression for the voltage at $t>10\text{ms}$ is given by,

  $v\left(t\right)=20\text{V}$

The expression for the voltage across the inductor is given by,

  $v\left(t\right)=\{\begin{array}{l}12000t-20\text{V}\text{for}0<t<5\text{ms}\\ -4000t+60\text{V}\text{for}\text{5}<t<10\text{ms}\\ 20\text{V}\text{for}t>10\text{ms}\end{array}$

The expression for the current through the inductor is given by,

  $i_L\left(t\right)=\frac{1}{L}{\displaystyle \int v\left(t\right)dt}$ ..........(1)

Substitute $20\times {\text{10}}^{-3}\text{H}$ for $L$ and $12000t-20\text{V}$ for $v\left(t\right)$ in the above equation.

  $\begin{array}{c}{i}_L\left(t\right)=\frac{1}{20\times {\text{10}}^{-3}\text{H}}{\displaystyle \int \left(12000t-20\text{V}\right)dt}\\ =\left(50\text{H}\right)\left[\frac{12000t^2}{2}-20t\right]+i_L\left(0\right)\\ =\left(3\times {10}^5\right)t^2-1000t+i_L\left(0\right)\end{array}$

Substitute $50\times {\text{10}}^{-3}\text{A}$ for $i_L\left(0\right)$ in the above equation.

  $i_L\left(t\right)=\left(3\times {10}^5\right)t^2-1000t+50\times {\text{10}}^{-3}\text{A}$

Substitute $5\times {10}^{-3}\text{s}$ for $t$ in the above equation.

  $\begin{array}{c}{i}_L\left(5\times {10}^{-3}\text{s}\right)=\left(3\times {10}^5\right){\left(5\times {10}^{-3}\text{s}\right)}^2-1000\left(5\times {10}^{-3}\text{s}\right)+50\times {\text{10}}^{-3}\text{A}\\ =\left(\text{7}\text{.5}-5+0.05\right)\text{A}\\ =\text{2}\text{.55}\text{A}\end{array}$

Substitute $20\times {\text{10}}^{-3}\text{H}$ for $L$ and $-4000t+60\text{V}$ for $v\left(t\right)$ equation (1)

  $\begin{array}{c}{i}_L\left(t\right)=\frac{1}{20\times {\text{10}}^{-3}\text{H}}{\displaystyle \int \left(-4000t+60\text{V}\right)dt}\\ =\left(50\text{H}\right)\left[60t-\frac{4000t^2}{2}\right]+i_L\left(\text{5}\text{ms}\right)\end{array}$

Substitute $\text{2}\text{.55}\text{A}$ for $i_L\left(\text{5}\text{ms}\right)$ in the above equation.

  $\begin{array}{c}{i}_L\left(t\right)=\left(50\text{H}\right)\left[60t-\frac{4000t^2}{2}\right]+\text{2}\text{.55}\text{A}\\ =3000t-{10}^5{t}^2+\text{2}\text{.55}\text{A}\end{array}$

Substitute $10\text{ms}$ for $t$ in the above equation.

  $\begin{array}{c}{i}_L\left(t\right)=3000\left(10\times {10}^{-3}\text{s}\right)-{10}^5{\left(10\times {10}^{-3}\text{s}\right)}^2+\text{2}\text{.55}\text{A}\\ =30-10+2.55\\ =22.55\text{A}\end{array}$

Substitute $20\times {\text{10}}^{-3}\text{H}$ for $L$ and $20\text{V}$ for $v\left(t\right)$ equation (1)

  $\begin{array}{c}{i}_L\left(t\right)=\frac{1}{20\times {\text{10}}^{-3}\text{H}}{\displaystyle \int \left(20\text{V}\right)dt}\\ =\left(50\text{H}\right)20t+i_L\left(10\text{ms}\right)\end{array}$

Substitute $22.55\text{A}$ for $i_L\left(10\text{ms}\right)$ in the above equation.

  $\begin{array}{c}{i}_L\left(t\right)=\left(50\text{H}\right)20t+22.55\text{A}\\ =100t+22.55\text{A}\end{array}$

The expression for the current through the inductor is given by, $i_L\left(t\right)=\{\begin{array}{l}3000t-{10}^5{t}^2+\text{2}\text{.55}\text{A}\text{for}0<t<5\text{ms}\\ \left(50\text{H}\right)20t+i_L\left(10\text{ms}\right)\text{for}\text{5}<t<10\text{ms}\\ 100t+22.55\text{A}\text{for}t>10\text{ms}\end{array}$

Conclusion:

Therefore, the expression for the current through the inductor for different time interval is $i_L\left(t\right)=\{\begin{array}{l}3000t-{10}^5{t}^2+\text{2}\text{.55}\text{A}\text{for}0<t<5\text{ms}\\ \left(50\text{H}\right)20t+i_L\left(10\text{ms}\right)\text{for}\text{5}<t<10\text{ms}\\ 100t+22.55\text{A}\text{for}t>10\text{ms}\end{array}$ .