Chapter 4, Problem 4.35P

To determine

Calculate the gas pressure inside the platinum capsule after $100$ years which contains $100$ mg of radium as $RaB{r}_2$ . Originally capsule contains air at atmospheric pressure at the room.

Answer to Problem 4.35P

Gas pressure is $23.3$ atmosphere inside the capsule due to helium gas formed by the decay of radium.

Explanation of Solution

When Radium-226 decay, it emits a particles each a particle is a helium nucleus with 2 electrons and forms helium gas which produces pressure in a capsule.

226 Ra emits 4 alpha particles per decay immediately after secular equilibrium and there is the formation of the fifth a particle.

  $\begin{array}{l}226Raemits1\alpha \hfill \\ 222Rnemits1\alpha \hfill \\ 218Poemits1\alpha \hfill \\ 214Poemits1\alpha \hfill \\ 210Poemits1\alpha \hfill \end{array}$

The fraction of $\alpha$ is specified by comparing the area under the curve to the total area

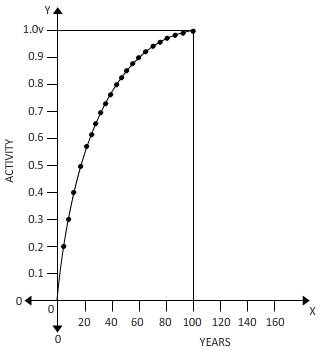
Above carve shows a fraction of a to helium over 100 years.

Fraction=Area under curve/Total area

= $\frac{{{\displaystyle \int }}_0^{100}\text{Ae}\left(1-{\text{e}}^{-\text{λt}}\right)\text{it}}{\text{Ae}}\times \text{T}$

Integrating from $T=0toT=100$

  $Fraction=A_E\underset{0}{\overset{T}{{\displaystyle \int }}}dt-\underset{0}{\overset{T}{{\displaystyle \int }}}\frac{e^{-\lambda tdt}}{A_E}\times T$

  $=T-[1/\lambda [1-e^{-}{}^{\lambda t}]]/T$

  $=100-[1/0.0359(1-e^{-}0.0359\times 100)]/100$

Fraction= $0.73\text{ for }1\alpha$ particle

Four alpha particles emitted over $100$ years are

  $\begin{array}{l}=4+0.73\hfill \\ =4.73\alpha paticles.\hfill \end{array}$

We know that,

  $A=A_0{e}^{-\lambda t}$ ------------------(1)

To calculate the fraction of decay

  $A_{decay}=A_0\left(1-e^{-\lambda t}\right)$ -------------------(2)

Rearranging, (1) and (2)

  $A_{decay}/A=1-e^{-\lambda t}$

  $\begin{array}{l}ForT1/2=1620yrs\\ \lambda =0.693/1620\\ =0.000428y{r}^{-}{}^1\\ and\\ T=100\\ A\text{decay}/A\\ =1-e^{-0.000428\times 100}=0.042\end{array}$

Hence $0.042\text{ is a fraction of}{}^{226}Ra$ which decays over $100$ years.

  $100{\text{ mg of }}^{{}_{226}}\text{Ra}$ is contained in a capsule after $100$ years.

  $100\times 0.042=4.2$ mg of radium in decaying over $100$ years.

To calculate helium atoms formed over $100$ years,

  $\begin{array}{l}=4.2mg\times 19/1000mg\times 1mol226Ra/226g\times 6.02\times {10}^{23}\times 4.73\lambda /atomdecay\\ =5.3\times {10}^{19}atomsofhelium\\ =5.3\times {10}^{19}/6.02\times {10}^{23}\\ =8.8\times {10}^{-}{}^{5}molesofhelium\end{array}$ 4

We have,

The dimension of the capsule,

  $\begin{array}{l}L=4cmR\\ =1mm\\ =0.1cm\\ V=\pi r^2\times L\\ =\pi \times {0.1}^2\times 4\\ =0.126{\text{cm}}^{\text{3}}\\ =1.26\times {10}^{-}{}^{4}L\end{array}$

The molecular weight of RaBr₂,

  $226+\left(2\times 79.916\right)=385.83gm/mole$

The volume of RaBr₂ is,

  $(385-83/226)\times 0.1/5.79\times 1000=2.95\times {10}^{-}{}^5$

Volume available for gas=volume of capsule-volume of RaBr₂

  $\begin{array}{l}=(1.26\times {10}^{-}{}^4)-(2.95\times {10}^{-}{}^5)\\ =9.65\times {10}^{-}{}^{5}L\end{array}$

According to Ideal gas low

  $\begin{array}{l}T=250C=2980K\\ v=9.65\times {10}^{-}{}^{5}L\\ n=8.8\times {10}^{-}{}^{5}mole\\ R=0.082\\ PV=nRT\\ P=nRT/V\\ =8.8\times {10}^{-}{}^5\times 0.082\times 298/9.65\times {10}^{-}{}^{5}L\\ =22.3\text{atm}\text{.}\end{array}$

The pressure of helium formed by the decay of radium is 22.3 atmospheres. But originally capsule contains an air of 1 atmospheric pressure. Hence this initial pressure must be considered.

Thus, pressure= $22.3+1=23.3atm.$

Conclusion:

We can conclude about this problem that, when Radium-226 decays. It emits a particles having helium nucleus with two electrons and produces helium gas. Ideal gas law is used to calculate the pressure of helium gas. The gas pressure inside the capsule is 23.3 atm due to the formation of helium gas by the decay of radium.