Chapter 4, Problem 101P

Combine your results from Prob. 4—100 to form the two-dimensional strain rate tensor in the xy-plane, ${\epsilon }_{ij}=\left({}_{{\epsilon }_{yx}{\epsilon }_{yy}}^{{\epsilon }_{xx}{\epsilon }_{xy}}\right)$ Are the x- and y-axes principal axes?

To determine

The two-dimensional strain rate tensor ${\epsilon }_{ij}$in the $xy$-plane.

Answer to Problem 101P

The two-dimensional strain rate tensor ${\epsilon }_{ij}$in the $xy$-plane is:

  ${\epsilon }_{ij}=\left(\begin{array}{cc}0& \frac{1}{4\mu }\times \frac{dP}{dx}(2y-h)\\ \frac{1}{4\mu }\times \frac{dP}{dx}(2y-h)& 0\end{array}\right)$

Explanation of Solution

The given figure represents Poiseuille flow between two plates.

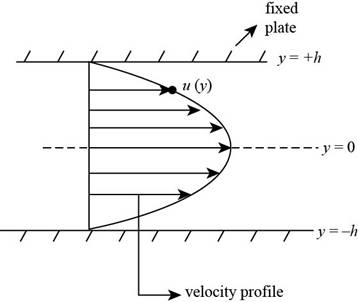
Figure-(1)

Write the expression for two-dimensional strain rate tensor along $xy$plane.

${\epsilon }_{ij}=\left(\begin{array}{cc}{\epsilon }_{xx}& {\epsilon }_{xy}\\ {\epsilon }_{yx}& {\epsilon }_{yy}\end{array}\right)$...... (I)

Here, the strain rate tensor is ${\epsilon }_{ij}$, strain rate in $x$direction is ${\epsilon }_{xx}$, strain rate along the $y$direction is ${\epsilon }_{yy}$shear strain rate in $xy$plane is ${\epsilon }_{xy}$and shear strain rate in $yx$direction is ${\epsilon }_{yx}$.

Write the expression for the velocity component along $x$direction.

$u=\frac{1}{2\mu }\times \frac{dP}{dx}(y^2-hy)$...... (II)

Here, the velocity along $x$direction is $u$, viscosity of the fluid is $\mu$, the pressure gradient is $\frac{dP}{dx}$, distance between the two plates is $h$.

Write the expression for the velocity component is $y$direction.

$v=0$...... (III)

Write the expression for linear strain rate along the $x$direction.

${\epsilon }_{xx}=\frac{du}{dx}$...... (IV)

Substitute $u=\frac{1}{2\mu }\times \frac{dP}{dx}(y^2-hy)$for u in Equation (IV).

$\begin{array}{c}{\epsilon }_{xx}=\frac{d\left(\frac{1}{2\mu }\times \frac{dP}{dx}(y^2-hy)\right)}{dx}\\ =\frac{d\left(\frac{1}{2\mu }\times \frac{dP}{dx}\left(y^2\right)\right)}{dx}-\frac{d\left(\frac{1}{2\mu }\times \frac{dP}{dx}\left(hy\right)\right)}{dx}\\ =0-0\\ =0\end{array}$

Write the expression for linear strain rate along the $y$direction.

${\epsilon }_{yy}=\frac{dv}{dy}$...... (V)

Substitute 0 for v in the Equation (V).

$\begin{array}{c}{\epsilon }_{yy}=\frac{dv}{dy}\\ =\frac{d\left(0\right)}{dy}\\ =0\end{array}$

Write the expression for shear strain rate in $xy$plane.

${\epsilon }_{xy}=\frac{1}{2}\left(\frac{du}{dy}+\frac{dv}{dx}\right)$...... (VI)

Write the expression for shear strain rate in $yx$plane.

${\epsilon }_{yx}=\frac{1}{2}\left(\frac{dv}{dx}+\frac{du}{dy}\right)$

...... (VII)

Differentiate Equation (II) with respect to $y$.

$\begin{array}{c}\frac{du}{dy}=\frac{d\left(\frac{1}{2\mu }\times \frac{dP}{dx}(y^2-hy)\right)}{dy}\\ =\frac{1}{2\mu }\times \frac{dP}{dx}\left(\frac{d\left(y^2-hy\right)}{dy}\right)\\ =\frac{1}{2\mu }\times \frac{dP}{dx}(2y-h)\end{array}$

Differentiate Equation (III) with respect to $x$.

$\begin{array}{l}\frac{dv}{dx}=\frac{d\left(0\right)}{dx}\\ \frac{dv}{dx}=0\end{array}$

Calculation:

Substitute $\frac{1}{2\mu }\times \frac{dP}{dx}(2y-h)$for $\frac{du}{dy}$and $0$for $\frac{dv}{dx}$in Equation (VI).

$\begin{array}{c}{\epsilon }_{xy}=\frac{1}{2}\left(\frac{1}{2\mu }\times \frac{dP}{dx}(2y-h)+0\right)\\ =\frac{1}{2}\left(\frac{1}{2\mu }\times \frac{dP}{dx}(2y-h)\right)\\ =\left(\frac{1}{4\mu }\times \frac{dP}{dx}(2y-h)\right)\end{array}$

Substitute $\frac{1}{2\mu }\times \frac{dP}{dx}(2y-h)$for $\frac{du}{dy}$and $0$for $\frac{dv}{dx}$in Equation (VII).

$\begin{array}{c}{\epsilon }_{yx}=\frac{1}{2}\left(0+\frac{1}{2\mu }\times \frac{dP}{dx}(2y-h)\right)\\ =\frac{1}{2}\left(\frac{1}{2\mu }\times \frac{dP}{dx}(2y-h)\right)\\ =\left(\frac{1}{4\mu }\times \frac{dP}{dx}(2y-h)\right)\end{array}$

Substitute $\left(\frac{1}{4\mu }\times \frac{dP}{dx}(2y-h)\right)$for ${\epsilon }_{xy}$and $\left(\frac{1}{4\mu }\times \frac{dP}{dx}(2y-h)\right)$for ${\epsilon }_{yx}$in Equation (I).

${\epsilon }_{ij}=\left(\begin{array}{cc}0& \left(\frac{1}{4\mu }\times \frac{dP}{dx}(2y-h)\right)\\ \left(\frac{1}{4\mu }\times \frac{dP}{dx}(2y-h)\right)& 0\end{array}\right)$

Therefore, the two-dimensional strain rate tensor ${\epsilon }_{ij}$in the $xy$-plane is:

  ${\epsilon }_{ij}=\left(\begin{array}{cc}0& \frac{1}{4\mu }\times \frac{dP}{dx}(2y-h)\\ \frac{1}{4\mu }\times \frac{dP}{dx}(2y-h)& 0\end{array}\right)$

Conclusion:

The two-dimensional strain rate tensor ${\epsilon }_{ij}$in the $xy$-plane is

  ${\epsilon }_{ij}=\left(\begin{array}{cc}0& \frac{1}{4\mu }\times \frac{dP}{dx}(2y-h)\\ \frac{1}{4\mu }\times \frac{dP}{dx}(2y-h)& 0\end{array}\right)$