EBK PRECALCULUS W/LIMITS
4th Edition
ISBN: 9781337516853
Author: Larson
Publisher: CENGAGE CO
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 3.5, Problem 66E
a.
To determine
To identify the given model as exponential growth, exponential decay, gaussian, linear, logarithmic, logistic growth, quadratic or none of above.
a.
Expert Solution
Explanation of Solution
Let us consider the following graph
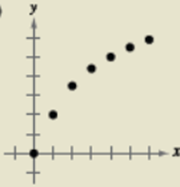
This is a logarithmic model since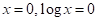
b.
To determine
To identify the given model as exponential growth, exponential decay, gaussian, linear, logarithmic, logistic growth, quadratic or none of above.
b.
Expert Solution
Explanation of Solution
Let us consider the following graph
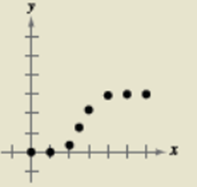
This is a logistic growth model since, it becomes constant after a while.
c.
To determine
To identify the given model as exponential growth, exponential decay, gaussian, linear, logarithmic, logistic growth, quadratic or none of above.
c.
Expert Solution
Explanation of Solution
Let us consider the following graph
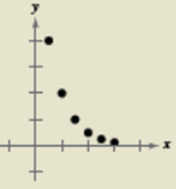
This is an exponential decay model.
d.
To determine
To identify the given model as exponential growth, exponential decay, gaussian, linear, logarithmic, logistic growth, quadratic or none of above.
d.
Expert Solution
Explanation of Solution
Let us consider the following graph
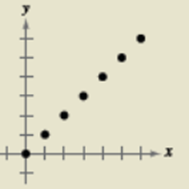
This graph is a linear model.
e.
To determine
To identify the given model as exponential growth, exponential decay, gaussian, linear, logarithmic, logistic growth, quadratic or none of above.
e.
Expert Solution
Explanation of Solution
Let us consider the following graph
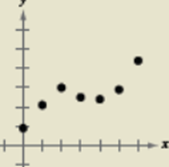
This graph doesn’t represent anything out of the given names.
f.
To determine
To identify the given model as exponential growth, exponential decay, gaussian, linear, logarithmic, logistic growth, quadratic or none of above.
f.
Expert Solution
Explanation of Solution
Let us consider the following graph
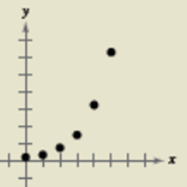
This graph is an exponential model.
g.
To determine
To identify the given model as exponential growth, exponential decay, gaussian, linear, logarithmic, logistic growth, quadratic or none of above.
g.
Expert Solution
Explanation of Solution
Let us consider the following graph
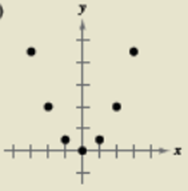
This is a quadratic model, as the value of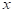 
is positive or negative, the graph will take the values in positive or negative quadrant for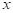 
h.
To determine
To identify the given model as exponential growth, exponential decay, gaussian, linear, logarithmic, logistic growth, quadratic or none of above.
h.
Expert Solution
Explanation of Solution
Let us consider the following graph
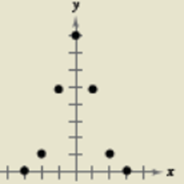
This is a Gaussian model.
Chapter 3 Solutions
EBK PRECALCULUS W/LIMITS
Ch. 3.1 - Prob. 1ECh. 3.1 - Prob. 2ECh. 3.1 - Prob. 3ECh. 3.1 - Prob. 4ECh. 3.1 - Prob. 5ECh. 3.1 - Prob. 6ECh. 3.1 - Prob. 7ECh. 3.1 - Prob. 8ECh. 3.1 - Prob. 9ECh. 3.1 - Prob. 10E
Ch. 3.1 - Prob. 11ECh. 3.1 - Prob. 12ECh. 3.1 - Prob. 13ECh. 3.1 - Prob. 14ECh. 3.1 - Prob. 15ECh. 3.1 - Prob. 16ECh. 3.1 - Prob. 17ECh. 3.1 - Prob. 18ECh. 3.1 - Prob. 19ECh. 3.1 - Prob. 20ECh. 3.1 - Prob. 21ECh. 3.1 - Prob. 22ECh. 3.1 - Prob. 23ECh. 3.1 - Prob. 24ECh. 3.1 - Prob. 25ECh. 3.1 - Prob. 26ECh. 3.1 - Prob. 27ECh. 3.1 - Prob. 28ECh. 3.1 - Prob. 29ECh. 3.1 - Prob. 30ECh. 3.1 - Prob. 31ECh. 3.1 - Prob. 32ECh. 3.1 - Prob. 33ECh. 3.1 - Prob. 34ECh. 3.1 - Prob. 35ECh. 3.1 - Prob. 36ECh. 3.1 - Prob. 37ECh. 3.1 - Prob. 38ECh. 3.1 - Prob. 39ECh. 3.1 - Prob. 40ECh. 3.1 - Prob. 41ECh. 3.1 - Prob. 42ECh. 3.1 - Prob. 43ECh. 3.1 - Prob. 44ECh. 3.1 - Prob. 45ECh. 3.1 - Prob. 46ECh. 3.1 - Prob. 47ECh. 3.1 - Prob. 48ECh. 3.1 - Prob. 49ECh. 3.1 - Prob. 50ECh. 3.1 - Prob. 51ECh. 3.1 - Prob. 52ECh. 3.1 - Prob. 53ECh. 3.1 - Prob. 54ECh. 3.1 - Prob. 55ECh. 3.1 - Prob. 56ECh. 3.1 - Prob. 57ECh. 3.1 - Prob. 58ECh. 3.1 - Prob. 59ECh. 3.1 - Prob. 60ECh. 3.1 - Prob. 61ECh. 3.1 - Prob. 62ECh. 3.1 - Prob. 63ECh. 3.1 - Prob. 64ECh. 3.1 - Prob. 65ECh. 3.1 - Prob. 66ECh. 3.1 - Prob. 67ECh. 3.1 - Prob. 68ECh. 3.1 - Prob. 69ECh. 3.1 - Prob. 70ECh. 3.1 - Prob. 71ECh. 3.1 - Prob. 72ECh. 3.1 - Prob. 73ECh. 3.1 - Prob. 74ECh. 3.1 - Prob. 75ECh. 3.1 - Prob. 76ECh. 3.1 - Prob. 77ECh. 3.1 - Prob. 78ECh. 3.1 - Prob. 79ECh. 3.1 - Prob. 80ECh. 3.2 - Prob. 1ECh. 3.2 - Prob. 2ECh. 3.2 - Prob. 3ECh. 3.2 - Prob. 4ECh. 3.2 - Prob. 5ECh. 3.2 - Prob. 6ECh. 3.2 - Prob. 7ECh. 3.2 - Prob. 8ECh. 3.2 - Prob. 9ECh. 3.2 - Prob. 10ECh. 3.2 - Prob. 11ECh. 3.2 - Prob. 12ECh. 3.2 - Prob. 13ECh. 3.2 - Prob. 14ECh. 3.2 - Prob. 15ECh. 3.2 - Prob. 16ECh. 3.2 - Prob. 17ECh. 3.2 - Prob. 18ECh. 3.2 - Prob. 19ECh. 3.2 - Prob. 20ECh. 3.2 - Prob. 21ECh. 3.2 - Prob. 22ECh. 3.2 - Prob. 23ECh. 3.2 - Prob. 24ECh. 3.2 - Prob. 25ECh. 3.2 - Prob. 26ECh. 3.2 - Prob. 27ECh. 3.2 - Prob. 28ECh. 3.2 - Prob. 29ECh. 3.2 - Prob. 30ECh. 3.2 - Prob. 31ECh. 3.2 - Prob. 32ECh. 3.2 - Prob. 33ECh. 3.2 - Prob. 34ECh. 3.2 - Prob. 35ECh. 3.2 - Prob. 36ECh. 3.2 - Prob. 37ECh. 3.2 - Prob. 38ECh. 3.2 - Prob. 39ECh. 3.2 - Prob. 40ECh. 3.2 - Prob. 41ECh. 3.2 - Prob. 42ECh. 3.2 - Prob. 43ECh. 3.2 - Prob. 44ECh. 3.2 - Prob. 45ECh. 3.2 - Prob. 46ECh. 3.2 - Prob. 47ECh. 3.2 - Prob. 48ECh. 3.2 - Prob. 49ECh. 3.2 - Prob. 50ECh. 3.2 - Prob. 51ECh. 3.2 - Prob. 52ECh. 3.2 - Prob. 53ECh. 3.2 - Prob. 54ECh. 3.2 - Prob. 55ECh. 3.2 - Prob. 56ECh. 3.2 - Prob. 57ECh. 3.2 - Prob. 58ECh. 3.2 - Prob. 59ECh. 3.2 - Prob. 60ECh. 3.2 - Prob. 61ECh. 3.2 - Prob. 62ECh. 3.2 - Prob. 63ECh. 3.2 - Prob. 64ECh. 3.2 - Prob. 65ECh. 3.2 - Prob. 66ECh. 3.2 - Prob. 67ECh. 3.2 - Prob. 68ECh. 3.2 - Prob. 69ECh. 3.2 - Prob. 70ECh. 3.2 - Prob. 71ECh. 3.2 - Prob. 72ECh. 3.2 - Prob. 73ECh. 3.2 - Prob. 74ECh. 3.2 - Prob. 75ECh. 3.2 - Prob. 76ECh. 3.2 - Prob. 77ECh. 3.2 - Prob. 78ECh. 3.2 - Prob. 79ECh. 3.2 - Prob. 80ECh. 3.2 - Prob. 81ECh. 3.2 - Prob. 82ECh. 3.2 - Prob. 83ECh. 3.2 - Prob. 84ECh. 3.2 - Prob. 85ECh. 3.2 - Prob. 86ECh. 3.2 - Prob. 87ECh. 3.2 - Prob. 88ECh. 3.2 - Prob. 89ECh. 3.2 - Prob. 90ECh. 3.2 - Prob. 91ECh. 3.2 - Prob. 92ECh. 3.3 - Prob. 1ECh. 3.3 - Prob. 2ECh. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Prob. 5ECh. 3.3 - Prob. 6ECh. 3.3 - Prob. 7ECh. 3.3 - Prob. 8ECh. 3.3 - Prob. 9ECh. 3.3 - Prob. 10ECh. 3.3 - Prob. 11ECh. 3.3 - Prob. 12ECh. 3.3 - Prob. 13ECh. 3.3 - Prob. 14ECh. 3.3 - Prob. 15ECh. 3.3 - Prob. 16ECh. 3.3 - Prob. 17ECh. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Prob. 20ECh. 3.3 - Prob. 21ECh. 3.3 - Prob. 22ECh. 3.3 - Prob. 23ECh. 3.3 - Prob. 24ECh. 3.3 - Prob. 25ECh. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - Prob. 29ECh. 3.3 - Prob. 30ECh. 3.3 - Prob. 31ECh. 3.3 - Prob. 32ECh. 3.3 - Prob. 33ECh. 3.3 - Prob. 34ECh. 3.3 - Prob. 35ECh. 3.3 - Prob. 36ECh. 3.3 - Prob. 37ECh. 3.3 - Prob. 38ECh. 3.3 - Prob. 39ECh. 3.3 - Prob. 40ECh. 3.3 - Prob. 41ECh. 3.3 - Prob. 42ECh. 3.3 - Prob. 43ECh. 3.3 - Prob. 44ECh. 3.3 - Prob. 45ECh. 3.3 - Prob. 46ECh. 3.3 - Prob. 47ECh. 3.3 - Prob. 48ECh. 3.3 - Prob. 49ECh. 3.3 - Prob. 50ECh. 3.3 - Prob. 51ECh. 3.3 - Prob. 52ECh. 3.3 - Prob. 53ECh. 3.3 - Prob. 54ECh. 3.3 - Prob. 55ECh. 3.3 - Prob. 56ECh. 3.3 - Prob. 57ECh. 3.3 - Prob. 58ECh. 3.3 - Prob. 59ECh. 3.3 - Prob. 60ECh. 3.3 - Prob. 61ECh. 3.3 - Prob. 62ECh. 3.3 - Prob. 63ECh. 3.3 - Prob. 64ECh. 3.3 - Prob. 65ECh. 3.3 - Prob. 66ECh. 3.3 - Prob. 67ECh. 3.3 - Prob. 68ECh. 3.3 - Prob. 69ECh. 3.3 - Prob. 70ECh. 3.3 - Prob. 71ECh. 3.3 - Prob. 72ECh. 3.3 - Prob. 73ECh. 3.3 - Prob. 74ECh. 3.3 - Prob. 75ECh. 3.3 - Prob. 76ECh. 3.3 - Prob. 77ECh. 3.3 - Prob. 78ECh. 3.3 - Prob. 79ECh. 3.3 - Prob. 80ECh. 3.3 - Prob. 81ECh. 3.3 - Prob. 82ECh. 3.3 - Prob. 83ECh. 3.3 - Prob. 84ECh. 3.3 - Prob. 85ECh. 3.3 - Prob. 86ECh. 3.3 - Prob. 87ECh. 3.3 - Prob. 88ECh. 3.3 - Prob. 89ECh. 3.3 - Prob. 90ECh. 3.3 - Prob. 91ECh. 3.3 - Prob. 92ECh. 3.3 - Prob. 93ECh. 3.3 - Prob. 94ECh. 3.3 - Prob. 95ECh. 3.3 - Prob. 96ECh. 3.3 - Prob. 97ECh. 3.3 - Prob. 98ECh. 3.3 - Prob. 99ECh. 3.3 - Prob. 100ECh. 3.3 - Prob. 101ECh. 3.3 - Prob. 102ECh. 3.3 - Prob. 103ECh. 3.3 - Prob. 104ECh. 3.3 - Prob. 105ECh. 3.4 - Prob. 1ECh. 3.4 - Prob. 2ECh. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - Prob. 13ECh. 3.4 - Prob. 14ECh. 3.4 - Prob. 15ECh. 3.4 - Prob. 16ECh. 3.4 - Prob. 17ECh. 3.4 - Prob. 18ECh. 3.4 - Prob. 19ECh. 3.4 - Prob. 20ECh. 3.4 - Prob. 21ECh. 3.4 - Prob. 22ECh. 3.4 - Prob. 23ECh. 3.4 - Prob. 24ECh. 3.4 - Prob. 25ECh. 3.4 - Prob. 26ECh. 3.4 - Prob. 27ECh. 3.4 - Prob. 28ECh. 3.4 - Prob. 29ECh. 3.4 - Prob. 30ECh. 3.4 - Prob. 31ECh. 3.4 - Prob. 32ECh. 3.4 - Prob. 33ECh. 3.4 - Prob. 34ECh. 3.4 - Prob. 35ECh. 3.4 - Prob. 36ECh. 3.4 - Prob. 37ECh. 3.4 - Prob. 38ECh. 3.4 - Prob. 39ECh. 3.4 - Prob. 40ECh. 3.4 - Prob. 41ECh. 3.4 - Prob. 42ECh. 3.4 - Prob. 43ECh. 3.4 - Prob. 44ECh. 3.4 - Prob. 45ECh. 3.4 - Prob. 46ECh. 3.4 - Prob. 47ECh. 3.4 - Prob. 48ECh. 3.4 - Prob. 49ECh. 3.4 - Prob. 50ECh. 3.4 - Prob. 51ECh. 3.4 - Prob. 52ECh. 3.4 - Prob. 53ECh. 3.4 - Prob. 54ECh. 3.4 - Prob. 55ECh. 3.4 - Prob. 56ECh. 3.4 - Prob. 57ECh. 3.4 - Prob. 58ECh. 3.4 - Prob. 59ECh. 3.4 - Prob. 60ECh. 3.4 - Prob. 61ECh. 3.4 - Prob. 62ECh. 3.4 - Prob. 63ECh. 3.4 - Prob. 64ECh. 3.4 - Prob. 65ECh. 3.4 - Prob. 66ECh. 3.4 - Prob. 67ECh. 3.4 - Prob. 68ECh. 3.4 - Prob. 69ECh. 3.4 - Prob. 70ECh. 3.4 - Prob. 71ECh. 3.4 - Prob. 72ECh. 3.4 - Prob. 73ECh. 3.4 - Prob. 74ECh. 3.4 - Prob. 75ECh. 3.4 - Prob. 76ECh. 3.4 - Prob. 77ECh. 3.4 - Prob. 78ECh. 3.4 - Prob. 79ECh. 3.4 - Prob. 80ECh. 3.4 - Prob. 81ECh. 3.4 - Prob. 82ECh. 3.4 - Prob. 83ECh. 3.4 - Prob. 84ECh. 3.4 - Prob. 85ECh. 3.4 - Prob. 86ECh. 3.4 - Prob. 87ECh. 3.4 - Prob. 88ECh. 3.4 - Prob. 89ECh. 3.4 - Prob. 90ECh. 3.4 - Prob. 91ECh. 3.4 - Prob. 92ECh. 3.4 - Prob. 93ECh. 3.4 - Prob. 94ECh. 3.4 - Prob. 95ECh. 3.4 - Prob. 96ECh. 3.4 - Prob. 97ECh. 3.4 - Prob. 98ECh. 3.5 - Prob. 1ECh. 3.5 - Prob. 2ECh. 3.5 - Prob. 3ECh. 3.5 - Prob. 4ECh. 3.5 - Prob. 5ECh. 3.5 - Prob. 6ECh. 3.5 - Prob. 7ECh. 3.5 - Prob. 8ECh. 3.5 - Prob. 9ECh. 3.5 - Prob. 10ECh. 3.5 - Prob. 11ECh. 3.5 - Prob. 12ECh. 3.5 - Prob. 13ECh. 3.5 - Prob. 14ECh. 3.5 - Prob. 15ECh. 3.5 - Prob. 16ECh. 3.5 - Prob. 17ECh. 3.5 - Prob. 18ECh. 3.5 - Prob. 19ECh. 3.5 - Prob. 20ECh. 3.5 - Prob. 21ECh. 3.5 - Prob. 22ECh. 3.5 - Prob. 23ECh. 3.5 - Prob. 24ECh. 3.5 - Prob. 25ECh. 3.5 - Prob. 26ECh. 3.5 - Prob. 27ECh. 3.5 - Prob. 28ECh. 3.5 - Prob. 29ECh. 3.5 - Prob. 30ECh. 3.5 - Prob. 31ECh. 3.5 - Prob. 32ECh. 3.5 - Prob. 33ECh. 3.5 - Prob. 34ECh. 3.5 - Prob. 35ECh. 3.5 - Prob. 36ECh. 3.5 - Prob. 37ECh. 3.5 - Prob. 38ECh. 3.5 - Prob. 39ECh. 3.5 - Prob. 40ECh. 3.5 - Prob. 41ECh. 3.5 - Prob. 42ECh. 3.5 - Prob. 43ECh. 3.5 - Prob. 44ECh. 3.5 - Prob. 45ECh. 3.5 - Prob. 46ECh. 3.5 - Prob. 47ECh. 3.5 - Prob. 48ECh. 3.5 - Prob. 49ECh. 3.5 - Prob. 50ECh. 3.5 - Prob. 51ECh. 3.5 - Prob. 52ECh. 3.5 - Prob. 53ECh. 3.5 - Prob. 54ECh. 3.5 - Prob. 55ECh. 3.5 - Prob. 56ECh. 3.5 - Prob. 57ECh. 3.5 - Prob. 58ECh. 3.5 - Prob. 59ECh. 3.5 - Prob. 60ECh. 3.5 - Prob. 61ECh. 3.5 - Prob. 62ECh. 3.5 - Prob. 63ECh. 3.5 - Prob. 64ECh. 3.5 - Prob. 65ECh. 3.5 - Prob. 66ECh. 3 - Prob. 1RECh. 3 - Prob. 2RECh. 3 - Prob. 3RECh. 3 - Prob. 4RECh. 3 - Prob. 5RECh. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Prob. 8RECh. 3 - Prob. 9RECh. 3 - Prob. 10RECh. 3 - Prob. 11RECh. 3 - Prob. 12RECh. 3 - Prob. 13RECh. 3 - Prob. 14RECh. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - Prob. 17RECh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 - Prob. 21RECh. 3 - Prob. 22RECh. 3 - Prob. 23RECh. 3 - Prob. 24RECh. 3 - Prob. 25RECh. 3 - Prob. 26RECh. 3 - Prob. 27RECh. 3 - Prob. 28RECh. 3 - Prob. 29RECh. 3 - Prob. 30RECh. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - Prob. 33RECh. 3 - Prob. 34RECh. 3 - Prob. 35RECh. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Prob. 38RECh. 3 - Prob. 39RECh. 3 - Prob. 40RECh. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Prob. 43RECh. 3 - Prob. 44RECh. 3 - Prob. 45RECh. 3 - Prob. 46RECh. 3 - Prob. 47RECh. 3 - Prob. 48RECh. 3 - Prob. 49RECh. 3 - Prob. 50RECh. 3 - Prob. 51RECh. 3 - Prob. 52RECh. 3 - Prob. 53RECh. 3 - Prob. 54RECh. 3 - Prob. 55RECh. 3 - Prob. 56RECh. 3 - Prob. 57RECh. 3 - Prob. 58RECh. 3 - Prob. 59RECh. 3 - Prob. 60RECh. 3 - Prob. 61RECh. 3 - Prob. 62RECh. 3 - Prob. 63RECh. 3 - Prob. 64RECh. 3 - Prob. 65RECh. 3 - Prob. 66RECh. 3 - Prob. 67RECh. 3 - Prob. 68RECh. 3 - Prob. 69RECh. 3 - Prob. 70RECh. 3 - Prob. 71RECh. 3 - Prob. 72RECh. 3 - Prob. 73RECh. 3 - Prob. 74RECh. 3 - Prob. 75RECh. 3 - Prob. 76RECh. 3 - Prob. 77RECh. 3 - Prob. 78RECh. 3 - Prob. 79RECh. 3 - Prob. 80RECh. 3 - Prob. 81RECh. 3 - Prob. 82RECh. 3 - Prob. 83RECh. 3 - Prob. 84RECh. 3 - Prob. 85RECh. 3 - Prob. 86RECh. 3 - Prob. 87RECh. 3 - Prob. 88RECh. 3 - Prob. 89RECh. 3 - Prob. 90RECh. 3 - Prob. 91RECh. 3 - Prob. 92RECh. 3 - Prob. 93RECh. 3 - Prob. 94RECh. 3 - Prob. 95RECh. 3 - Prob. 96RECh. 3 - Prob. 97RECh. 3 - Prob. 98RECh. 3 - Prob. 99RECh. 3 - Prob. 100RECh. 3 - Prob. 101RECh. 3 - Prob. 102RECh. 3 - Prob. 103RECh. 3 - Prob. 104RECh. 3 - Prob. 105RECh. 3 - Prob. 106RECh. 3 - Prob. 107RECh. 3 - Prob. 108RECh. 3 - Prob. 109RECh. 3 - Prob. 110RECh. 3 - Prob. 111RECh. 3 - Prob. 112RECh. 3 - Prob. 113RECh. 3 - Prob. 114RECh. 3 - Prob. 115RECh. 3 - Prob. 116RECh. 3 - Prob. 117RECh. 3 - Prob. 118RECh. 3 - Prob. 1CTCh. 3 - Prob. 2CTCh. 3 - Prob. 3CTCh. 3 - Prob. 4CTCh. 3 - Prob. 5CTCh. 3 - Prob. 6CTCh. 3 - Prob. 7CTCh. 3 - Prob. 8CTCh. 3 - Prob. 9CTCh. 3 - Prob. 10CTCh. 3 - Prob. 11CTCh. 3 - Prob. 12CTCh. 3 - Prob. 13CTCh. 3 - Prob. 14CTCh. 3 - Prob. 15CTCh. 3 - Prob. 16CTCh. 3 - Prob. 17CTCh. 3 - Prob. 18CTCh. 3 - Prob. 19CTCh. 3 - Prob. 20CTCh. 3 - Prob. 21CTCh. 3 - Prob. 22CTCh. 3 - Prob. 23CTCh. 3 - Prob. 24CTCh. 3 - Prob. 25CTCh. 3 - Prob. 26CTCh. 3 - Prob. 27CTCh. 3 - Prob. 28CTCh. 3 - Prob. 29CTCh. 3 - Prob. 1CLTCh. 3 - Prob. 2CLTCh. 3 - Prob. 3CLTCh. 3 - Prob. 4CLTCh. 3 - Prob. 5CLTCh. 3 - Prob. 6CLTCh. 3 - Prob. 7CLTCh. 3 - Prob. 8CLTCh. 3 - Prob. 9CLTCh. 3 - Prob. 10CLTCh. 3 - Prob. 11CLTCh. 3 - Prob. 12CLTCh. 3 - Prob. 13CLTCh. 3 - Prob. 14CLTCh. 3 - Prob. 15CLTCh. 3 - Prob. 16CLTCh. 3 - Prob. 17CLTCh. 3 - Prob. 18CLTCh. 3 - Prob. 19CLTCh. 3 - Prob. 20CLTCh. 3 - Prob. 21CLTCh. 3 - Prob. 22CLTCh. 3 - Prob. 23CLTCh. 3 - Prob. 24CLTCh. 3 - Prob. 25CLTCh. 3 - Prob. 26CLTCh. 3 - Prob. 27CLTCh. 3 - Prob. 28CLTCh. 3 - Prob. 29CLTCh. 3 - Prob. 30CLTCh. 3 - Prob. 31CLTCh. 3 - Prob. 32CLTCh. 3 - Prob. 33CLTCh. 3 - Prob. 34CLTCh. 3 - Prob. 35CLTCh. 3 - Prob. 36CLTCh. 3 - Prob. 37CLTCh. 3 - Prob. 38CLTCh. 3 - Prob. 39CLTCh. 3 - Prob. 40CLTCh. 3 - Prob. 41CLTCh. 3 - Prob. 42CLTCh. 3 - Prob. 43CLTCh. 3 - Prob. 1PSCh. 3 - Prob. 2PSCh. 3 - Prob. 3PSCh. 3 - Prob. 4PSCh. 3 - Prob. 5PSCh. 3 - Prob. 6PSCh. 3 - Prob. 7PSCh. 3 - Prob. 8PSCh. 3 - Prob. 9PSCh. 3 - Prob. 10PSCh. 3 - Prob. 11PSCh. 3 - Prob. 12PSCh. 3 - Prob. 13PSCh. 3 - Prob. 14PSCh. 3 - Prob. 15PSCh. 3 - Prob. 16PSCh. 3 - Prob. 17PSCh. 3 - Prob. 18PSCh. 3 - Prob. 19PSCh. 3 - Prob. 20PSCh. 3 - Prob. 21PSCh. 3 - Prob. 22PSCh. 3 - Prob. 23PSCh. 3 - Prob. 24PSCh. 3 - Prob. 25PSCh. 3 - Prob. 26PS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Solve by DrWz WI P L B dy Sind Ⓡ de max ⑦Ymax dx Solve by Dr ③Yat 0.75m from A w=6KN/M L=2 W2=9 kN/m P= 10 KN Solve By Drarrow_forwardHow to find the radius of convergence for the series in the image below? I'm stuck on how to isolate the x in the interval of convergence.arrow_forwardDetermine the exact signed area between the curve g(x): x-axis on the interval [0,1]. = tan2/5 secx dx andarrow_forward
- A factorization A = PDP 1 is not unique. For A= 7 2 -4 1 1 1 5 0 2 1 one factorization is P = D= and P-1 30 = Use this information with D₁ = to find a matrix P₁ such that - -1 -2 0 3 1 - - 1 05 A-P,D,P P1 (Type an integer or simplified fraction for each matrix element.)arrow_forwardMatrix A is factored in the form PDP 1. Use the Diagonalization Theorem to find the eigenvalues of A and a basis for each eigenspace. 30 -1 - 1 0 -1 400 0 0 1 A= 3 4 3 0 1 3 040 3 1 3 0 0 4 1 0 0 003 -1 0 -1 Select the correct choice below and fill in the answer boxes to complete your choice. (Use a comma to separate vectors as needed.) A basis for the corresponding eigenspace is { A. There is one distinct eigenvalue, λ = B. In ascending order, the two distinct eigenvalues are λ₁ ... = and 2 = Bases for the corresponding eigenspaces are { and ( ), respectively. C. In ascending order, the three distinct eigenvalues are λ₁ = = 12/2 = and 3 = Bases for the corresponding eigenspaces are {}, }, and { respectively.arrow_forwardN Page 0.6. 0.4. 0.2- -0.2- -0.4- -6.6 -5 W 10arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Implicit Differentiation with Transcendental Functions; Author: Mathispower4u;https://www.youtube.com/watch?v=16WoO59R88w;License: Standard YouTube License, CC-BY
How to determine the difference between an algebraic and transcendental expression; Author: Study Force;https://www.youtube.com/watch?v=xRht10w7ZOE;License: Standard YouTube License, CC-BY