EBK PRECALCULUS W/LIMITS
4th Edition
ISBN: 9781337516853
Author: Larson
Publisher: CENGAGE CO
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 3.2, Problem 45E
To determine
To find the domain, x - intercepts, vertical asymptotes and to sketch the graph of the function
f(x)=−log6(x+2) .
Expert Solution & Answer
Answer to Problem 45E
(−2,∞)
Explanation of Solution
Given:
Function: f(x)=−log6(x+2)
Formula used:
logab=c⇔b=ac
Calculation:
Finding the domain of the function,
When x>−2 , the function is defined.
So, the domain of the function is (−2,∞).
To find the x-intercept, put f(x)=y=0 in given function.
⇒0=−log6(x+2)⇒0=log6(x+2)⇒x+2=60 [∵logab=c⇔b=ac]⇒x+2=1⇒x=1−2⇒x=−1
So, x-intercept is (−1,0) .
Asymptotes:
Vertical asymptotes:
To find vertical asymptotes, put the value of the given function in logarithmic part equal to zero.
⇒x+2=0⇒x=−2
So, the vertical asymptote is x=−2.
Calculation for graph:
Consider f(x)=−log6(x+2)
| Values of x | Values of f (x) |
| -1 | 0 |
| 0 | -0.387 |
| 1 | -0.613 |
| 2 | -0.774 |
By taking different values of x, the graph can be plotted.
Graph:
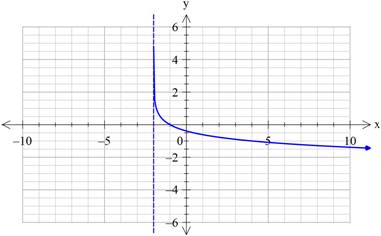
Interpretation:
The above graph represents the sketch of given function.
Chapter 3 Solutions
EBK PRECALCULUS W/LIMITS
Ch. 3.1 - Prob. 1ECh. 3.1 - Prob. 2ECh. 3.1 - Prob. 3ECh. 3.1 - Prob. 4ECh. 3.1 - Prob. 5ECh. 3.1 - Prob. 6ECh. 3.1 - Prob. 7ECh. 3.1 - Prob. 8ECh. 3.1 - Prob. 9ECh. 3.1 - Prob. 10E
Ch. 3.1 - Prob. 11ECh. 3.1 - Prob. 12ECh. 3.1 - Prob. 13ECh. 3.1 - Prob. 14ECh. 3.1 - Prob. 15ECh. 3.1 - Prob. 16ECh. 3.1 - Prob. 17ECh. 3.1 - Prob. 18ECh. 3.1 - Prob. 19ECh. 3.1 - Prob. 20ECh. 3.1 - Prob. 21ECh. 3.1 - Prob. 22ECh. 3.1 - Prob. 23ECh. 3.1 - Prob. 24ECh. 3.1 - Prob. 25ECh. 3.1 - Prob. 26ECh. 3.1 - Prob. 27ECh. 3.1 - Prob. 28ECh. 3.1 - Prob. 29ECh. 3.1 - Prob. 30ECh. 3.1 - Prob. 31ECh. 3.1 - Prob. 32ECh. 3.1 - Prob. 33ECh. 3.1 - Prob. 34ECh. 3.1 - Prob. 35ECh. 3.1 - Prob. 36ECh. 3.1 - Prob. 37ECh. 3.1 - Prob. 38ECh. 3.1 - Prob. 39ECh. 3.1 - Prob. 40ECh. 3.1 - Prob. 41ECh. 3.1 - Prob. 42ECh. 3.1 - Prob. 43ECh. 3.1 - Prob. 44ECh. 3.1 - Prob. 45ECh. 3.1 - Prob. 46ECh. 3.1 - Prob. 47ECh. 3.1 - Prob. 48ECh. 3.1 - Prob. 49ECh. 3.1 - Prob. 50ECh. 3.1 - Prob. 51ECh. 3.1 - Prob. 52ECh. 3.1 - Prob. 53ECh. 3.1 - Prob. 54ECh. 3.1 - Prob. 55ECh. 3.1 - Prob. 56ECh. 3.1 - Prob. 57ECh. 3.1 - Prob. 58ECh. 3.1 - Prob. 59ECh. 3.1 - Prob. 60ECh. 3.1 - Prob. 61ECh. 3.1 - Prob. 62ECh. 3.1 - Prob. 63ECh. 3.1 - Prob. 64ECh. 3.1 - Prob. 65ECh. 3.1 - Prob. 66ECh. 3.1 - Prob. 67ECh. 3.1 - Prob. 68ECh. 3.1 - Prob. 69ECh. 3.1 - Prob. 70ECh. 3.1 - Prob. 71ECh. 3.1 - Prob. 72ECh. 3.1 - Prob. 73ECh. 3.1 - Prob. 74ECh. 3.1 - Prob. 75ECh. 3.1 - Prob. 76ECh. 3.1 - Prob. 77ECh. 3.1 - Prob. 78ECh. 3.1 - Prob. 79ECh. 3.1 - Prob. 80ECh. 3.2 - Prob. 1ECh. 3.2 - Prob. 2ECh. 3.2 - Prob. 3ECh. 3.2 - Prob. 4ECh. 3.2 - Prob. 5ECh. 3.2 - Prob. 6ECh. 3.2 - Prob. 7ECh. 3.2 - Prob. 8ECh. 3.2 - Prob. 9ECh. 3.2 - Prob. 10ECh. 3.2 - Prob. 11ECh. 3.2 - Prob. 12ECh. 3.2 - Prob. 13ECh. 3.2 - Prob. 14ECh. 3.2 - Prob. 15ECh. 3.2 - Prob. 16ECh. 3.2 - Prob. 17ECh. 3.2 - Prob. 18ECh. 3.2 - Prob. 19ECh. 3.2 - Prob. 20ECh. 3.2 - Prob. 21ECh. 3.2 - Prob. 22ECh. 3.2 - Prob. 23ECh. 3.2 - Prob. 24ECh. 3.2 - Prob. 25ECh. 3.2 - Prob. 26ECh. 3.2 - Prob. 27ECh. 3.2 - Prob. 28ECh. 3.2 - Prob. 29ECh. 3.2 - Prob. 30ECh. 3.2 - Prob. 31ECh. 3.2 - Prob. 32ECh. 3.2 - Prob. 33ECh. 3.2 - Prob. 34ECh. 3.2 - Prob. 35ECh. 3.2 - Prob. 36ECh. 3.2 - Prob. 37ECh. 3.2 - Prob. 38ECh. 3.2 - Prob. 39ECh. 3.2 - Prob. 40ECh. 3.2 - Prob. 41ECh. 3.2 - Prob. 42ECh. 3.2 - Prob. 43ECh. 3.2 - Prob. 44ECh. 3.2 - Prob. 45ECh. 3.2 - Prob. 46ECh. 3.2 - Prob. 47ECh. 3.2 - Prob. 48ECh. 3.2 - Prob. 49ECh. 3.2 - Prob. 50ECh. 3.2 - Prob. 51ECh. 3.2 - Prob. 52ECh. 3.2 - Prob. 53ECh. 3.2 - Prob. 54ECh. 3.2 - Prob. 55ECh. 3.2 - Prob. 56ECh. 3.2 - Prob. 57ECh. 3.2 - Prob. 58ECh. 3.2 - Prob. 59ECh. 3.2 - Prob. 60ECh. 3.2 - Prob. 61ECh. 3.2 - Prob. 62ECh. 3.2 - Prob. 63ECh. 3.2 - Prob. 64ECh. 3.2 - Prob. 65ECh. 3.2 - Prob. 66ECh. 3.2 - Prob. 67ECh. 3.2 - Prob. 68ECh. 3.2 - Prob. 69ECh. 3.2 - Prob. 70ECh. 3.2 - Prob. 71ECh. 3.2 - Prob. 72ECh. 3.2 - Prob. 73ECh. 3.2 - Prob. 74ECh. 3.2 - Prob. 75ECh. 3.2 - Prob. 76ECh. 3.2 - Prob. 77ECh. 3.2 - Prob. 78ECh. 3.2 - Prob. 79ECh. 3.2 - Prob. 80ECh. 3.2 - Prob. 81ECh. 3.2 - Prob. 82ECh. 3.2 - Prob. 83ECh. 3.2 - Prob. 84ECh. 3.2 - Prob. 85ECh. 3.2 - Prob. 86ECh. 3.2 - Prob. 87ECh. 3.2 - Prob. 88ECh. 3.2 - Prob. 89ECh. 3.2 - Prob. 90ECh. 3.2 - Prob. 91ECh. 3.2 - Prob. 92ECh. 3.3 - Prob. 1ECh. 3.3 - Prob. 2ECh. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Prob. 5ECh. 3.3 - Prob. 6ECh. 3.3 - Prob. 7ECh. 3.3 - Prob. 8ECh. 3.3 - Prob. 9ECh. 3.3 - Prob. 10ECh. 3.3 - Prob. 11ECh. 3.3 - Prob. 12ECh. 3.3 - Prob. 13ECh. 3.3 - Prob. 14ECh. 3.3 - Prob. 15ECh. 3.3 - Prob. 16ECh. 3.3 - Prob. 17ECh. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Prob. 20ECh. 3.3 - Prob. 21ECh. 3.3 - Prob. 22ECh. 3.3 - Prob. 23ECh. 3.3 - Prob. 24ECh. 3.3 - Prob. 25ECh. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - Prob. 29ECh. 3.3 - Prob. 30ECh. 3.3 - Prob. 31ECh. 3.3 - Prob. 32ECh. 3.3 - Prob. 33ECh. 3.3 - Prob. 34ECh. 3.3 - Prob. 35ECh. 3.3 - Prob. 36ECh. 3.3 - Prob. 37ECh. 3.3 - Prob. 38ECh. 3.3 - Prob. 39ECh. 3.3 - Prob. 40ECh. 3.3 - Prob. 41ECh. 3.3 - Prob. 42ECh. 3.3 - Prob. 43ECh. 3.3 - Prob. 44ECh. 3.3 - Prob. 45ECh. 3.3 - Prob. 46ECh. 3.3 - Prob. 47ECh. 3.3 - Prob. 48ECh. 3.3 - Prob. 49ECh. 3.3 - Prob. 50ECh. 3.3 - Prob. 51ECh. 3.3 - Prob. 52ECh. 3.3 - Prob. 53ECh. 3.3 - Prob. 54ECh. 3.3 - Prob. 55ECh. 3.3 - Prob. 56ECh. 3.3 - Prob. 57ECh. 3.3 - Prob. 58ECh. 3.3 - Prob. 59ECh. 3.3 - Prob. 60ECh. 3.3 - Prob. 61ECh. 3.3 - Prob. 62ECh. 3.3 - Prob. 63ECh. 3.3 - Prob. 64ECh. 3.3 - Prob. 65ECh. 3.3 - Prob. 66ECh. 3.3 - Prob. 67ECh. 3.3 - Prob. 68ECh. 3.3 - Prob. 69ECh. 3.3 - Prob. 70ECh. 3.3 - Prob. 71ECh. 3.3 - Prob. 72ECh. 3.3 - Prob. 73ECh. 3.3 - Prob. 74ECh. 3.3 - Prob. 75ECh. 3.3 - Prob. 76ECh. 3.3 - Prob. 77ECh. 3.3 - Prob. 78ECh. 3.3 - Prob. 79ECh. 3.3 - Prob. 80ECh. 3.3 - Prob. 81ECh. 3.3 - Prob. 82ECh. 3.3 - Prob. 83ECh. 3.3 - Prob. 84ECh. 3.3 - Prob. 85ECh. 3.3 - Prob. 86ECh. 3.3 - Prob. 87ECh. 3.3 - Prob. 88ECh. 3.3 - Prob. 89ECh. 3.3 - Prob. 90ECh. 3.3 - Prob. 91ECh. 3.3 - Prob. 92ECh. 3.3 - Prob. 93ECh. 3.3 - Prob. 94ECh. 3.3 - Prob. 95ECh. 3.3 - Prob. 96ECh. 3.3 - Prob. 97ECh. 3.3 - Prob. 98ECh. 3.3 - Prob. 99ECh. 3.3 - Prob. 100ECh. 3.3 - Prob. 101ECh. 3.3 - Prob. 102ECh. 3.3 - Prob. 103ECh. 3.3 - Prob. 104ECh. 3.3 - Prob. 105ECh. 3.4 - Prob. 1ECh. 3.4 - Prob. 2ECh. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - Prob. 13ECh. 3.4 - Prob. 14ECh. 3.4 - Prob. 15ECh. 3.4 - Prob. 16ECh. 3.4 - Prob. 17ECh. 3.4 - Prob. 18ECh. 3.4 - Prob. 19ECh. 3.4 - Prob. 20ECh. 3.4 - Prob. 21ECh. 3.4 - Prob. 22ECh. 3.4 - Prob. 23ECh. 3.4 - Prob. 24ECh. 3.4 - Prob. 25ECh. 3.4 - Prob. 26ECh. 3.4 - Prob. 27ECh. 3.4 - Prob. 28ECh. 3.4 - Prob. 29ECh. 3.4 - Prob. 30ECh. 3.4 - Prob. 31ECh. 3.4 - Prob. 32ECh. 3.4 - Prob. 33ECh. 3.4 - Prob. 34ECh. 3.4 - Prob. 35ECh. 3.4 - Prob. 36ECh. 3.4 - Prob. 37ECh. 3.4 - Prob. 38ECh. 3.4 - Prob. 39ECh. 3.4 - Prob. 40ECh. 3.4 - Prob. 41ECh. 3.4 - Prob. 42ECh. 3.4 - Prob. 43ECh. 3.4 - Prob. 44ECh. 3.4 - Prob. 45ECh. 3.4 - Prob. 46ECh. 3.4 - Prob. 47ECh. 3.4 - Prob. 48ECh. 3.4 - Prob. 49ECh. 3.4 - Prob. 50ECh. 3.4 - Prob. 51ECh. 3.4 - Prob. 52ECh. 3.4 - Prob. 53ECh. 3.4 - Prob. 54ECh. 3.4 - Prob. 55ECh. 3.4 - Prob. 56ECh. 3.4 - Prob. 57ECh. 3.4 - Prob. 58ECh. 3.4 - Prob. 59ECh. 3.4 - Prob. 60ECh. 3.4 - Prob. 61ECh. 3.4 - Prob. 62ECh. 3.4 - Prob. 63ECh. 3.4 - Prob. 64ECh. 3.4 - Prob. 65ECh. 3.4 - Prob. 66ECh. 3.4 - Prob. 67ECh. 3.4 - Prob. 68ECh. 3.4 - Prob. 69ECh. 3.4 - Prob. 70ECh. 3.4 - Prob. 71ECh. 3.4 - Prob. 72ECh. 3.4 - Prob. 73ECh. 3.4 - Prob. 74ECh. 3.4 - Prob. 75ECh. 3.4 - Prob. 76ECh. 3.4 - Prob. 77ECh. 3.4 - Prob. 78ECh. 3.4 - Prob. 79ECh. 3.4 - Prob. 80ECh. 3.4 - Prob. 81ECh. 3.4 - Prob. 82ECh. 3.4 - Prob. 83ECh. 3.4 - Prob. 84ECh. 3.4 - Prob. 85ECh. 3.4 - Prob. 86ECh. 3.4 - Prob. 87ECh. 3.4 - Prob. 88ECh. 3.4 - Prob. 89ECh. 3.4 - Prob. 90ECh. 3.4 - Prob. 91ECh. 3.4 - Prob. 92ECh. 3.4 - Prob. 93ECh. 3.4 - Prob. 94ECh. 3.4 - Prob. 95ECh. 3.4 - Prob. 96ECh. 3.4 - Prob. 97ECh. 3.4 - Prob. 98ECh. 3.5 - Prob. 1ECh. 3.5 - Prob. 2ECh. 3.5 - Prob. 3ECh. 3.5 - Prob. 4ECh. 3.5 - Prob. 5ECh. 3.5 - Prob. 6ECh. 3.5 - Prob. 7ECh. 3.5 - Prob. 8ECh. 3.5 - Prob. 9ECh. 3.5 - Prob. 10ECh. 3.5 - Prob. 11ECh. 3.5 - Prob. 12ECh. 3.5 - Prob. 13ECh. 3.5 - Prob. 14ECh. 3.5 - Prob. 15ECh. 3.5 - Prob. 16ECh. 3.5 - Prob. 17ECh. 3.5 - Prob. 18ECh. 3.5 - Prob. 19ECh. 3.5 - Prob. 20ECh. 3.5 - Prob. 21ECh. 3.5 - Prob. 22ECh. 3.5 - Prob. 23ECh. 3.5 - Prob. 24ECh. 3.5 - Prob. 25ECh. 3.5 - Prob. 26ECh. 3.5 - Prob. 27ECh. 3.5 - Prob. 28ECh. 3.5 - Prob. 29ECh. 3.5 - Prob. 30ECh. 3.5 - Prob. 31ECh. 3.5 - Prob. 32ECh. 3.5 - Prob. 33ECh. 3.5 - Prob. 34ECh. 3.5 - Prob. 35ECh. 3.5 - Prob. 36ECh. 3.5 - Prob. 37ECh. 3.5 - Prob. 38ECh. 3.5 - Prob. 39ECh. 3.5 - Prob. 40ECh. 3.5 - Prob. 41ECh. 3.5 - Prob. 42ECh. 3.5 - Prob. 43ECh. 3.5 - Prob. 44ECh. 3.5 - Prob. 45ECh. 3.5 - Prob. 46ECh. 3.5 - Prob. 47ECh. 3.5 - Prob. 48ECh. 3.5 - Prob. 49ECh. 3.5 - Prob. 50ECh. 3.5 - Prob. 51ECh. 3.5 - Prob. 52ECh. 3.5 - Prob. 53ECh. 3.5 - Prob. 54ECh. 3.5 - Prob. 55ECh. 3.5 - Prob. 56ECh. 3.5 - Prob. 57ECh. 3.5 - Prob. 58ECh. 3.5 - Prob. 59ECh. 3.5 - Prob. 60ECh. 3.5 - Prob. 61ECh. 3.5 - Prob. 62ECh. 3.5 - Prob. 63ECh. 3.5 - Prob. 64ECh. 3.5 - Prob. 65ECh. 3.5 - Prob. 66ECh. 3 - Prob. 1RECh. 3 - Prob. 2RECh. 3 - Prob. 3RECh. 3 - Prob. 4RECh. 3 - Prob. 5RECh. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Prob. 8RECh. 3 - Prob. 9RECh. 3 - Prob. 10RECh. 3 - Prob. 11RECh. 3 - Prob. 12RECh. 3 - Prob. 13RECh. 3 - Prob. 14RECh. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - Prob. 17RECh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 - Prob. 21RECh. 3 - Prob. 22RECh. 3 - Prob. 23RECh. 3 - Prob. 24RECh. 3 - Prob. 25RECh. 3 - Prob. 26RECh. 3 - Prob. 27RECh. 3 - Prob. 28RECh. 3 - Prob. 29RECh. 3 - Prob. 30RECh. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - Prob. 33RECh. 3 - Prob. 34RECh. 3 - Prob. 35RECh. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Prob. 38RECh. 3 - Prob. 39RECh. 3 - Prob. 40RECh. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Prob. 43RECh. 3 - Prob. 44RECh. 3 - Prob. 45RECh. 3 - Prob. 46RECh. 3 - Prob. 47RECh. 3 - Prob. 48RECh. 3 - Prob. 49RECh. 3 - Prob. 50RECh. 3 - Prob. 51RECh. 3 - Prob. 52RECh. 3 - Prob. 53RECh. 3 - Prob. 54RECh. 3 - Prob. 55RECh. 3 - Prob. 56RECh. 3 - Prob. 57RECh. 3 - Prob. 58RECh. 3 - Prob. 59RECh. 3 - Prob. 60RECh. 3 - Prob. 61RECh. 3 - Prob. 62RECh. 3 - Prob. 63RECh. 3 - Prob. 64RECh. 3 - Prob. 65RECh. 3 - Prob. 66RECh. 3 - Prob. 67RECh. 3 - Prob. 68RECh. 3 - Prob. 69RECh. 3 - Prob. 70RECh. 3 - Prob. 71RECh. 3 - Prob. 72RECh. 3 - Prob. 73RECh. 3 - Prob. 74RECh. 3 - Prob. 75RECh. 3 - Prob. 76RECh. 3 - Prob. 77RECh. 3 - Prob. 78RECh. 3 - Prob. 79RECh. 3 - Prob. 80RECh. 3 - Prob. 81RECh. 3 - Prob. 82RECh. 3 - Prob. 83RECh. 3 - Prob. 84RECh. 3 - Prob. 85RECh. 3 - Prob. 86RECh. 3 - Prob. 87RECh. 3 - Prob. 88RECh. 3 - Prob. 89RECh. 3 - Prob. 90RECh. 3 - Prob. 91RECh. 3 - Prob. 92RECh. 3 - Prob. 93RECh. 3 - Prob. 94RECh. 3 - Prob. 95RECh. 3 - Prob. 96RECh. 3 - Prob. 97RECh. 3 - Prob. 98RECh. 3 - Prob. 99RECh. 3 - Prob. 100RECh. 3 - Prob. 101RECh. 3 - Prob. 102RECh. 3 - Prob. 103RECh. 3 - Prob. 104RECh. 3 - Prob. 105RECh. 3 - Prob. 106RECh. 3 - Prob. 107RECh. 3 - Prob. 108RECh. 3 - Prob. 109RECh. 3 - Prob. 110RECh. 3 - Prob. 111RECh. 3 - Prob. 112RECh. 3 - Prob. 113RECh. 3 - Prob. 114RECh. 3 - Prob. 115RECh. 3 - Prob. 116RECh. 3 - Prob. 117RECh. 3 - Prob. 118RECh. 3 - Prob. 1CTCh. 3 - Prob. 2CTCh. 3 - Prob. 3CTCh. 3 - Prob. 4CTCh. 3 - Prob. 5CTCh. 3 - Prob. 6CTCh. 3 - Prob. 7CTCh. 3 - Prob. 8CTCh. 3 - Prob. 9CTCh. 3 - Prob. 10CTCh. 3 - Prob. 11CTCh. 3 - Prob. 12CTCh. 3 - Prob. 13CTCh. 3 - Prob. 14CTCh. 3 - Prob. 15CTCh. 3 - Prob. 16CTCh. 3 - Prob. 17CTCh. 3 - Prob. 18CTCh. 3 - Prob. 19CTCh. 3 - Prob. 20CTCh. 3 - Prob. 21CTCh. 3 - Prob. 22CTCh. 3 - Prob. 23CTCh. 3 - Prob. 24CTCh. 3 - Prob. 25CTCh. 3 - Prob. 26CTCh. 3 - Prob. 27CTCh. 3 - Prob. 28CTCh. 3 - Prob. 29CTCh. 3 - Prob. 1CLTCh. 3 - Prob. 2CLTCh. 3 - Prob. 3CLTCh. 3 - Prob. 4CLTCh. 3 - Prob. 5CLTCh. 3 - Prob. 6CLTCh. 3 - Prob. 7CLTCh. 3 - Prob. 8CLTCh. 3 - Prob. 9CLTCh. 3 - Prob. 10CLTCh. 3 - Prob. 11CLTCh. 3 - Prob. 12CLTCh. 3 - Prob. 13CLTCh. 3 - Prob. 14CLTCh. 3 - Prob. 15CLTCh. 3 - Prob. 16CLTCh. 3 - Prob. 17CLTCh. 3 - Prob. 18CLTCh. 3 - Prob. 19CLTCh. 3 - Prob. 20CLTCh. 3 - Prob. 21CLTCh. 3 - Prob. 22CLTCh. 3 - Prob. 23CLTCh. 3 - Prob. 24CLTCh. 3 - Prob. 25CLTCh. 3 - Prob. 26CLTCh. 3 - Prob. 27CLTCh. 3 - Prob. 28CLTCh. 3 - Prob. 29CLTCh. 3 - Prob. 30CLTCh. 3 - Prob. 31CLTCh. 3 - Prob. 32CLTCh. 3 - Prob. 33CLTCh. 3 - Prob. 34CLTCh. 3 - Prob. 35CLTCh. 3 - Prob. 36CLTCh. 3 - Prob. 37CLTCh. 3 - Prob. 38CLTCh. 3 - Prob. 39CLTCh. 3 - Prob. 40CLTCh. 3 - Prob. 41CLTCh. 3 - Prob. 42CLTCh. 3 - Prob. 43CLTCh. 3 - Prob. 1PSCh. 3 - Prob. 2PSCh. 3 - Prob. 3PSCh. 3 - Prob. 4PSCh. 3 - Prob. 5PSCh. 3 - Prob. 6PSCh. 3 - Prob. 7PSCh. 3 - Prob. 8PSCh. 3 - Prob. 9PSCh. 3 - Prob. 10PSCh. 3 - Prob. 11PSCh. 3 - Prob. 12PSCh. 3 - Prob. 13PSCh. 3 - Prob. 14PSCh. 3 - Prob. 15PSCh. 3 - Prob. 16PSCh. 3 - Prob. 17PSCh. 3 - Prob. 18PSCh. 3 - Prob. 19PSCh. 3 - Prob. 20PSCh. 3 - Prob. 21PSCh. 3 - Prob. 22PSCh. 3 - Prob. 23PSCh. 3 - Prob. 24PSCh. 3 - Prob. 25PSCh. 3 - Prob. 26PS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Pls help ASAParrow_forward9. a) Determie values of a and b so that the function is continuous. ax - 2b f(x) 2 x≤-2 -2x+a, x ≥2 \-ax² - bx + 1, −2 < x < 2) 9b) Consider f(x): = 2x²+x-3 x-b and determine all the values of b such that f(x) does not have a vertical asymptote. Show work.arrow_forwardPls help ASAParrow_forward
- 3. True False. If false create functions that prove it is false. Note: f(x) = g(x). a) If_lim ƒ(x) = ∞ and_lim g(x) = ∞,then_lim [ƒ(x) − g(x)] = 0 x→ 0+ x→0+ x→0+ b) If h(x) and g(x) are continuous at x = c, and if h(c) > 0 and g(c) = 0, then h(x) lim. will = x→c g(x) c) If lim f(x) = 0 and lim g(x) = 0 then lim f(x) does not exist. x-a x-a x→a g(x)arrow_forwardPls help ASAParrow_forward15. a) Consider f(x) = x-1 3x+2 and use the difference quotient to determine the simplified expression in terms of x, for the slope of any tangent to y = f(x). Also, determine the slope at x = 2. 15 b) Determine the equation of the tangent to f(x) at x = 2. Final answer in Standard Form Ax + By + C = 0, A ≥ 0, with no fractions or decimals.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Implicit Differentiation with Transcendental Functions; Author: Mathispower4u;https://www.youtube.com/watch?v=16WoO59R88w;License: Standard YouTube License, CC-BY
How to determine the difference between an algebraic and transcendental expression; Author: Study Force;https://www.youtube.com/watch?v=xRht10w7ZOE;License: Standard YouTube License, CC-BY