EBK PRECALCULUS W/LIMITS

4th Edition

ISBN: 9781337516853

Author: Larson

Publisher: CENGAGE CO

See similar textbooks

Concept explainers

Correlation

Correlation defines a relationship between two independent variables. It tells the degree to which variables move in relation to each other. When two sets of data are related to each other, there is a correlation between them.

Linear Correlation

A correlation is used to determine the relationships between numerical and categorical variables. In other words, it is an indicator of how things are connected to one another. The correlation analysis is the study of how variables are related.

Regression Analysis

Regression analysis is a statistical method in which it estimates the relationship between a dependent variable and one or more independent variable. In simple terms dependent variable is called as outcome variable and independent variable is called as p…

Videos

Question

Chapter 3.1, Problem 62E

a .

To determine

To find: is the population of Italy increasing or decreasing.

a .

Expert Solution

Answer to Problem 62E

Increasing

Explanation of Solution

Given:

The population P (in millions) of Italy from 2003 through 2015 can be approximated by the model

P=57.59e0.0051t .................. (1)

Where t represents the year, with t=3 corresponding to 2003.

The graph of the equation P=57.59e0.0051t is given below:

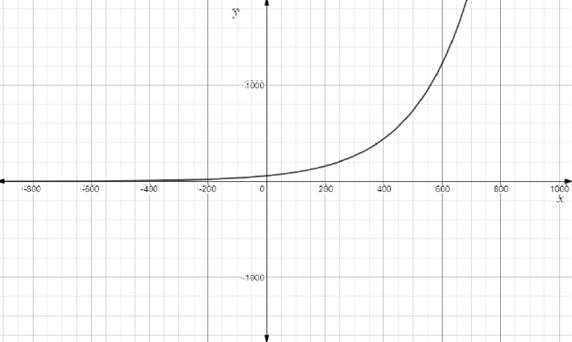EBK PRECALCULUS W/LIMITS, Chapter 3.1, Problem 62E By looking at the graph it is clear that the population of Italy increasing.

To determine

To find: the populations of Italy in 2003 and 2015.

Expert Solution

Answer to Problem 62E

Population of Italy in 2003 is nearly 58.5 million.

Population of Italy in 2015 is nearly 62.2 million.

Explanation of Solution

Given:

The population P (in millions) of Italy from 2003 through 2015 can be approximated by the model

P=57.59e0.0051t .................. (1)

Where t represents the year, with t=3 corresponding to 2003.

The population of Italy in 2003 is found by substituting t=3 in equation (1),

P(3)=57.59e0.0051(3)=57.59e0.0153≈58.5

Thus, population of Italy in 2003 is nearly 58.5 million.

The population of Italy in 2015 is found by substituting t=15 in equation (1),

P(15)=57.59e0.0051(15)=57.59e0.0765≈62.2

Thus, population of Italy in 2015 is nearly 62.2 million.

To determine

To find: the populations of Italy in 2020 and 2025.

Expert Solution

Answer to Problem 62E

Population of Italy in 2020 is nearly 63.8 million.

Population of Italy in 2025 is nearly 65.4 million.

Explanation of Solution

Given:

The population P (in millions) of Italy from 2003 through 2015 can be approximated by the model

P=57.59e0.0051t .................. (1)

Where t represents the year, with t=3 corresponding to 2003.

The population of Italy in 2020 is found by substituting t=20 in equation (1),

P(20)=57.59e0.0051(20)=57.59e0.102≈63.8

Thus, population of Italy in 2025 is nearly 63.8 million.

The population of Italy in 2025 is found by substituting t=25 in equation (1),

P(25)=57.59e0.0051(25)=57.59e0.1275≈65.4

Thus, population of Italy in 2025 is nearly 65.4 million.

Chapter 3.1, Problem 61E

Chapter 3.1, Problem 63E

Chapter 3 Solutions

EBK PRECALCULUS W/LIMITS

Ch. 3.1 - Prob. 1E Ch. 3.1 - Prob. 2E Ch. 3.1 - Prob. 3E Ch. 3.1 - Prob. 4E Ch. 3.1 - Prob. 5E Ch. 3.1 - Prob. 6E Ch. 3.1 - Prob. 7E Ch. 3.1 - Prob. 8E Ch. 3.1 - Prob. 9E Ch. 3.1 - Prob. 10E

Ch. 3.1 - Prob. 11E Ch. 3.1 - Prob. 12E Ch. 3.1 - Prob. 13E Ch. 3.1 - Prob. 14E Ch. 3.1 - Prob. 15E Ch. 3.1 - Prob. 16E Ch. 3.1 - Prob. 17E Ch. 3.1 - Prob. 18E Ch. 3.1 - Prob. 19E Ch. 3.1 - Prob. 20E Ch. 3.1 - Prob. 21E Ch. 3.1 - Prob. 22E Ch. 3.1 - Prob. 23E Ch. 3.1 - Prob. 24E Ch. 3.1 - Prob. 25E Ch. 3.1 - Prob. 26E Ch. 3.1 - Prob. 27E Ch. 3.1 - Prob. 28E Ch. 3.1 - Prob. 29E Ch. 3.1 - Prob. 30E Ch. 3.1 - Prob. 31E Ch. 3.1 - Prob. 32E Ch. 3.1 - Prob. 33E Ch. 3.1 - Prob. 34E Ch. 3.1 - Prob. 35E Ch. 3.1 - Prob. 36E Ch. 3.1 - Prob. 37E Ch. 3.1 - Prob. 38E Ch. 3.1 - Prob. 39E Ch. 3.1 - Prob. 40E Ch. 3.1 - Prob. 41E Ch. 3.1 - Prob. 42E Ch. 3.1 - Prob. 43E Ch. 3.1 - Prob. 44E Ch. 3.1 - Prob. 45E Ch. 3.1 - Prob. 46E Ch. 3.1 - Prob. 47E Ch. 3.1 - Prob. 48E Ch. 3.1 - Prob. 49E Ch. 3.1 - Prob. 50E Ch. 3.1 - Prob. 51E Ch. 3.1 - Prob. 52E Ch. 3.1 - Prob. 53E Ch. 3.1 - Prob. 54E Ch. 3.1 - Prob. 55E Ch. 3.1 - Prob. 56E Ch. 3.1 - Prob. 57E Ch. 3.1 - Prob. 58E Ch. 3.1 - Prob. 59E Ch. 3.1 - Prob. 60E Ch. 3.1 - Prob. 61E Ch. 3.1 - Prob. 62E Ch. 3.1 - Prob. 63E Ch. 3.1 - Prob. 64E Ch. 3.1 - Prob. 65E Ch. 3.1 - Prob. 66E Ch. 3.1 - Prob. 67E Ch. 3.1 - Prob. 68E Ch. 3.1 - Prob. 69E Ch. 3.1 - Prob. 70E Ch. 3.1 - Prob. 71E Ch. 3.1 - Prob. 72E Ch. 3.1 - Prob. 73E Ch. 3.1 - Prob. 74E Ch. 3.1 - Prob. 75E Ch. 3.1 - Prob. 76E Ch. 3.1 - Prob. 77E Ch. 3.1 - Prob. 78E Ch. 3.1 - Prob. 79E Ch. 3.1 - Prob. 80E Ch. 3.2 - Prob. 1E Ch. 3.2 - Prob. 2E Ch. 3.2 - Prob. 3E Ch. 3.2 - Prob. 4E Ch. 3.2 - Prob. 5E Ch. 3.2 - Prob. 6E Ch. 3.2 - Prob. 7E Ch. 3.2 - Prob. 8E Ch. 3.2 - Prob. 9E Ch. 3.2 - Prob. 10E Ch. 3.2 - Prob. 11E Ch. 3.2 - Prob. 12E Ch. 3.2 - Prob. 13E Ch. 3.2 - Prob. 14E Ch. 3.2 - Prob. 15E Ch. 3.2 - Prob. 16E Ch. 3.2 - Prob. 17E Ch. 3.2 - Prob. 18E Ch. 3.2 - Prob. 19E Ch. 3.2 - Prob. 20E Ch. 3.2 - Prob. 21E Ch. 3.2 - Prob. 22E Ch. 3.2 - Prob. 23E Ch. 3.2 - Prob. 24E Ch. 3.2 - Prob. 25E Ch. 3.2 - Prob. 26E Ch. 3.2 - Prob. 27E Ch. 3.2 - Prob. 28E Ch. 3.2 - Prob. 29E Ch. 3.2 - Prob. 30E Ch. 3.2 - Prob. 31E Ch. 3.2 - Prob. 32E Ch. 3.2 - Prob. 33E Ch. 3.2 - Prob. 34E Ch. 3.2 - Prob. 35E Ch. 3.2 - Prob. 36E Ch. 3.2 - Prob. 37E Ch. 3.2 - Prob. 38E Ch. 3.2 - Prob. 39E Ch. 3.2 - Prob. 40E Ch. 3.2 - Prob. 41E Ch. 3.2 - Prob. 42E Ch. 3.2 - Prob. 43E Ch. 3.2 - Prob. 44E Ch. 3.2 - Prob. 45E Ch. 3.2 - Prob. 46E Ch. 3.2 - Prob. 47E Ch. 3.2 - Prob. 48E Ch. 3.2 - Prob. 49E Ch. 3.2 - Prob. 50E Ch. 3.2 - Prob. 51E Ch. 3.2 - Prob. 52E Ch. 3.2 - Prob. 53E Ch. 3.2 - Prob. 54E Ch. 3.2 - Prob. 55E Ch. 3.2 - Prob. 56E Ch. 3.2 - Prob. 57E Ch. 3.2 - Prob. 58E Ch. 3.2 - Prob. 59E Ch. 3.2 - Prob. 60E Ch. 3.2 - Prob. 61E Ch. 3.2 - Prob. 62E Ch. 3.2 - Prob. 63E Ch. 3.2 - Prob. 64E Ch. 3.2 - Prob. 65E Ch. 3.2 - Prob. 66E Ch. 3.2 - Prob. 67E Ch. 3.2 - Prob. 68E Ch. 3.2 - Prob. 69E Ch. 3.2 - Prob. 70E Ch. 3.2 - Prob. 71E Ch. 3.2 - Prob. 72E Ch. 3.2 - Prob. 73E Ch. 3.2 - Prob. 74E Ch. 3.2 - Prob. 75E Ch. 3.2 - Prob. 76E Ch. 3.2 - Prob. 77E Ch. 3.2 - Prob. 78E Ch. 3.2 - Prob. 79E Ch. 3.2 - Prob. 80E Ch. 3.2 - Prob. 81E Ch. 3.2 - Prob. 82E Ch. 3.2 - Prob. 83E Ch. 3.2 - Prob. 84E Ch. 3.2 - Prob. 85E Ch. 3.2 - Prob. 86E Ch. 3.2 - Prob. 87E Ch. 3.2 - Prob. 88E Ch. 3.2 - Prob. 89E Ch. 3.2 - Prob. 90E Ch. 3.2 - Prob. 91E Ch. 3.2 - Prob. 92E Ch. 3.3 - Prob. 1E Ch. 3.3 - Prob. 2E Ch. 3.3 - Prob. 3E Ch. 3.3 - Prob. 4E Ch. 3.3 - Prob. 5E Ch. 3.3 - Prob. 6E Ch. 3.3 - Prob. 7E Ch. 3.3 - Prob. 8E Ch. 3.3 - Prob. 9E Ch. 3.3 - Prob. 10E Ch. 3.3 - Prob. 11E Ch. 3.3 - Prob. 12E Ch. 3.3 - Prob. 13E Ch. 3.3 - Prob. 14E Ch. 3.3 - Prob. 15E Ch. 3.3 - Prob. 16E Ch. 3.3 - Prob. 17E Ch. 3.3 - Prob. 18E Ch. 3.3 - Prob. 19E Ch. 3.3 - Prob. 20E Ch. 3.3 - Prob. 21E Ch. 3.3 - Prob. 22E Ch. 3.3 - Prob. 23E Ch. 3.3 - Prob. 24E Ch. 3.3 - Prob. 25E Ch. 3.3 - Prob. 26E Ch. 3.3 - Prob. 27E Ch. 3.3 - Prob. 28E Ch. 3.3 - Prob. 29E Ch. 3.3 - Prob. 30E Ch. 3.3 - Prob. 31E Ch. 3.3 - Prob. 32E Ch. 3.3 - Prob. 33E Ch. 3.3 - Prob. 34E Ch. 3.3 - Prob. 35E Ch. 3.3 - Prob. 36E Ch. 3.3 - Prob. 37E Ch. 3.3 - Prob. 38E Ch. 3.3 - Prob. 39E Ch. 3.3 - Prob. 40E Ch. 3.3 - Prob. 41E Ch. 3.3 - Prob. 42E Ch. 3.3 - Prob. 43E Ch. 3.3 - Prob. 44E Ch. 3.3 - Prob. 45E Ch. 3.3 - Prob. 46E Ch. 3.3 - Prob. 47E Ch. 3.3 - Prob. 48E Ch. 3.3 - Prob. 49E Ch. 3.3 - Prob. 50E Ch. 3.3 - Prob. 51E Ch. 3.3 - Prob. 52E Ch. 3.3 - Prob. 53E Ch. 3.3 - Prob. 54E Ch. 3.3 - Prob. 55E Ch. 3.3 - Prob. 56E Ch. 3.3 - Prob. 57E Ch. 3.3 - Prob. 58E Ch. 3.3 - Prob. 59E Ch. 3.3 - Prob. 60E Ch. 3.3 - Prob. 61E Ch. 3.3 - Prob. 62E Ch. 3.3 - Prob. 63E Ch. 3.3 - Prob. 64E Ch. 3.3 - Prob. 65E Ch. 3.3 - Prob. 66E Ch. 3.3 - Prob. 67E Ch. 3.3 - Prob. 68E Ch. 3.3 - Prob. 69E Ch. 3.3 - Prob. 70E Ch. 3.3 - Prob. 71E Ch. 3.3 - Prob. 72E Ch. 3.3 - Prob. 73E Ch. 3.3 - Prob. 74E Ch. 3.3 - Prob. 75E Ch. 3.3 - Prob. 76E Ch. 3.3 - Prob. 77E Ch. 3.3 - Prob. 78E Ch. 3.3 - Prob. 79E Ch. 3.3 - Prob. 80E Ch. 3.3 - Prob. 81E Ch. 3.3 - Prob. 82E Ch. 3.3 - Prob. 83E Ch. 3.3 - Prob. 84E Ch. 3.3 - Prob. 85E Ch. 3.3 - Prob. 86E Ch. 3.3 - Prob. 87E Ch. 3.3 - Prob. 88E Ch. 3.3 - Prob. 89E Ch. 3.3 - Prob. 90E Ch. 3.3 - Prob. 91E Ch. 3.3 - Prob. 92E Ch. 3.3 - Prob. 93E Ch. 3.3 - Prob. 94E Ch. 3.3 - Prob. 95E Ch. 3.3 - Prob. 96E Ch. 3.3 - Prob. 97E Ch. 3.3 - Prob. 98E Ch. 3.3 - Prob. 99E Ch. 3.3 - Prob. 100E Ch. 3.3 - Prob. 101E Ch. 3.3 - Prob. 102E Ch. 3.3 - Prob. 103E Ch. 3.3 - Prob. 104E Ch. 3.3 - Prob. 105E Ch. 3.4 - Prob. 1E Ch. 3.4 - Prob. 2E Ch. 3.4 - Prob. 3E Ch. 3.4 - Prob. 4E Ch. 3.4 - Prob. 5E Ch. 3.4 - Prob. 6E Ch. 3.4 - Prob. 7E Ch. 3.4 - Prob. 8E Ch. 3.4 - Prob. 9E Ch. 3.4 - Prob. 10E Ch. 3.4 - Prob. 11E Ch. 3.4 - Prob. 12E Ch. 3.4 - Prob. 13E Ch. 3.4 - Prob. 14E Ch. 3.4 - Prob. 15E Ch. 3.4 - Prob. 16E Ch. 3.4 - Prob. 17E Ch. 3.4 - Prob. 18E Ch. 3.4 - Prob. 19E Ch. 3.4 - Prob. 20E Ch. 3.4 - Prob. 21E Ch. 3.4 - Prob. 22E Ch. 3.4 - Prob. 23E Ch. 3.4 - Prob. 24E Ch. 3.4 - Prob. 25E Ch. 3.4 - Prob. 26E Ch. 3.4 - Prob. 27E Ch. 3.4 - Prob. 28E Ch. 3.4 - Prob. 29E Ch. 3.4 - Prob. 30E Ch. 3.4 - Prob. 31E Ch. 3.4 - Prob. 32E Ch. 3.4 - Prob. 33E Ch. 3.4 - Prob. 34E Ch. 3.4 - Prob. 35E Ch. 3.4 - Prob. 36E Ch. 3.4 - Prob. 37E Ch. 3.4 - Prob. 38E Ch. 3.4 - Prob. 39E Ch. 3.4 - Prob. 40E Ch. 3.4 - Prob. 41E Ch. 3.4 - Prob. 42E Ch. 3.4 - Prob. 43E Ch. 3.4 - Prob. 44E Ch. 3.4 - Prob. 45E Ch. 3.4 - Prob. 46E Ch. 3.4 - Prob. 47E Ch. 3.4 - Prob. 48E Ch. 3.4 - Prob. 49E Ch. 3.4 - Prob. 50E Ch. 3.4 - Prob. 51E Ch. 3.4 - Prob. 52E Ch. 3.4 - Prob. 53E Ch. 3.4 - Prob. 54E Ch. 3.4 - Prob. 55E Ch. 3.4 - Prob. 56E Ch. 3.4 - Prob. 57E Ch. 3.4 - Prob. 58E Ch. 3.4 - Prob. 59E Ch. 3.4 - Prob. 60E Ch. 3.4 - Prob. 61E Ch. 3.4 - Prob. 62E Ch. 3.4 - Prob. 63E Ch. 3.4 - Prob. 64E Ch. 3.4 - Prob. 65E Ch. 3.4 - Prob. 66E Ch. 3.4 - Prob. 67E Ch. 3.4 - Prob. 68E Ch. 3.4 - Prob. 69E Ch. 3.4 - Prob. 70E Ch. 3.4 - Prob. 71E Ch. 3.4 - Prob. 72E Ch. 3.4 - Prob. 73E Ch. 3.4 - Prob. 74E Ch. 3.4 - Prob. 75E Ch. 3.4 - Prob. 76E Ch. 3.4 - Prob. 77E Ch. 3.4 - Prob. 78E Ch. 3.4 - Prob. 79E Ch. 3.4 - Prob. 80E Ch. 3.4 - Prob. 81E Ch. 3.4 - Prob. 82E Ch. 3.4 - Prob. 83E Ch. 3.4 - Prob. 84E Ch. 3.4 - Prob. 85E Ch. 3.4 - Prob. 86E Ch. 3.4 - Prob. 87E Ch. 3.4 - Prob. 88E Ch. 3.4 - Prob. 89E Ch. 3.4 - Prob. 90E Ch. 3.4 - Prob. 91E Ch. 3.4 - Prob. 92E Ch. 3.4 - Prob. 93E Ch. 3.4 - Prob. 94E Ch. 3.4 - Prob. 95E Ch. 3.4 - Prob. 96E Ch. 3.4 - Prob. 97E Ch. 3.4 - Prob. 98E Ch. 3.5 - Prob. 1E Ch. 3.5 - Prob. 2E Ch. 3.5 - Prob. 3E Ch. 3.5 - Prob. 4E Ch. 3.5 - Prob. 5E Ch. 3.5 - Prob. 6E Ch. 3.5 - Prob. 7E Ch. 3.5 - Prob. 8E Ch. 3.5 - Prob. 9E Ch. 3.5 - Prob. 10E Ch. 3.5 - Prob. 11E Ch. 3.5 - Prob. 12E Ch. 3.5 - Prob. 13E Ch. 3.5 - Prob. 14E Ch. 3.5 - Prob. 15E Ch. 3.5 - Prob. 16E Ch. 3.5 - Prob. 17E Ch. 3.5 - Prob. 18E Ch. 3.5 - Prob. 19E Ch. 3.5 - Prob. 20E Ch. 3.5 - Prob. 21E Ch. 3.5 - Prob. 22E Ch. 3.5 - Prob. 23E Ch. 3.5 - Prob. 24E Ch. 3.5 - Prob. 25E Ch. 3.5 - Prob. 26E Ch. 3.5 - Prob. 27E Ch. 3.5 - Prob. 28E Ch. 3.5 - Prob. 29E Ch. 3.5 - Prob. 30E Ch. 3.5 - Prob. 31E Ch. 3.5 - Prob. 32E Ch. 3.5 - Prob. 33E Ch. 3.5 - Prob. 34E Ch. 3.5 - Prob. 35E Ch. 3.5 - Prob. 36E Ch. 3.5 - Prob. 37E Ch. 3.5 - Prob. 38E Ch. 3.5 - Prob. 39E Ch. 3.5 - Prob. 40E Ch. 3.5 - Prob. 41E Ch. 3.5 - Prob. 42E Ch. 3.5 - Prob. 43E Ch. 3.5 - Prob. 44E Ch. 3.5 - Prob. 45E Ch. 3.5 - Prob. 46E Ch. 3.5 - Prob. 47E Ch. 3.5 - Prob. 48E Ch. 3.5 - Prob. 49E Ch. 3.5 - Prob. 50E Ch. 3.5 - Prob. 51E Ch. 3.5 - Prob. 52E Ch. 3.5 - Prob. 53E Ch. 3.5 - Prob. 54E Ch. 3.5 - Prob. 55E Ch. 3.5 - Prob. 56E Ch. 3.5 - Prob. 57E Ch. 3.5 - Prob. 58E Ch. 3.5 - Prob. 59E Ch. 3.5 - Prob. 60E Ch. 3.5 - Prob. 61E Ch. 3.5 - Prob. 62E Ch. 3.5 - Prob. 63E Ch. 3.5 - Prob. 64E Ch. 3.5 - Prob. 65E Ch. 3.5 - Prob. 66E Ch. 3 - Prob. 1RE Ch. 3 - Prob. 2RE Ch. 3 - Prob. 3RE Ch. 3 - Prob. 4RE Ch. 3 - Prob. 5RE Ch. 3 - Prob. 6RE Ch. 3 - Prob. 7RE Ch. 3 - Prob. 8RE Ch. 3 - Prob. 9RE Ch. 3 - Prob. 10RE Ch. 3 - Prob. 11RE Ch. 3 - Prob. 12RE Ch. 3 - Prob. 13RE Ch. 3 - Prob. 14RE Ch. 3 - Prob. 15RE Ch. 3 - Prob. 16RE Ch. 3 - Prob. 17RE Ch. 3 - Prob. 18RE Ch. 3 - Prob. 19RE Ch. 3 - Prob. 20RE Ch. 3 - Prob. 21RE Ch. 3 - Prob. 22RE Ch. 3 - Prob. 23RE Ch. 3 - Prob. 24RE Ch. 3 - Prob. 25RE Ch. 3 - Prob. 26RE Ch. 3 - Prob. 27RE Ch. 3 - Prob. 28RE Ch. 3 - Prob. 29RE Ch. 3 - Prob. 30RE Ch. 3 - Prob. 31RE Ch. 3 - Prob. 32RE Ch. 3 - Prob. 33RE Ch. 3 - Prob. 34RE Ch. 3 - Prob. 35RE Ch. 3 - Prob. 36RE Ch. 3 - Prob. 37RE Ch. 3 - Prob. 38RE Ch. 3 - Prob. 39RE Ch. 3 - Prob. 40RE Ch. 3 - Prob. 41RE Ch. 3 - Prob. 42RE Ch. 3 - Prob. 43RE Ch. 3 - Prob. 44RE Ch. 3 - Prob. 45RE Ch. 3 - Prob. 46RE Ch. 3 - Prob. 47RE Ch. 3 - Prob. 48RE Ch. 3 - Prob. 49RE Ch. 3 - Prob. 50RE Ch. 3 - Prob. 51RE Ch. 3 - Prob. 52RE Ch. 3 - Prob. 53RE Ch. 3 - Prob. 54RE Ch. 3 - Prob. 55RE Ch. 3 - Prob. 56RE Ch. 3 - Prob. 57RE Ch. 3 - Prob. 58RE Ch. 3 - Prob. 59RE Ch. 3 - Prob. 60RE Ch. 3 - Prob. 61RE Ch. 3 - Prob. 62RE Ch. 3 - Prob. 63RE Ch. 3 - Prob. 64RE Ch. 3 - Prob. 65RE Ch. 3 - Prob. 66RE Ch. 3 - Prob. 67RE Ch. 3 - Prob. 68RE Ch. 3 - Prob. 69RE Ch. 3 - Prob. 70RE Ch. 3 - Prob. 71RE Ch. 3 - Prob. 72RE Ch. 3 - Prob. 73RE Ch. 3 - Prob. 74RE Ch. 3 - Prob. 75RE Ch. 3 - Prob. 76RE Ch. 3 - Prob. 77RE Ch. 3 - Prob. 78RE Ch. 3 - Prob. 79RE Ch. 3 - Prob. 80RE Ch. 3 - Prob. 81RE Ch. 3 - Prob. 82RE Ch. 3 - Prob. 83RE Ch. 3 - Prob. 84RE Ch. 3 - Prob. 85RE Ch. 3 - Prob. 86RE Ch. 3 - Prob. 87RE Ch. 3 - Prob. 88RE Ch. 3 - Prob. 89RE Ch. 3 - Prob. 90RE Ch. 3 - Prob. 91RE Ch. 3 - Prob. 92RE Ch. 3 - Prob. 93RE Ch. 3 - Prob. 94RE Ch. 3 - Prob. 95RE Ch. 3 - Prob. 96RE Ch. 3 - Prob. 97RE Ch. 3 - Prob. 98RE Ch. 3 - Prob. 99RE Ch. 3 - Prob. 100RE Ch. 3 - Prob. 101RE Ch. 3 - Prob. 102RE Ch. 3 - Prob. 103RE Ch. 3 - Prob. 104RE Ch. 3 - Prob. 105RE Ch. 3 - Prob. 106RE Ch. 3 - Prob. 107RE Ch. 3 - Prob. 108RE Ch. 3 - Prob. 109RE Ch. 3 - Prob. 110RE Ch. 3 - Prob. 111RE Ch. 3 - Prob. 112RE Ch. 3 - Prob. 113RE Ch. 3 - Prob. 114RE Ch. 3 - Prob. 115RE Ch. 3 - Prob. 116RE Ch. 3 - Prob. 117RE Ch. 3 - Prob. 118RE Ch. 3 - Prob. 1CT Ch. 3 - Prob. 2CT Ch. 3 - Prob. 3CT Ch. 3 - Prob. 4CT Ch. 3 - Prob. 5CT Ch. 3 - Prob. 6CT Ch. 3 - Prob. 7CT Ch. 3 - Prob. 8CT Ch. 3 - Prob. 9CT Ch. 3 - Prob. 10CT Ch. 3 - Prob. 11CT Ch. 3 - Prob. 12CT Ch. 3 - Prob. 13CT Ch. 3 - Prob. 14CT Ch. 3 - Prob. 15CT Ch. 3 - Prob. 16CT Ch. 3 - Prob. 17CT Ch. 3 - Prob. 18CT Ch. 3 - Prob. 19CT Ch. 3 - Prob. 20CT Ch. 3 - Prob. 21CT Ch. 3 - Prob. 22CT Ch. 3 - Prob. 23CT Ch. 3 - Prob. 24CT Ch. 3 - Prob. 25CT Ch. 3 - Prob. 26CT Ch. 3 - Prob. 27CT Ch. 3 - Prob. 28CT Ch. 3 - Prob. 29CT Ch. 3 - Prob. 1CLT Ch. 3 - Prob. 2CLT Ch. 3 - Prob. 3CLT Ch. 3 - Prob. 4CLT Ch. 3 - Prob. 5CLT Ch. 3 - Prob. 6CLT Ch. 3 - Prob. 7CLT Ch. 3 - Prob. 8CLT Ch. 3 - Prob. 9CLT Ch. 3 - Prob. 10CLT Ch. 3 - Prob. 11CLT Ch. 3 - Prob. 12CLT Ch. 3 - Prob. 13CLT Ch. 3 - Prob. 14CLT Ch. 3 - Prob. 15CLT Ch. 3 - Prob. 16CLT Ch. 3 - Prob. 17CLT Ch. 3 - Prob. 18CLT Ch. 3 - Prob. 19CLT Ch. 3 - Prob. 20CLT Ch. 3 - Prob. 21CLT Ch. 3 - Prob. 22CLT Ch. 3 - Prob. 23CLT Ch. 3 - Prob. 24CLT Ch. 3 - Prob. 25CLT Ch. 3 - Prob. 26CLT Ch. 3 - Prob. 27CLT Ch. 3 - Prob. 28CLT Ch. 3 - Prob. 29CLT Ch. 3 - Prob. 30CLT Ch. 3 - Prob. 31CLT Ch. 3 - Prob. 32CLT Ch. 3 - Prob. 33CLT Ch. 3 - Prob. 34CLT Ch. 3 - Prob. 35CLT Ch. 3 - Prob. 36CLT Ch. 3 - Prob. 37CLT Ch. 3 - Prob. 38CLT Ch. 3 - Prob. 39CLT Ch. 3 - Prob. 40CLT Ch. 3 - Prob. 41CLT Ch. 3 - Prob. 42CLT Ch. 3 - Prob. 43CLT Ch. 3 - Prob. 1PS Ch. 3 - Prob. 2PS Ch. 3 - Prob. 3PS Ch. 3 - Prob. 4PS Ch. 3 - Prob. 5PS Ch. 3 - Prob. 6PS Ch. 3 - Prob. 7PS Ch. 3 - Prob. 8PS Ch. 3 - Prob. 9PS Ch. 3 - Prob. 10PS Ch. 3 - Prob. 11PS Ch. 3 - Prob. 12PS Ch. 3 - Prob. 13PS Ch. 3 - Prob. 14PS Ch. 3 - Prob. 15PS Ch. 3 - Prob. 16PS Ch. 3 - Prob. 17PS Ch. 3 - Prob. 18PS Ch. 3 - Prob. 19PS Ch. 3 - Prob. 20PS Ch. 3 - Prob. 21PS Ch. 3 - Prob. 22PS Ch. 3 - Prob. 23PS Ch. 3 - Prob. 24PS Ch. 3 - Prob. 25PS Ch. 3 - Prob. 26PS

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.