Glencoe Algebra 2 Student Edition C2014
1st Edition
ISBN: 9780076639908
Author: McGraw-Hill Glencoe
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 3.3, Problem 7CYU
(a)
To determine
To write: the inequalities that represent the production time and deck finishing and quality control time.
(a)
Expert Solution
Answer to Problem 7CYU
The inequalities are
Explanation of Solution
Given Information:
The total number of worker hours per day available for the production =
The total number of hours available for finishing decks and quality control =
The table for the skateboard manufacturing time is as follows.
| Skateboard manufacturing Time | ||
| Board Type | Production Time | Deck finishing/Quality Control Time |
| Pro Boards |
hours |
hours |
| Speciality Boards |
hour |
hours |
Let
Let
According to constraints production time, write the inequality as follows.
The constraint on total production time=
According to deck finishing and quality control time, write the inequality as follows.
The constrain on total deck finishing time =
Also the non-negative constraints are
(b)
To determine
To draw: the graph showing the feasible region.
(b)
Expert Solution
Explanation of Solution
Given Information:
According to constraints , the inequality as follows.
The constraint on total production time is
The constraint on total deck finishing time is
Also the non-negative constraints are
Explanation for plotting the graph :
The graph of
To plot
The graph of
To plot
Plotting the Graph:
Plot the graph of the inequality
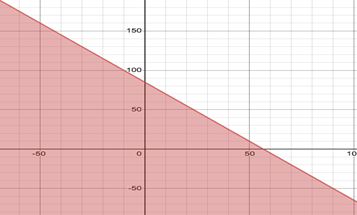
The graph of inequality
On the same graph plot the inequality
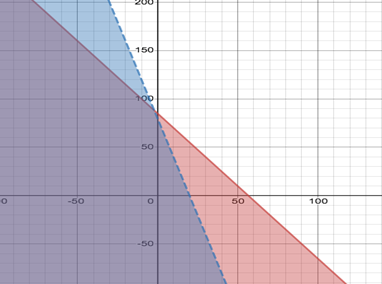
The graph of the inequality
Plot the non-negative constraints
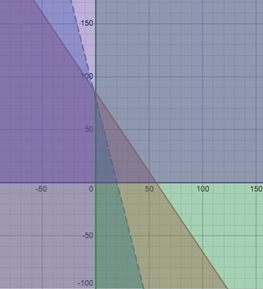
(c)
To determine
To list the coordinates of the vertices of the feasible region.
(c)
Expert Solution
Answer to Problem 7CYU
The coordinates of the vertices of the feasible region are
Explanation of Solution
Given Information:
The feasible region is given as follows
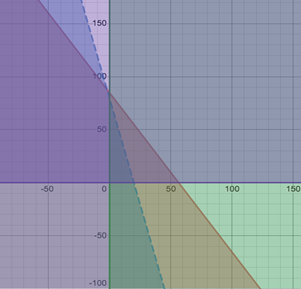
The graph of the feasible region
Mark the vertices of the feasible region and write its coordinates.
The graph showing the coordinates of the feasible region.
The coordinates of the vertices of the feasible region are
(d)
To determine
To write the function for the total profit on the skateboards.
(d)
Expert Solution
Answer to Problem 7CYU
Function
Explanation of Solution
Given Information:
The profit on one pro board =
The profit on specialty board =
Let
Let
The profit on
The profit on speciality board =
Therefore, function
(e)
To determine
To determine the number of each type of skateboards that need to made to have maximum profit. Also find the maximum profit.
(e)
Expert Solution
Answer to Problem 7CYU
The number of specialty skateboards =
The value of maximum profit =
Explanation of Solution
Given Information:
The profit function is given by
The coordinates of the vertices are
To maximise the profit function find the value at the vertices of the feasible region as follows.
| Vertices | Value of the profit function
|
|
|
|
|
|
|
|
|
|
The maximum value is
Result:
The number of specialty skateboards =
The value of maximum profit =
Chapter 3 Solutions
Glencoe Algebra 2 Student Edition C2014
Ch. 3.1 - Prob. 1ECh. 3.1 - Prob. 2ECh. 3.1 - Prob. 3ECh. 3.1 - Prob. 4ECh. 3.1 - Prob. 5ECh. 3.1 - Prob. 6ECh. 3.1 - Prob. 7ECh. 3.1 - Prob. 8ECh. 3.1 - Prob. 9ECh. 3.1 - Prob. 10E
Ch. 3.1 - Prob. 1AGPCh. 3.1 - Prob. 1BGPCh. 3.1 - Prob. 2AGPCh. 3.1 - Prob. 2BGPCh. 3.1 - Prob. 3AGPCh. 3.1 - Prob. 3BGPCh. 3.1 - Prob. 4AGPCh. 3.1 - Prob. 4BGPCh. 3.1 - Prob. 4CGPCh. 3.1 - Prob. 5AGPCh. 3.1 - Prob. 5BGPCh. 3.1 - Prob. 5CGPCh. 3.1 - Prob. 6GPCh. 3.1 - Prob. 1CYUCh. 3.1 - Prob. 2CYUCh. 3.1 - Prob. 3CYUCh. 3.1 - Prob. 4CYUCh. 3.1 - Prob. 5CYUCh. 3.1 - Prob. 6CYUCh. 3.1 - Prob. 7CYUCh. 3.1 - Prob. 8CYUCh. 3.1 - Prob. 9CYUCh. 3.1 - Prob. 10CYUCh. 3.1 - Prob. 11CYUCh. 3.1 - Prob. 12CYUCh. 3.1 - Prob. 13CYUCh. 3.1 - Prob. 14CYUCh. 3.1 - Prob. 15CYUCh. 3.1 - Prob. 16CYUCh. 3.1 - Prob. 17CYUCh. 3.1 - Prob. 18CYUCh. 3.1 - Prob. 19CYUCh. 3.1 - Prob. 20CYUCh. 3.1 - Prob. 21CYUCh. 3.1 - Prob. 22CYUCh. 3.1 - Prob. 23CYUCh. 3.1 - Prob. 24CYUCh. 3.1 - Prob. 25CYUCh. 3.1 - Prob. 26PPSCh. 3.1 - Prob. 27PPSCh. 3.1 - Prob. 28PPSCh. 3.1 - Prob. 29PPSCh. 3.1 - Prob. 30PPSCh. 3.1 - Prob. 31PPSCh. 3.1 - Prob. 32PPSCh. 3.1 - Prob. 33PPSCh. 3.1 - Prob. 34PPSCh. 3.1 - Prob. 35PPSCh. 3.1 - Prob. 36PPSCh. 3.1 - Prob. 37PPSCh. 3.1 - Prob. 38PPSCh. 3.1 - Prob. 39PPSCh. 3.1 - Prob. 40PPSCh. 3.1 - Prob. 41PPSCh. 3.1 - Prob. 42PPSCh. 3.1 - Prob. 43PPSCh. 3.1 - Prob. 44PPSCh. 3.1 - Prob. 45PPSCh. 3.1 - Prob. 46PPSCh. 3.1 - Prob. 47PPSCh. 3.1 - Prob. 48PPSCh. 3.1 - Prob. 49PPSCh. 3.1 - Prob. 50PPSCh. 3.1 - Prob. 51PPSCh. 3.1 - Prob. 52PPSCh. 3.1 - Prob. 53PPSCh. 3.1 - Prob. 54PPSCh. 3.1 - Prob. 55PPSCh. 3.1 - Prob. 56PPSCh. 3.1 - Prob. 57PPSCh. 3.1 - Prob. 58PPSCh. 3.1 - Prob. 59PPSCh. 3.1 - Prob. 60PPSCh. 3.1 - Prob. 61PPSCh. 3.1 - Prob. 62PPSCh. 3.1 - Prob. 63PPSCh. 3.1 - Prob. 64PPSCh. 3.1 - Prob. 65PPSCh. 3.1 - Prob. 66PPSCh. 3.1 - Prob. 67PPSCh. 3.1 - Prob. 68PPSCh. 3.1 - Prob. 69PPSCh. 3.1 - Prob. 70PPSCh. 3.1 - Prob. 71PPSCh. 3.1 - Prob. 72PPSCh. 3.1 - Prob. 73PPSCh. 3.1 - Prob. 74PPSCh. 3.1 - Prob. 75PPSCh. 3.1 - Prob. 76HPCh. 3.1 - Prob. 77HPCh. 3.1 - Prob. 78HPCh. 3.1 - Prob. 79HPCh. 3.1 - Prob. 80HPCh. 3.1 - Prob. 81STPCh. 3.1 - Prob. 82STPCh. 3.1 - Prob. 83STPCh. 3.1 - Prob. 84STPCh. 3.1 - Prob. 85SRCh. 3.1 - Prob. 86SRCh. 3.1 - Prob. 87SRCh. 3.1 - Prob. 88SRCh. 3.1 - Prob. 89SRCh. 3.1 - Prob. 90SRCh. 3.1 - Prob. 91SRCh. 3.1 - Prob. 92SRCh. 3.1 - Prob. 93SRCh. 3.1 - Prob. 94SRCh. 3.1 - Prob. 95SCh. 3.1 - Prob. 96SCh. 3.1 - Prob. 97SCh. 3.2 - Prob. 1AGPCh. 3.2 - Prob. 1BGPCh. 3.2 - Prob. 2AGPCh. 3.2 - Prob. 2BGPCh. 3.2 - Prob. 3GPCh. 3.2 - Prob. 4AGPCh. 3.2 - Prob. 4BGPCh. 3.2 - Prob. 1CYUCh. 3.2 - Prob. 2CYUCh. 3.2 - Prob. 3CYUCh. 3.2 - Prob. 4CYUCh. 3.2 - Prob. 5CYUCh. 3.2 - Prob. 6CYUCh. 3.2 - Prob. 7PPSCh. 3.2 - Prob. 8PPSCh. 3.2 - Prob. 9PPSCh. 3.2 - Prob. 10PPSCh. 3.2 - Prob. 11PPSCh. 3.2 - Prob. 12PPSCh. 3.2 - Prob. 13PPSCh. 3.2 - Prob. 14PPSCh. 3.2 - Prob. 15PPSCh. 3.2 - Prob. 16PPSCh. 3.2 - Prob. 17PPSCh. 3.2 - Prob. 18PPSCh. 3.2 - Prob. 19PPSCh. 3.2 - Prob. 20PPSCh. 3.2 - Prob. 21PPSCh. 3.2 - Prob. 22PPSCh. 3.2 - Prob. 23PPSCh. 3.2 - Prob. 24PPSCh. 3.2 - Prob. 25PPSCh. 3.2 - Prob. 26PPSCh. 3.2 - Prob. 27PPSCh. 3.2 - Prob. 28PPSCh. 3.2 - Prob. 29PPSCh. 3.2 - Prob. 30PPSCh. 3.2 - Prob. 31PPSCh. 3.2 - Prob. 32PPSCh. 3.2 - Prob. 33PPSCh. 3.2 - Prob. 34PPSCh. 3.2 - Prob. 35PPSCh. 3.2 - Prob. 36PPSCh. 3.2 - Prob. 37PPSCh. 3.2 - Prob. 38PPSCh. 3.2 - Prob. 39PPSCh. 3.2 - Prob. 40PPSCh. 3.2 - Prob. 41PPSCh. 3.2 - Prob. 42PPSCh. 3.2 - Prob. 43PPSCh. 3.2 - Prob. 44PPSCh. 3.2 - Prob. 45HPCh. 3.2 - Prob. 46HPCh. 3.2 - Prob. 47HPCh. 3.2 - Prob. 48HPCh. 3.2 - Prob. 49HPCh. 3.2 - Prob. 50HPCh. 3.2 - Prob. 51STPCh. 3.2 - Prob. 52STPCh. 3.2 - Prob. 53STPCh. 3.2 - Prob. 54STPCh. 3.2 - Prob. 55SRCh. 3.2 - Prob. 56SRCh. 3.2 - Prob. 57SRCh. 3.2 - Prob. 58SRCh. 3.2 - Prob. 59SRCh. 3.2 - Prob. 60SRCh. 3.2 - Prob. 61SRCh. 3.2 - Prob. 62SRCh. 3.2 - Prob. 63SCh. 3.2 - Prob. 64SCh. 3.2 - Prob. 65SCh. 3.2 - Prob. 66SCh. 3.2 - Prob. 67SCh. 3.2 - Prob. 68SCh. 3.3 - Prob. 1ECh. 3.3 - Prob. 2ECh. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Prob. 5ECh. 3.3 - Prob. 6ECh. 3.3 - Prob. 7ECh. 3.3 - Prob. 8ECh. 3.3 - Prob. 9ECh. 3.3 - Prob. 1AGPCh. 3.3 - Prob. 1BGPCh. 3.3 - Prob. 2AGPCh. 3.3 - Prob. 2BGPCh. 3.3 - Prob. 3GPCh. 3.3 - Prob. 1CYUCh. 3.3 - Prob. 2CYUCh. 3.3 - Prob. 3CYUCh. 3.3 - Prob. 4CYUCh. 3.3 - Prob. 5CYUCh. 3.3 - Prob. 6CYUCh. 3.3 - Prob. 7CYUCh. 3.3 - Prob. 8PPSCh. 3.3 - Prob. 9PPSCh. 3.3 - Prob. 10PPSCh. 3.3 - Prob. 11PPSCh. 3.3 - Prob. 12PPSCh. 3.3 - Prob. 13PPSCh. 3.3 - Prob. 14PPSCh. 3.3 - Prob. 15PPSCh. 3.3 - Prob. 16PPSCh. 3.3 - Prob. 17PPSCh. 3.3 - Prob. 18PPSCh. 3.3 - Prob. 19PPSCh. 3.3 - Prob. 20PPSCh. 3.3 - Prob. 21PPSCh. 3.3 - Prob. 22PPSCh. 3.3 - Prob. 23PPSCh. 3.3 - Prob. 24PPSCh. 3.3 - Prob. 25PPSCh. 3.3 - Prob. 26PPSCh. 3.3 - Prob. 27PPSCh. 3.3 - Prob. 28PPSCh. 3.3 - Prob. 29HPCh. 3.3 - Prob. 30HPCh. 3.3 - Prob. 31HPCh. 3.3 - Prob. 32HPCh. 3.3 - Prob. 33HPCh. 3.3 - Prob. 34STPCh. 3.3 - Prob. 35STPCh. 3.3 - Prob. 36STPCh. 3.3 - Prob. 37STPCh. 3.3 - Prob. 38SRCh. 3.3 - Prob. 39SRCh. 3.3 - Prob. 40SRCh. 3.3 - Prob. 41SRCh. 3.3 - Prob. 42SRCh. 3.3 - Prob. 43SRCh. 3.3 - Prob. 44SRCh. 3.3 - Prob. 45SRCh. 3.3 - Prob. 46SRCh. 3.3 - Prob. 47SRCh. 3.3 - Prob. 48SRCh. 3.3 - Prob. 49SRCh. 3.3 - Prob. 50SCh. 3.3 - Prob. 51SCh. 3.3 - Prob. 52SCh. 3.3 - Prob. 53SCh. 3.3 - Prob. 54SCh. 3.3 - Prob. 55SCh. 3.4 - Prob. 1AGPCh. 3.4 - Prob. 1BGPCh. 3.4 - Prob. 2AGPCh. 3.4 - Prob. 2BGPCh. 3.4 - Prob. 3GPCh. 3.4 - Prob. 1CYUCh. 3.4 - Prob. 2CYUCh. 3.4 - Prob. 3CYUCh. 3.4 - Prob. 4CYUCh. 3.4 - Prob. 5CYUCh. 3.4 - Prob. 6CYUCh. 3.4 - Prob. 7CYUCh. 3.4 - Prob. 8PPSCh. 3.4 - Prob. 9PPSCh. 3.4 - Prob. 10PPSCh. 3.4 - Prob. 11PPSCh. 3.4 - Prob. 12PPSCh. 3.4 - Prob. 13PPSCh. 3.4 - Prob. 14PPSCh. 3.4 - Prob. 15PPSCh. 3.4 - Prob. 16PPSCh. 3.4 - Prob. 17PPSCh. 3.4 - Prob. 18PPSCh. 3.4 - Prob. 19PPSCh. 3.4 - Prob. 20PPSCh. 3.4 - Prob. 21PPSCh. 3.4 - Prob. 22PPSCh. 3.4 - Prob. 23PPSCh. 3.4 - Prob. 24HPCh. 3.4 - Prob. 25HPCh. 3.4 - Prob. 26HPCh. 3.4 - Prob. 27HPCh. 3.4 - Prob. 28HPCh. 3.4 - Prob. 29HPCh. 3.4 - Prob. 30STPCh. 3.4 - Prob. 31STPCh. 3.4 - Prob. 32STPCh. 3.4 - Prob. 33STPCh. 3.4 - Prob. 34SRCh. 3.4 - Prob. 35SRCh. 3.4 - Prob. 36SRCh. 3.4 - Prob. 37SRCh. 3.4 - Prob. 38SRCh. 3.4 - Prob. 39SCh. 3.4 - Prob. 40SCh. 3.4 - Prob. 41SCh. 3.4 - Prob. 42SCh. 3.4 - Prob. 1ECh. 3.4 - Prob. 2ECh. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - Prob. 13ECh. 3.4 - Prob. 14ECh. 3.4 - Prob. 15ECh. 3.4 - Prob. 16ECh. 3.4 - Prob. 17ECh. 3.4 - Prob. 18ECh. 3.4 - Prob. 19ECh. 3.5 - Prob. 1ECh. 3.5 - Prob. 2ECh. 3.5 - Prob. 3ECh. 3.5 - Prob. 4ECh. 3.5 - Prob. 1GPCh. 3.5 - Prob. 2AGPCh. 3.5 - Prob. 2BGPCh. 3.5 - Prob. 2CGPCh. 3.5 - Prob. 3GPCh. 3.5 - Prob. 4GPCh. 3.5 - Prob. 5GPCh. 3.5 - Prob. 1CYUCh. 3.5 - Prob. 2CYUCh. 3.5 - Prob. 3CYUCh. 3.5 - Prob. 4CYUCh. 3.5 - Prob. 5CYUCh. 3.5 - Prob. 6CYUCh. 3.5 - Prob. 7CYUCh. 3.5 - Prob. 8CYUCh. 3.5 - Prob. 9CYUCh. 3.5 - Prob. 10CYUCh. 3.5 - Prob. 11CYUCh. 3.5 - Prob. 12CYUCh. 3.5 - Prob. 13PPSCh. 3.5 - Prob. 14PPSCh. 3.5 - Prob. 15PPSCh. 3.5 - Prob. 16PPSCh. 3.5 - Prob. 17PPSCh. 3.5 - Prob. 18PPSCh. 3.5 - Prob. 19PPSCh. 3.5 - Prob. 20PPSCh. 3.5 - Prob. 21PPSCh. 3.5 - Prob. 22PPSCh. 3.5 - Prob. 23PPSCh. 3.5 - Prob. 24PPSCh. 3.5 - Prob. 25PPSCh. 3.5 - Prob. 26PPSCh. 3.5 - Prob. 27PPSCh. 3.5 - Prob. 28PPSCh. 3.5 - Prob. 29PPSCh. 3.5 - Prob. 30PPSCh. 3.5 - Prob. 31HPCh. 3.5 - Prob. 32HPCh. 3.5 - Prob. 33HPCh. 3.5 - Prob. 34HPCh. 3.5 - Prob. 35HPCh. 3.5 - Prob. 36HPCh. 3.5 - Prob. 37STPCh. 3.5 - Prob. 38STPCh. 3.5 - Prob. 39STPCh. 3.5 - Prob. 40STPCh. 3.5 - Prob. 41SRCh. 3.5 - Prob. 42SRCh. 3.5 - Prob. 43SRCh. 3.5 - Prob. 44SRCh. 3.5 - Prob. 45SRCh. 3.5 - Prob. 46SRCh. 3.5 - Prob. 47SRCh. 3.5 - Prob. 48SRCh. 3.5 - Prob. 49SRCh. 3.5 - Prob. 50SCh. 3.5 - Prob. 51SCh. 3.5 - Prob. 52SCh. 3.6 - Prob. 1AGPCh. 3.6 - Prob. 1BGPCh. 3.6 - Prob. 2GPCh. 3.6 - Prob. 3GPCh. 3.6 - Prob. 4GPCh. 3.6 - Prob. 5GPCh. 3.6 - Prob. 1CYUCh. 3.6 - Prob. 2CYUCh. 3.6 - Prob. 3CYUCh. 3.6 - Prob. 4CYUCh. 3.6 - Prob. 5CYUCh. 3.6 - Prob. 6CYUCh. 3.6 - Prob. 7CYUCh. 3.6 - Prob. 8CYUCh. 3.6 - Prob. 9CYUCh. 3.6 - Prob. 10CYUCh. 3.6 - Prob. 11CYUCh. 3.6 - Prob. 12CYUCh. 3.6 - Prob. 13CYUCh. 3.6 - Prob. 14CYUCh. 3.6 - Prob. 15PPSCh. 3.6 - Prob. 16PPSCh. 3.6 - Prob. 17PPSCh. 3.6 - Prob. 18PPSCh. 3.6 - Prob. 19PPSCh. 3.6 - Prob. 20PPSCh. 3.6 - Prob. 21PPSCh. 3.6 - Prob. 22PPSCh. 3.6 - Prob. 23PPSCh. 3.6 - Prob. 24PPSCh. 3.6 - Prob. 25PPSCh. 3.6 - Prob. 26PPSCh. 3.6 - Prob. 27PPSCh. 3.6 - Prob. 28PPSCh. 3.6 - Prob. 29PPSCh. 3.6 - Prob. 30PPSCh. 3.6 - Prob. 31PPSCh. 3.6 - Prob. 32PPSCh. 3.6 - Prob. 33PPSCh. 3.6 - Prob. 34PPSCh. 3.6 - Prob. 35PPSCh. 3.6 - Prob. 36PPSCh. 3.6 - Prob. 37PPSCh. 3.6 - Prob. 38PPSCh. 3.6 - Prob. 39PPSCh. 3.6 - Prob. 40PPSCh. 3.6 - Prob. 41PPSCh. 3.6 - Prob. 42PPSCh. 3.6 - Prob. 43PPSCh. 3.6 - Prob. 44PPSCh. 3.6 - Prob. 45PPSCh. 3.6 - Prob. 46HPCh. 3.6 - Prob. 47HPCh. 3.6 - Prob. 48HPCh. 3.6 - Prob. 49HPCh. 3.6 - Prob. 50HPCh. 3.6 - Prob. 51STPCh. 3.6 - Prob. 52STPCh. 3.6 - Prob. 53STPCh. 3.6 - Prob. 54STPCh. 3.6 - Prob. 55SRCh. 3.6 - Prob. 56SRCh. 3.6 - Prob. 57SRCh. 3.6 - Prob. 58SRCh. 3.6 - Prob. 59SRCh. 3.6 - Prob. 60SRCh. 3.6 - Prob. 61SRCh. 3.6 - Prob. 62SRCh. 3.6 - Prob. 63SCh. 3.6 - Prob. 64SCh. 3.6 - Prob. 65SCh. 3.6 - Prob. 1ECh. 3.6 - Prob. 2ECh. 3.6 - Prob. 3ECh. 3.6 - Prob. 4ECh. 3.6 - Prob. 5ECh. 3.6 - Prob. 6ECh. 3.6 - Prob. 7ECh. 3.6 - Prob. 8ECh. 3.6 - Prob. 9ECh. 3.6 - Prob. 10ECh. 3.6 - Prob. 11ECh. 3.6 - Prob. 12ECh. 3.6 - Prob. 13ECh. 3.6 - Prob. 14ECh. 3.7 - Prob. 1AGPCh. 3.7 - Prob. 1BGPCh. 3.7 - Prob. 2AGPCh. 3.7 - Prob. 2BGPCh. 3.7 - Prob. 3GPCh. 3.7 - Prob. 4AGPCh. 3.7 - Prob. 4BGPCh. 3.7 - Prob. 5AGPCh. 3.7 - Prob. 5BGPCh. 3.7 - Prob. 1CYUCh. 3.7 - Prob. 2CYUCh. 3.7 - Prob. 3CYUCh. 3.7 - Prob. 4CYUCh. 3.7 - Prob. 5CYUCh. 3.7 - Prob. 6CYUCh. 3.7 - Prob. 7CYUCh. 3.7 - Prob. 8CYUCh. 3.7 - Prob. 9CYUCh. 3.7 - Prob. 10CYUCh. 3.7 - Prob. 11CYUCh. 3.7 - Prob. 12CYUCh. 3.7 - Prob. 13CYUCh. 3.7 - Prob. 14CYUCh. 3.7 - Prob. 15CYUCh. 3.7 - Prob. 16CYUCh. 3.7 - Prob. 17CYUCh. 3.7 - Prob. 18CYUCh. 3.7 - Prob. 19CYUCh. 3.7 - Prob. 20CYUCh. 3.7 - Prob. 21CYUCh. 3.7 - Prob. 22CYUCh. 3.7 - Prob. 23CYUCh. 3.7 - Prob. 24CYUCh. 3.7 - Prob. 25CYUCh. 3.7 - Prob. 26PPSCh. 3.7 - Prob. 27PPSCh. 3.7 - Prob. 28PPSCh. 3.7 - Prob. 29PPSCh. 3.7 - Prob. 30PPSCh. 3.7 - Prob. 31PPSCh. 3.7 - Prob. 32PPSCh. 3.7 - Prob. 33PPSCh. 3.7 - Prob. 34PPSCh. 3.7 - Prob. 35PPSCh. 3.7 - Prob. 36PPSCh. 3.7 - Prob. 37PPSCh. 3.7 - Prob. 38PPSCh. 3.7 - Prob. 39PPSCh. 3.7 - Prob. 40PPSCh. 3.7 - Prob. 41PPSCh. 3.7 - Prob. 42PPSCh. 3.7 - Prob. 43PPSCh. 3.7 - Prob. 44PPSCh. 3.7 - Prob. 45PPSCh. 3.7 - Prob. 46PPSCh. 3.7 - Prob. 47PPSCh. 3.7 - Prob. 48PPSCh. 3.7 - Prob. 49PPSCh. 3.7 - Prob. 50PPSCh. 3.7 - Prob. 51PPSCh. 3.7 - Prob. 52PPSCh. 3.7 - Prob. 53PPSCh. 3.7 - Prob. 54PPSCh. 3.7 - Prob. 55PPSCh. 3.7 - Prob. 56HPCh. 3.7 - Prob. 57HPCh. 3.7 - Prob. 58HPCh. 3.7 - Prob. 59HPCh. 3.7 - Prob. 60HPCh. 3.7 - Prob. 61HPCh. 3.7 - Prob. 62STPCh. 3.7 - Prob. 63STPCh. 3.7 - Prob. 64STPCh. 3.7 - Prob. 65STPCh. 3.7 - Prob. 66SRCh. 3.7 - Prob. 67SRCh. 3.7 - Prob. 68SRCh. 3.7 - Prob. 69SRCh. 3.7 - Prob. 70SRCh. 3.7 - Prob. 71SRCh. 3.7 - Prob. 72SRCh. 3.7 - Prob. 73SCh. 3.7 - Prob. 74SCh. 3.7 - Prob. 75SCh. 3.8 - Prob. 1GPCh. 3.8 - Prob. 2AGPCh. 3.8 - Prob. 2BGPCh. 3.8 - Prob. 3GPCh. 3.8 - Prob. 1CYUCh. 3.8 - Prob. 2CYUCh. 3.8 - Prob. 3CYUCh. 3.8 - Prob. 4CYUCh. 3.8 - Prob. 5CYUCh. 3.8 - Prob. 6CYUCh. 3.8 - Prob. 7CYUCh. 3.8 - Prob. 8CYUCh. 3.8 - Prob. 9CYUCh. 3.8 - Prob. 10CYUCh. 3.8 - Prob. 11CYUCh. 3.8 - Prob. 12CYUCh. 3.8 - Prob. 13PPSCh. 3.8 - Prob. 14PPSCh. 3.8 - Prob. 15PPSCh. 3.8 - Prob. 16PPSCh. 3.8 - Prob. 17PPSCh. 3.8 - Prob. 18PPSCh. 3.8 - Prob. 19PPSCh. 3.8 - Prob. 20PPSCh. 3.8 - Prob. 21PPSCh. 3.8 - Prob. 22PPSCh. 3.8 - Prob. 23PPSCh. 3.8 - Prob. 24PPSCh. 3.8 - Prob. 25PPSCh. 3.8 - Prob. 26PPSCh. 3.8 - Prob. 27PPSCh. 3.8 - Prob. 28PPSCh. 3.8 - Prob. 29PPSCh. 3.8 - Prob. 30PPSCh. 3.8 - Prob. 31PPSCh. 3.8 - Prob. 32PPSCh. 3.8 - Prob. 33PPSCh. 3.8 - Prob. 34PPSCh. 3.8 - Prob. 35PPSCh. 3.8 - Prob. 36PPSCh. 3.8 - Prob. 37PPSCh. 3.8 - Prob. 38HPCh. 3.8 - Prob. 39HPCh. 3.8 - Prob. 40HPCh. 3.8 - Prob. 41HPCh. 3.8 - Prob. 42HPCh. 3.8 - Prob. 43STPCh. 3.8 - Prob. 44STPCh. 3.8 - Prob. 45STPCh. 3.8 - Prob. 46STPCh. 3.8 - Prob. 47SRCh. 3.8 - Prob. 48SRCh. 3.8 - Prob. 49SRCh. 3.8 - Prob. 50SRCh. 3.8 - Prob. 51SRCh. 3.8 - Prob. 52SRCh. 3.8 - Prob. 53SRCh. 3.8 - Prob. 54SCh. 3.8 - Prob. 55SCh. 3.8 - Prob. 56SCh. 3.8 - Prob. 1ECh. 3.8 - Prob. 2ECh. 3.8 - Prob. 3ECh. 3.8 - Prob. 4ECh. 3.8 - Prob. 5ECh. 3.8 - Prob. 6ECh. 3 - Prob. 1QCCh. 3 - Prob. 2QCCh. 3 - Prob. 3QCCh. 3 - Prob. 4QCCh. 3 - Prob. 5QCCh. 3 - Prob. 6QCCh. 3 - Prob. 7QCCh. 3 - Prob. 8QCCh. 3 - Prob. 9QCCh. 3 - Prob. 10QCCh. 3 - Prob. 11QCCh. 3 - Prob. 12QCCh. 3 - Prob. 13QCCh. 3 - Prob. 14QCCh. 3 - Prob. 1SGRCh. 3 - Prob. 2SGRCh. 3 - Prob. 3SGRCh. 3 - Prob. 4SGRCh. 3 - Prob. 5SGRCh. 3 - Prob. 6SGRCh. 3 - Prob. 7SGRCh. 3 - Prob. 8SGRCh. 3 - Prob. 9SGRCh. 3 - Prob. 10SGRCh. 3 - Prob. 11SGRCh. 3 - Prob. 12SGRCh. 3 - Prob. 13SGRCh. 3 - Prob. 14SGRCh. 3 - Prob. 15SGRCh. 3 - Prob. 16SGRCh. 3 - Prob. 17SGRCh. 3 - Prob. 18SGRCh. 3 - Prob. 19SGRCh. 3 - Prob. 20SGRCh. 3 - Prob. 21SGRCh. 3 - Prob. 22SGRCh. 3 - Prob. 23SGRCh. 3 - Prob. 24SGRCh. 3 - Prob. 25SGRCh. 3 - Prob. 26SGRCh. 3 - Prob. 27SGRCh. 3 - Prob. 28SGRCh. 3 - Prob. 29SGRCh. 3 - Prob. 30SGRCh. 3 - Prob. 31SGRCh. 3 - Prob. 32SGRCh. 3 - Prob. 33SGRCh. 3 - Prob. 34SGRCh. 3 - Prob. 35SGRCh. 3 - Prob. 36SGRCh. 3 - Prob. 37SGRCh. 3 - Prob. 38SGRCh. 3 - Prob. 39SGRCh. 3 - Prob. 40SGRCh. 3 - Prob. 41SGRCh. 3 - Prob. 42SGRCh. 3 - Prob. 43SGRCh. 3 - Prob. 44SGRCh. 3 - Prob. 45SGRCh. 3 - Prob. 46SGRCh. 3 - Prob. 47SGRCh. 3 - Prob. 48SGRCh. 3 - Prob. 1PTCh. 3 - Prob. 2PTCh. 3 - Prob. 3PTCh. 3 - Prob. 4PTCh. 3 - Prob. 5PTCh. 3 - Prob. 6PTCh. 3 - Prob. 7PTCh. 3 - Prob. 8PTCh. 3 - Prob. 9PTCh. 3 - Prob. 10PTCh. 3 - Prob. 11PTCh. 3 - Prob. 12PTCh. 3 - Prob. 13PTCh. 3 - Prob. 14PTCh. 3 - Prob. 15PTCh. 3 - Prob. 16PTCh. 3 - Prob. 17PTCh. 3 - Prob. 18PTCh. 3 - Prob. 19PTCh. 3 - Prob. 20PTCh. 3 - Prob. 21PTCh. 3 - Prob. 22PTCh. 3 - Prob. 1ECh. 3 - Prob. 2ECh. 3 - Prob. 3ECh. 3 - Prob. 4ECh. 3 - Prob. 5ECh. 3 - Prob. 6ECh. 3 - Prob. 7ECh. 3 - Prob. 8ECh. 3 - Prob. 1STPCh. 3 - Prob. 2STPCh. 3 - Prob. 3STPCh. 3 - Prob. 4STPCh. 3 - Prob. 5STPCh. 3 - Prob. 6STPCh. 3 - Prob. 7STPCh. 3 - Prob. 8STPCh. 3 - Prob. 9STPCh. 3 - Prob. 10STPCh. 3 - Prob. 11STPCh. 3 - Prob. 12STPCh. 3 - Prob. 13STP
Additional Math Textbook Solutions
Find more solutions based on key concepts
Evaluate the integrals in Exercises 17–66.
23.
University Calculus: Early Transcendentals (4th Edition)
CHECK POINT I Let p and q represent the following statements: p : 3 + 5 = 8 q : 2 × 7 = 20. Determine the truth...
Thinking Mathematically (6th Edition)
Find the point-slope form of the line passing through the given points. Use the first point as (x1, .y1). Plot ...
College Algebra with Modeling & Visualization (5th Edition)
Other techniques Evaluate the following limits, where a and b are fixed real numbers. 39. limx1x21x1
Calculus: Early Transcendentals (2nd Edition)
Find how many SDs above the mean price would be predicted to cost.
Intro Stats, Books a la Carte Edition (5th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Find a polynomial with integer coefficients that satisfies the given conditions. T(x) has degree 4, zeros i and 1 + i, and constant term 12.arrow_forwardHow to solve 2542000/64132 without a calculator?arrow_forwardHow much is the circumference of a circle whose diameter is 7 feet?C =π darrow_forward
- How to solve 2542/64.132arrow_forwardAssume that you fancy polynomial splines, while you actually need ƒ(t) = e²/3 – 1 for t€ [−1, 1]. See the figure for a plot of f(t). Your goal is to approximate f(t) with an inter- polating polynomial spline of degree d that is given as sa(t) = • Σk=0 Pd,k bd,k(t) so that sd(tk) = = Pd,k for tk = −1 + 2 (given d > 0) with basis functions bd,k(t) = Σi±0 Cd,k,i = • The special case of d 0 is trivial: the only basis function b0,0 (t) is constant 1 and so(t) is thus constant po,0 for all t = [−1, 1]. ...9 The d+1 basis functions bd,k (t) form a ba- sis Bd {ba,o(t), ba,1(t), bd,d(t)} of the function space of all possible sα (t) functions. Clearly, you wish to find out, which of them given a particular maximal degree d is the best-possible approximation of f(t) in the least- squares sense. _ 1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 -0.1 -0.2 -0.3 -0.4 -0.5 -0.6 -0.7 -0.8 -0.9 -1 function f(t) = exp((2t)/3) - 1 to project -1 -0.9 -0.8 -0.7 -0.6 -0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5…arrow_forwardAn image processor considered a 750×750 pixels large subset of an image and converted it into gray-scale, resulting in matrix gIn - a false-color visualization of gIn is shown in the top-left below. He prepared a two-dim. box filter f1 as a 25×25 matrix with only the 5×5 values in the middle being non-zero – this filter is shown in the top-middle position below. He then convolved £1 with itself to get £2, before convolving £2 with itself to get f3. In both of the steps, he maintained the 25×25 size. Next, he convolved gIn with £3 to get gl. Which of the six panels below shows g1? Argue by explaining all the steps, so far: What did the image processor do when preparing ₤3? What image processing operation (from gin to g1) did he prepare and what's the effect that can be seen? Next, he convolved the rows of f3 with filter 1/2 (-1, 8, 0, -8, 1) to get f4 - you find a visualization of filter f 4 below. He then convolved gIn with f4 to get g2 and you can find the result shown below. What…arrow_forward
- 3ur Colors are enchanting and elusive. A multitude of color systems has been proposed over a three-digits number of years - maybe more than the number of purposes that they serve... - Everyone knows the additive RGB color system – we usually serve light-emitting IT components like monitors with colors in that system. Here, we use c = (r, g, b) RGB with r, g, bЄ [0,1] to describe a color c. = T For printing, however, we usually use the subtractive CMY color system. The same color c becomes c = (c, m, y) CMY (1-c, 1-m, 1-y) RGB Note how we use subscripts to indicate with coordinate system the coordinates correspond to. Explain, why it is not possible to find a linear transformation between RGB and CMY coordinates. Farbenlehr c von Goethe Erster Band. Roſt einen Defte mit fergen up Tübingen, is et 3. Cotta'fden Babarblung. ISIO Homogeneous coordinates give us a work-around: If we specify colors in 4D, instead, with the 4th coordinate being the homogeneous coordinate h so that every actual…arrow_forwardCan someone provide an answer & detailed explanation please? Thank you kindly!arrow_forwardGiven the cubic function f(x) = x^3-6x^2 + 11x- 6, do the following: Plot the graph of the function. Find the critical points and determine whether each is a local minimum, local maximum, or a saddle point. Find the inflection point(s) (if any).Identify the intervals where the function is increasing and decreasing. Determine the end behavior of the graph.arrow_forward
- Given the quadratic function f(x) = x^2-4x+3, plot the graph of the function and find the following: The vertex of the parabola .The x-intercepts (if any). The y-intercept. Create graph also before solve.arrow_forwardwhat model best fits this dataarrow_forwardRound as specified A) 257 down to the nearest 10’s place B) 650 to the nearest even hundreds, place C) 593 to the nearest 10’s place D) 4157 to the nearest hundreds, place E) 7126 to the nearest thousand place arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
Solve ANY Optimization Problem in 5 Steps w/ Examples. What are they and How do you solve them?; Author: Ace Tutors;https://www.youtube.com/watch?v=BfOSKc_sncg;License: Standard YouTube License, CC-BY
Types of solution in LPP|Basic|Multiple solution|Unbounded|Infeasible|GTU|Special case of LP problem; Author: Mechanical Engineering Management;https://www.youtube.com/watch?v=F-D2WICq8Sk;License: Standard YouTube License, CC-BY
Optimization Problems in Calculus; Author: Professor Dave Explains;https://www.youtube.com/watch?v=q1U6AmIa_uQ;License: Standard YouTube License, CC-BY
Introduction to Optimization; Author: Math with Dr. Claire;https://www.youtube.com/watch?v=YLzgYm2tN8E;License: Standard YouTube License, CC-BY