Glencoe Algebra 2 Student Edition C2014
Glencoe Algebra 2 Student Edition C2014
1st Edition
ISBN: 9780076639908
Author: McGraw-Hill Glencoe
Publisher: MCG
bartleby

Concept explainers

Family of Curves
A family of curves is a group of curves that are each described by a parametrization in which one or more variables are parameters. In general, the parameters have more complexity on the assembly of the curve than an ordinary linear transformation. These…
XZ Plane
In order to understand XZ plane, it's helpful to understand two-dimensional and three-dimensional spaces. To plot a point on a plane, two numbers are needed, and these two numbers in the plane can be represented as an ordered pair (a,b) where a and b are…
Euclidean Geometry
Geometry is the branch of mathematics that deals with flat surfaces like lines, angles, points, two-dimensional figures, etc. In Euclidean geometry, one studies the geometrical shapes that rely on different theorems and axioms. This (pure mathematics) ge…
Lines and Angles
In a two-dimensional plane, a line is simply a figure that joins two points. Usually, lines are used for presenting objects that are straight in shape and have minimal depth or width.
bartleby

Videos

Question
Book Icon
Chapter 3, Problem 7QC

a.

To determine

To write: An equation to model the sales of tickets

a.

Expert Solution
Check Mark

Answer to Problem 7QC

The equation to model the sales of tickets is 8.5a+5.25b=650

Explanation of Solution

Given Information:

A museum chargestickets at the rate of $8.50 for adults and $5.25 for children. It made a sum of $650 on a particular day.

Method Used:

The following approach is used to obtain the desired equation

(1) Assuming two variables corresponding to number of tickets issued to adults and children

(2) Expressing the total cost of tickets in terms of the tickets issued to adults and children

Calculation

Let the number of tickets issued to adults be denoted as a and that to children be b .

For the given cost per ticket for adult $8.50, the total cost of tickets issued to adults is 8. 50a . Similarly for the children, the total cost of tickets is 5.25b. Now, the total sum made out of ticket sales is $650. Thus, the total sum can be expressed in terms of the individual amounts as,

  8.5a+5.25b=650 ............. (1)

This gives the equation for the given set of conditions.

b.

To determine

To graph: The equation representing the ticket sales in the museum on a day.

b.

Expert Solution
Check Mark

Explanation of Solution

Given Information:

The equation of the ticket sales during a day in the museum as obtained in part a. is 8.5a+5.25b=650

Graph

The equation can be rearranged as follows.

  5.25b=650−8.5ab=650−8.5a5.25=123.8−1.619a=−1.619a+123.8

Now, this is of the form of equation of straight line y=mx+c

The graph can be obtained as follows.

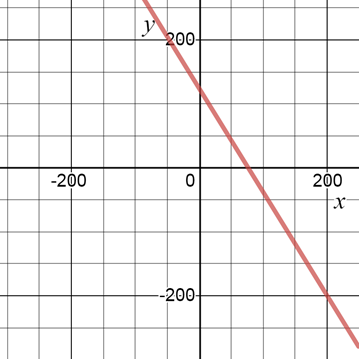
  Glencoe Algebra 2 Student Edition C2014, Chapter 3, Problem 7QC

Interpretation

The graph of the equation for sales of tickets is the form of a straight line. This shows that the variation of sales is in a linear fashion.

Previous
Chapter 3, Problem 6QC
Next
Chapter 3, Problem 8QC

Chapter 3 Solutions

Glencoe Algebra 2 Student Edition C2014

Ch. 3.1 - Prob. 1ECh. 3.1 - Prob. 2ECh. 3.1 - Prob. 3ECh. 3.1 - Prob. 4ECh. 3.1 - Prob. 5ECh. 3.1 - Prob. 6ECh. 3.1 - Prob. 7ECh. 3.1 - Prob. 8ECh. 3.1 - Prob. 9ECh. 3.1 - Prob. 10E
Ch. 3.1 - Prob. 1AGPCh. 3.1 - Prob. 1BGPCh. 3.1 - Prob. 2AGPCh. 3.1 - Prob. 2BGPCh. 3.1 - Prob. 3AGPCh. 3.1 - Prob. 3BGPCh. 3.1 - Prob. 4AGPCh. 3.1 - Prob. 4BGPCh. 3.1 - Prob. 4CGPCh. 3.1 - Prob. 5AGPCh. 3.1 - Prob. 5BGPCh. 3.1 - Prob. 5CGPCh. 3.1 - Prob. 6GPCh. 3.1 - Prob. 1CYUCh. 3.1 - Prob. 2CYUCh. 3.1 - Prob. 3CYUCh. 3.1 - Prob. 4CYUCh. 3.1 - Prob. 5CYUCh. 3.1 - Prob. 6CYUCh. 3.1 - Prob. 7CYUCh. 3.1 - Prob. 8CYUCh. 3.1 - Prob. 9CYUCh. 3.1 - Prob. 10CYUCh. 3.1 - Prob. 11CYUCh. 3.1 - Prob. 12CYUCh. 3.1 - Prob. 13CYUCh. 3.1 - Prob. 14CYUCh. 3.1 - Prob. 15CYUCh. 3.1 - Prob. 16CYUCh. 3.1 - Prob. 17CYUCh. 3.1 - Prob. 18CYUCh. 3.1 - Prob. 19CYUCh. 3.1 - Prob. 20CYUCh. 3.1 - Prob. 21CYUCh. 3.1 - Prob. 22CYUCh. 3.1 - Prob. 23CYUCh. 3.1 - Prob. 24CYUCh. 3.1 - Prob. 25CYUCh. 3.1 - Prob. 26PPSCh. 3.1 - Prob. 27PPSCh. 3.1 - Prob. 28PPSCh. 3.1 - Prob. 29PPSCh. 3.1 - Prob. 30PPSCh. 3.1 - Prob. 31PPSCh. 3.1 - Prob. 32PPSCh. 3.1 - Prob. 33PPSCh. 3.1 - Prob. 34PPSCh. 3.1 - Prob. 35PPSCh. 3.1 - Prob. 36PPSCh. 3.1 - Prob. 37PPSCh. 3.1 - Prob. 38PPSCh. 3.1 - Prob. 39PPSCh. 3.1 - Prob. 40PPSCh. 3.1 - Prob. 41PPSCh. 3.1 - Prob. 42PPSCh. 3.1 - Prob. 43PPSCh. 3.1 - Prob. 44PPSCh. 3.1 - Prob. 45PPSCh. 3.1 - Prob. 46PPSCh. 3.1 - Prob. 47PPSCh. 3.1 - Prob. 48PPSCh. 3.1 - Prob. 49PPSCh. 3.1 - Prob. 50PPSCh. 3.1 - Prob. 51PPSCh. 3.1 - Prob. 52PPSCh. 3.1 - Prob. 53PPSCh. 3.1 - Prob. 54PPSCh. 3.1 - Prob. 55PPSCh. 3.1 - Prob. 56PPSCh. 3.1 - Prob. 57PPSCh. 3.1 - Prob. 58PPSCh. 3.1 - Prob. 59PPSCh. 3.1 - Prob. 60PPSCh. 3.1 - Prob. 61PPSCh. 3.1 - Prob. 62PPSCh. 3.1 - Prob. 63PPSCh. 3.1 - Prob. 64PPSCh. 3.1 - Prob. 65PPSCh. 3.1 - Prob. 66PPSCh. 3.1 - Prob. 67PPSCh. 3.1 - Prob. 68PPSCh. 3.1 - Prob. 69PPSCh. 3.1 - Prob. 70PPSCh. 3.1 - Prob. 71PPSCh. 3.1 - Prob. 72PPSCh. 3.1 - Prob. 73PPSCh. 3.1 - Prob. 74PPSCh. 3.1 - Prob. 75PPSCh. 3.1 - Prob. 76HPCh. 3.1 - Prob. 77HPCh. 3.1 - Prob. 78HPCh. 3.1 - Prob. 79HPCh. 3.1 - Prob. 80HPCh. 3.1 - Prob. 81STPCh. 3.1 - Prob. 82STPCh. 3.1 - Prob. 83STPCh. 3.1 - Prob. 84STPCh. 3.1 - Prob. 85SRCh. 3.1 - Prob. 86SRCh. 3.1 - Prob. 87SRCh. 3.1 - Prob. 88SRCh. 3.1 - Prob. 89SRCh. 3.1 - Prob. 90SRCh. 3.1 - Prob. 91SRCh. 3.1 - Prob. 92SRCh. 3.1 - Prob. 93SRCh. 3.1 - Prob. 94SRCh. 3.1 - Prob. 95SCh. 3.1 - Prob. 96SCh. 3.1 - Prob. 97SCh. 3.2 - Prob. 1AGPCh. 3.2 - Prob. 1BGPCh. 3.2 - Prob. 2AGPCh. 3.2 - Prob. 2BGPCh. 3.2 - Prob. 3GPCh. 3.2 - Prob. 4AGPCh. 3.2 - Prob. 4BGPCh. 3.2 - Prob. 1CYUCh. 3.2 - Prob. 2CYUCh. 3.2 - Prob. 3CYUCh. 3.2 - Prob. 4CYUCh. 3.2 - Prob. 5CYUCh. 3.2 - Prob. 6CYUCh. 3.2 - Prob. 7PPSCh. 3.2 - Prob. 8PPSCh. 3.2 - Prob. 9PPSCh. 3.2 - Prob. 10PPSCh. 3.2 - Prob. 11PPSCh. 3.2 - Prob. 12PPSCh. 3.2 - Prob. 13PPSCh. 3.2 - Prob. 14PPSCh. 3.2 - Prob. 15PPSCh. 3.2 - Prob. 16PPSCh. 3.2 - Prob. 17PPSCh. 3.2 - Prob. 18PPSCh. 3.2 - Prob. 19PPSCh. 3.2 - Prob. 20PPSCh. 3.2 - Prob. 21PPSCh. 3.2 - Prob. 22PPSCh. 3.2 - Prob. 23PPSCh. 3.2 - Prob. 24PPSCh. 3.2 - Prob. 25PPSCh. 3.2 - Prob. 26PPSCh. 3.2 - Prob. 27PPSCh. 3.2 - Prob. 28PPSCh. 3.2 - Prob. 29PPSCh. 3.2 - Prob. 30PPSCh. 3.2 - Prob. 31PPSCh. 3.2 - Prob. 32PPSCh. 3.2 - Prob. 33PPSCh. 3.2 - Prob. 34PPSCh. 3.2 - Prob. 35PPSCh. 3.2 - Prob. 36PPSCh. 3.2 - Prob. 37PPSCh. 3.2 - Prob. 38PPSCh. 3.2 - Prob. 39PPSCh. 3.2 - Prob. 40PPSCh. 3.2 - Prob. 41PPSCh. 3.2 - Prob. 42PPSCh. 3.2 - Prob. 43PPSCh. 3.2 - Prob. 44PPSCh. 3.2 - Prob. 45HPCh. 3.2 - Prob. 46HPCh. 3.2 - Prob. 47HPCh. 3.2 - Prob. 48HPCh. 3.2 - Prob. 49HPCh. 3.2 - Prob. 50HPCh. 3.2 - Prob. 51STPCh. 3.2 - Prob. 52STPCh. 3.2 - Prob. 53STPCh. 3.2 - Prob. 54STPCh. 3.2 - Prob. 55SRCh. 3.2 - Prob. 56SRCh. 3.2 - Prob. 57SRCh. 3.2 - Prob. 58SRCh. 3.2 - Prob. 59SRCh. 3.2 - Prob. 60SRCh. 3.2 - Prob. 61SRCh. 3.2 - Prob. 62SRCh. 3.2 - Prob. 63SCh. 3.2 - Prob. 64SCh. 3.2 - Prob. 65SCh. 3.2 - Prob. 66SCh. 3.2 - Prob. 67SCh. 3.2 - Prob. 68SCh. 3.3 - Prob. 1ECh. 3.3 - Prob. 2ECh. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Prob. 5ECh. 3.3 - Prob. 6ECh. 3.3 - Prob. 7ECh. 3.3 - Prob. 8ECh. 3.3 - Prob. 9ECh. 3.3 - Prob. 1AGPCh. 3.3 - Prob. 1BGPCh. 3.3 - Prob. 2AGPCh. 3.3 - Prob. 2BGPCh. 3.3 - Prob. 3GPCh. 3.3 - Prob. 1CYUCh. 3.3 - Prob. 2CYUCh. 3.3 - Prob. 3CYUCh. 3.3 - Prob. 4CYUCh. 3.3 - Prob. 5CYUCh. 3.3 - Prob. 6CYUCh. 3.3 - Prob. 7CYUCh. 3.3 - Prob. 8PPSCh. 3.3 - Prob. 9PPSCh. 3.3 - Prob. 10PPSCh. 3.3 - Prob. 11PPSCh. 3.3 - Prob. 12PPSCh. 3.3 - Prob. 13PPSCh. 3.3 - Prob. 14PPSCh. 3.3 - Prob. 15PPSCh. 3.3 - Prob. 16PPSCh. 3.3 - Prob. 17PPSCh. 3.3 - Prob. 18PPSCh. 3.3 - Prob. 19PPSCh. 3.3 - Prob. 20PPSCh. 3.3 - Prob. 21PPSCh. 3.3 - Prob. 22PPSCh. 3.3 - Prob. 23PPSCh. 3.3 - Prob. 24PPSCh. 3.3 - Prob. 25PPSCh. 3.3 - Prob. 26PPSCh. 3.3 - Prob. 27PPSCh. 3.3 - Prob. 28PPSCh. 3.3 - Prob. 29HPCh. 3.3 - Prob. 30HPCh. 3.3 - Prob. 31HPCh. 3.3 - Prob. 32HPCh. 3.3 - Prob. 33HPCh. 3.3 - Prob. 34STPCh. 3.3 - Prob. 35STPCh. 3.3 - Prob. 36STPCh. 3.3 - Prob. 37STPCh. 3.3 - Prob. 38SRCh. 3.3 - Prob. 39SRCh. 3.3 - Prob. 40SRCh. 3.3 - Prob. 41SRCh. 3.3 - Prob. 42SRCh. 3.3 - Prob. 43SRCh. 3.3 - Prob. 44SRCh. 3.3 - Prob. 45SRCh. 3.3 - Prob. 46SRCh. 3.3 - Prob. 47SRCh. 3.3 - Prob. 48SRCh. 3.3 - Prob. 49SRCh. 3.3 - Prob. 50SCh. 3.3 - Prob. 51SCh. 3.3 - Prob. 52SCh. 3.3 - Prob. 53SCh. 3.3 - Prob. 54SCh. 3.3 - Prob. 55SCh. 3.4 - Prob. 1AGPCh. 3.4 - Prob. 1BGPCh. 3.4 - Prob. 2AGPCh. 3.4 - Prob. 2BGPCh. 3.4 - Prob. 3GPCh. 3.4 - Prob. 1CYUCh. 3.4 - Prob. 2CYUCh. 3.4 - Prob. 3CYUCh. 3.4 - Prob. 4CYUCh. 3.4 - Prob. 5CYUCh. 3.4 - Prob. 6CYUCh. 3.4 - Prob. 7CYUCh. 3.4 - Prob. 8PPSCh. 3.4 - Prob. 9PPSCh. 3.4 - Prob. 10PPSCh. 3.4 - Prob. 11PPSCh. 3.4 - Prob. 12PPSCh. 3.4 - Prob. 13PPSCh. 3.4 - Prob. 14PPSCh. 3.4 - Prob. 15PPSCh. 3.4 - Prob. 16PPSCh. 3.4 - Prob. 17PPSCh. 3.4 - Prob. 18PPSCh. 3.4 - Prob. 19PPSCh. 3.4 - Prob. 20PPSCh. 3.4 - Prob. 21PPSCh. 3.4 - Prob. 22PPSCh. 3.4 - Prob. 23PPSCh. 3.4 - Prob. 24HPCh. 3.4 - Prob. 25HPCh. 3.4 - Prob. 26HPCh. 3.4 - Prob. 27HPCh. 3.4 - Prob. 28HPCh. 3.4 - Prob. 29HPCh. 3.4 - Prob. 30STPCh. 3.4 - Prob. 31STPCh. 3.4 - Prob. 32STPCh. 3.4 - Prob. 33STPCh. 3.4 - Prob. 34SRCh. 3.4 - Prob. 35SRCh. 3.4 - Prob. 36SRCh. 3.4 - Prob. 37SRCh. 3.4 - Prob. 38SRCh. 3.4 - Prob. 39SCh. 3.4 - Prob. 40SCh. 3.4 - Prob. 41SCh. 3.4 - Prob. 42SCh. 3.4 - Prob. 1ECh. 3.4 - Prob. 2ECh. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - Prob. 13ECh. 3.4 - Prob. 14ECh. 3.4 - Prob. 15ECh. 3.4 - Prob. 16ECh. 3.4 - Prob. 17ECh. 3.4 - Prob. 18ECh. 3.4 - Prob. 19ECh. 3.5 - Prob. 1ECh. 3.5 - Prob. 2ECh. 3.5 - Prob. 3ECh. 3.5 - Prob. 4ECh. 3.5 - Prob. 1GPCh. 3.5 - Prob. 2AGPCh. 3.5 - Prob. 2BGPCh. 3.5 - Prob. 2CGPCh. 3.5 - Prob. 3GPCh. 3.5 - Prob. 4GPCh. 3.5 - Prob. 5GPCh. 3.5 - Prob. 1CYUCh. 3.5 - Prob. 2CYUCh. 3.5 - Prob. 3CYUCh. 3.5 - Prob. 4CYUCh. 3.5 - Prob. 5CYUCh. 3.5 - Prob. 6CYUCh. 3.5 - Prob. 7CYUCh. 3.5 - Prob. 8CYUCh. 3.5 - Prob. 9CYUCh. 3.5 - Prob. 10CYUCh. 3.5 - Prob. 11CYUCh. 3.5 - Prob. 12CYUCh. 3.5 - Prob. 13PPSCh. 3.5 - Prob. 14PPSCh. 3.5 - Prob. 15PPSCh. 3.5 - Prob. 16PPSCh. 3.5 - Prob. 17PPSCh. 3.5 - Prob. 18PPSCh. 3.5 - Prob. 19PPSCh. 3.5 - Prob. 20PPSCh. 3.5 - Prob. 21PPSCh. 3.5 - Prob. 22PPSCh. 3.5 - Prob. 23PPSCh. 3.5 - Prob. 24PPSCh. 3.5 - Prob. 25PPSCh. 3.5 - Prob. 26PPSCh. 3.5 - Prob. 27PPSCh. 3.5 - Prob. 28PPSCh. 3.5 - Prob. 29PPSCh. 3.5 - Prob. 30PPSCh. 3.5 - Prob. 31HPCh. 3.5 - Prob. 32HPCh. 3.5 - Prob. 33HPCh. 3.5 - Prob. 34HPCh. 3.5 - Prob. 35HPCh. 3.5 - Prob. 36HPCh. 3.5 - Prob. 37STPCh. 3.5 - Prob. 38STPCh. 3.5 - Prob. 39STPCh. 3.5 - Prob. 40STPCh. 3.5 - Prob. 41SRCh. 3.5 - Prob. 42SRCh. 3.5 - Prob. 43SRCh. 3.5 - Prob. 44SRCh. 3.5 - Prob. 45SRCh. 3.5 - Prob. 46SRCh. 3.5 - Prob. 47SRCh. 3.5 - Prob. 48SRCh. 3.5 - Prob. 49SRCh. 3.5 - Prob. 50SCh. 3.5 - Prob. 51SCh. 3.5 - Prob. 52SCh. 3.6 - Prob. 1AGPCh. 3.6 - Prob. 1BGPCh. 3.6 - Prob. 2GPCh. 3.6 - Prob. 3GPCh. 3.6 - Prob. 4GPCh. 3.6 - Prob. 5GPCh. 3.6 - Prob. 1CYUCh. 3.6 - Prob. 2CYUCh. 3.6 - Prob. 3CYUCh. 3.6 - Prob. 4CYUCh. 3.6 - Prob. 5CYUCh. 3.6 - Prob. 6CYUCh. 3.6 - Prob. 7CYUCh. 3.6 - Prob. 8CYUCh. 3.6 - Prob. 9CYUCh. 3.6 - Prob. 10CYUCh. 3.6 - Prob. 11CYUCh. 3.6 - Prob. 12CYUCh. 3.6 - Prob. 13CYUCh. 3.6 - Prob. 14CYUCh. 3.6 - Prob. 15PPSCh. 3.6 - Prob. 16PPSCh. 3.6 - Prob. 17PPSCh. 3.6 - Prob. 18PPSCh. 3.6 - Prob. 19PPSCh. 3.6 - Prob. 20PPSCh. 3.6 - Prob. 21PPSCh. 3.6 - Prob. 22PPSCh. 3.6 - Prob. 23PPSCh. 3.6 - Prob. 24PPSCh. 3.6 - Prob. 25PPSCh. 3.6 - Prob. 26PPSCh. 3.6 - Prob. 27PPSCh. 3.6 - Prob. 28PPSCh. 3.6 - Prob. 29PPSCh. 3.6 - Prob. 30PPSCh. 3.6 - Prob. 31PPSCh. 3.6 - Prob. 32PPSCh. 3.6 - Prob. 33PPSCh. 3.6 - Prob. 34PPSCh. 3.6 - Prob. 35PPSCh. 3.6 - Prob. 36PPSCh. 3.6 - Prob. 37PPSCh. 3.6 - Prob. 38PPSCh. 3.6 - Prob. 39PPSCh. 3.6 - Prob. 40PPSCh. 3.6 - Prob. 41PPSCh. 3.6 - Prob. 42PPSCh. 3.6 - Prob. 43PPSCh. 3.6 - Prob. 44PPSCh. 3.6 - Prob. 45PPSCh. 3.6 - Prob. 46HPCh. 3.6 - Prob. 47HPCh. 3.6 - Prob. 48HPCh. 3.6 - Prob. 49HPCh. 3.6 - Prob. 50HPCh. 3.6 - Prob. 51STPCh. 3.6 - Prob. 52STPCh. 3.6 - Prob. 53STPCh. 3.6 - Prob. 54STPCh. 3.6 - Prob. 55SRCh. 3.6 - Prob. 56SRCh. 3.6 - Prob. 57SRCh. 3.6 - Prob. 58SRCh. 3.6 - Prob. 59SRCh. 3.6 - Prob. 60SRCh. 3.6 - Prob. 61SRCh. 3.6 - Prob. 62SRCh. 3.6 - Prob. 63SCh. 3.6 - Prob. 64SCh. 3.6 - Prob. 65SCh. 3.6 - Prob. 1ECh. 3.6 - Prob. 2ECh. 3.6 - Prob. 3ECh. 3.6 - Prob. 4ECh. 3.6 - Prob. 5ECh. 3.6 - Prob. 6ECh. 3.6 - Prob. 7ECh. 3.6 - Prob. 8ECh. 3.6 - Prob. 9ECh. 3.6 - Prob. 10ECh. 3.6 - Prob. 11ECh. 3.6 - Prob. 12ECh. 3.6 - Prob. 13ECh. 3.6 - Prob. 14ECh. 3.7 - Prob. 1AGPCh. 3.7 - Prob. 1BGPCh. 3.7 - Prob. 2AGPCh. 3.7 - Prob. 2BGPCh. 3.7 - Prob. 3GPCh. 3.7 - Prob. 4AGPCh. 3.7 - Prob. 4BGPCh. 3.7 - Prob. 5AGPCh. 3.7 - Prob. 5BGPCh. 3.7 - Prob. 1CYUCh. 3.7 - Prob. 2CYUCh. 3.7 - Prob. 3CYUCh. 3.7 - Prob. 4CYUCh. 3.7 - Prob. 5CYUCh. 3.7 - Prob. 6CYUCh. 3.7 - Prob. 7CYUCh. 3.7 - Prob. 8CYUCh. 3.7 - Prob. 9CYUCh. 3.7 - Prob. 10CYUCh. 3.7 - Prob. 11CYUCh. 3.7 - Prob. 12CYUCh. 3.7 - Prob. 13CYUCh. 3.7 - Prob. 14CYUCh. 3.7 - Prob. 15CYUCh. 3.7 - Prob. 16CYUCh. 3.7 - Prob. 17CYUCh. 3.7 - Prob. 18CYUCh. 3.7 - Prob. 19CYUCh. 3.7 - Prob. 20CYUCh. 3.7 - Prob. 21CYUCh. 3.7 - Prob. 22CYUCh. 3.7 - Prob. 23CYUCh. 3.7 - Prob. 24CYUCh. 3.7 - Prob. 25CYUCh. 3.7 - Prob. 26PPSCh. 3.7 - Prob. 27PPSCh. 3.7 - Prob. 28PPSCh. 3.7 - Prob. 29PPSCh. 3.7 - Prob. 30PPSCh. 3.7 - Prob. 31PPSCh. 3.7 - Prob. 32PPSCh. 3.7 - Prob. 33PPSCh. 3.7 - Prob. 34PPSCh. 3.7 - Prob. 35PPSCh. 3.7 - Prob. 36PPSCh. 3.7 - Prob. 37PPSCh. 3.7 - Prob. 38PPSCh. 3.7 - Prob. 39PPSCh. 3.7 - Prob. 40PPSCh. 3.7 - Prob. 41PPSCh. 3.7 - Prob. 42PPSCh. 3.7 - Prob. 43PPSCh. 3.7 - Prob. 44PPSCh. 3.7 - Prob. 45PPSCh. 3.7 - Prob. 46PPSCh. 3.7 - Prob. 47PPSCh. 3.7 - Prob. 48PPSCh. 3.7 - Prob. 49PPSCh. 3.7 - Prob. 50PPSCh. 3.7 - Prob. 51PPSCh. 3.7 - Prob. 52PPSCh. 3.7 - Prob. 53PPSCh. 3.7 - Prob. 54PPSCh. 3.7 - Prob. 55PPSCh. 3.7 - Prob. 56HPCh. 3.7 - Prob. 57HPCh. 3.7 - Prob. 58HPCh. 3.7 - Prob. 59HPCh. 3.7 - Prob. 60HPCh. 3.7 - Prob. 61HPCh. 3.7 - Prob. 62STPCh. 3.7 - Prob. 63STPCh. 3.7 - Prob. 64STPCh. 3.7 - Prob. 65STPCh. 3.7 - Prob. 66SRCh. 3.7 - Prob. 67SRCh. 3.7 - Prob. 68SRCh. 3.7 - Prob. 69SRCh. 3.7 - Prob. 70SRCh. 3.7 - Prob. 71SRCh. 3.7 - Prob. 72SRCh. 3.7 - Prob. 73SCh. 3.7 - Prob. 74SCh. 3.7 - Prob. 75SCh. 3.8 - Prob. 1GPCh. 3.8 - Prob. 2AGPCh. 3.8 - Prob. 2BGPCh. 3.8 - Prob. 3GPCh. 3.8 - Prob. 1CYUCh. 3.8 - Prob. 2CYUCh. 3.8 - Prob. 3CYUCh. 3.8 - Prob. 4CYUCh. 3.8 - Prob. 5CYUCh. 3.8 - Prob. 6CYUCh. 3.8 - Prob. 7CYUCh. 3.8 - Prob. 8CYUCh. 3.8 - Prob. 9CYUCh. 3.8 - Prob. 10CYUCh. 3.8 - Prob. 11CYUCh. 3.8 - Prob. 12CYUCh. 3.8 - Prob. 13PPSCh. 3.8 - Prob. 14PPSCh. 3.8 - Prob. 15PPSCh. 3.8 - Prob. 16PPSCh. 3.8 - Prob. 17PPSCh. 3.8 - Prob. 18PPSCh. 3.8 - Prob. 19PPSCh. 3.8 - Prob. 20PPSCh. 3.8 - Prob. 21PPSCh. 3.8 - Prob. 22PPSCh. 3.8 - Prob. 23PPSCh. 3.8 - Prob. 24PPSCh. 3.8 - Prob. 25PPSCh. 3.8 - Prob. 26PPSCh. 3.8 - Prob. 27PPSCh. 3.8 - Prob. 28PPSCh. 3.8 - Prob. 29PPSCh. 3.8 - Prob. 30PPSCh. 3.8 - Prob. 31PPSCh. 3.8 - Prob. 32PPSCh. 3.8 - Prob. 33PPSCh. 3.8 - Prob. 34PPSCh. 3.8 - Prob. 35PPSCh. 3.8 - Prob. 36PPSCh. 3.8 - Prob. 37PPSCh. 3.8 - Prob. 38HPCh. 3.8 - Prob. 39HPCh. 3.8 - Prob. 40HPCh. 3.8 - Prob. 41HPCh. 3.8 - Prob. 42HPCh. 3.8 - Prob. 43STPCh. 3.8 - Prob. 44STPCh. 3.8 - Prob. 45STPCh. 3.8 - Prob. 46STPCh. 3.8 - Prob. 47SRCh. 3.8 - Prob. 48SRCh. 3.8 - Prob. 49SRCh. 3.8 - Prob. 50SRCh. 3.8 - Prob. 51SRCh. 3.8 - Prob. 52SRCh. 3.8 - Prob. 53SRCh. 3.8 - Prob. 54SCh. 3.8 - Prob. 55SCh. 3.8 - Prob. 56SCh. 3.8 - Prob. 1ECh. 3.8 - Prob. 2ECh. 3.8 - Prob. 3ECh. 3.8 - Prob. 4ECh. 3.8 - Prob. 5ECh. 3.8 - Prob. 6ECh. 3 - Prob. 1QCCh. 3 - Prob. 2QCCh. 3 - Prob. 3QCCh. 3 - Prob. 4QCCh. 3 - Prob. 5QCCh. 3 - Prob. 6QCCh. 3 - Prob. 7QCCh. 3 - Prob. 8QCCh. 3 - Prob. 9QCCh. 3 - Prob. 10QCCh. 3 - Prob. 11QCCh. 3 - Prob. 12QCCh. 3 - Prob. 13QCCh. 3 - Prob. 14QCCh. 3 - Prob. 1SGRCh. 3 - Prob. 2SGRCh. 3 - Prob. 3SGRCh. 3 - Prob. 4SGRCh. 3 - Prob. 5SGRCh. 3 - Prob. 6SGRCh. 3 - Prob. 7SGRCh. 3 - Prob. 8SGRCh. 3 - Prob. 9SGRCh. 3 - Prob. 10SGRCh. 3 - Prob. 11SGRCh. 3 - Prob. 12SGRCh. 3 - Prob. 13SGRCh. 3 - Prob. 14SGRCh. 3 - Prob. 15SGRCh. 3 - Prob. 16SGRCh. 3 - Prob. 17SGRCh. 3 - Prob. 18SGRCh. 3 - Prob. 19SGRCh. 3 - Prob. 20SGRCh. 3 - Prob. 21SGRCh. 3 - Prob. 22SGRCh. 3 - Prob. 23SGRCh. 3 - Prob. 24SGRCh. 3 - Prob. 25SGRCh. 3 - Prob. 26SGRCh. 3 - Prob. 27SGRCh. 3 - Prob. 28SGRCh. 3 - Prob. 29SGRCh. 3 - Prob. 30SGRCh. 3 - Prob. 31SGRCh. 3 - Prob. 32SGRCh. 3 - Prob. 33SGRCh. 3 - Prob. 34SGRCh. 3 - Prob. 35SGRCh. 3 - Prob. 36SGRCh. 3 - Prob. 37SGRCh. 3 - Prob. 38SGRCh. 3 - Prob. 39SGRCh. 3 - Prob. 40SGRCh. 3 - Prob. 41SGRCh. 3 - Prob. 42SGRCh. 3 - Prob. 43SGRCh. 3 - Prob. 44SGRCh. 3 - Prob. 45SGRCh. 3 - Prob. 46SGRCh. 3 - Prob. 47SGRCh. 3 - Prob. 48SGRCh. 3 - Prob. 1PTCh. 3 - Prob. 2PTCh. 3 - Prob. 3PTCh. 3 - Prob. 4PTCh. 3 - Prob. 5PTCh. 3 - Prob. 6PTCh. 3 - Prob. 7PTCh. 3 - Prob. 8PTCh. 3 - Prob. 9PTCh. 3 - Prob. 10PTCh. 3 - Prob. 11PTCh. 3 - Prob. 12PTCh. 3 - Prob. 13PTCh. 3 - Prob. 14PTCh. 3 - Prob. 15PTCh. 3 - Prob. 16PTCh. 3 - Prob. 17PTCh. 3 - Prob. 18PTCh. 3 - Prob. 19PTCh. 3 - Prob. 20PTCh. 3 - Prob. 21PTCh. 3 - Prob. 22PTCh. 3 - Prob. 1ECh. 3 - Prob. 2ECh. 3 - Prob. 3ECh. 3 - Prob. 4ECh. 3 - Prob. 5ECh. 3 - Prob. 6ECh. 3 - Prob. 7ECh. 3 - Prob. 8ECh. 3 - Prob. 1STPCh. 3 - Prob. 2STPCh. 3 - Prob. 3STPCh. 3 - Prob. 4STPCh. 3 - Prob. 5STPCh. 3 - Prob. 6STPCh. 3 - Prob. 7STPCh. 3 - Prob. 8STPCh. 3 - Prob. 9STPCh. 3 - Prob. 10STPCh. 3 - Prob. 11STPCh. 3 - Prob. 12STPCh. 3 - Prob. 13STP

Additional Math Textbook Solutions

Find more solutions based on key concepts
ASSESSMENT A sheet of paper is cut into 5 same-size parts. Each of the parts is then cut into 5 same-size parts...

A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)

Find how many SDs above the mean price would be predicted to cost.

Intro Stats, Books a la Carte Edition (5th Edition)

The distance between the Ashland and Bowling green   (82∘W,38∘N)and(86∘W,35∘N)

Pre-Algebra Student Edition

A pair of fair dice is rolled. What is the probability that the second die lands on a higher value than does th...

A First Course in Probability (10th Edition)

Ages A study of all the students at a small college showed a mean age of 20.7 and a standard deviation of 2.5 y...

Introductory Statistics

The following set of data is from sample of n=5: a. Compute the mean, median, and mode. b. Compute the range, v...

Basic Business Statistics, Student Value Edition

Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Text book image
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Text book image
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Text book image
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
Text book image
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
SEE MORE TEXTBOOKS
Points, Lines, Planes, Segments, & Rays - Collinear vs Coplanar Points - Geometry; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=dDWjhRfBsKM;License: Standard YouTube License, CC-BY
Naming Points, Lines, and Planes; Author: Florida PASS Program;https://www.youtube.com/watch?v=F-LxiLSSaLg;License: Standard YouTube License, CC-BY