
A water trough of semicircular cross section of radius 0.6 m consists of two symmetric parts hinged to each other at the bottom, as shown in Fig. P3-72. The two pans are held together by a cable and turnbuckle placed every 3 m along the length of the trough. Calculate the tension in each cable when the trough is filled to the rim.
The tension in the cable.
Answer to Problem 79P
The tension in the cable is
Explanation of Solution
Given information:
A water trough of semicircular cross section of two symmetric parts hinged at each other at the bottom and held together by a cable.
The figure below shows the free body diagram of the right-hand side part of water trough.
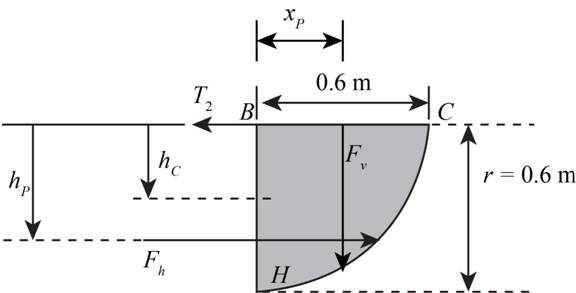
Figure-(1)
Write the Equation for the horizontal hydrostatic force on the part.
Here, density of fluid is
Write the Equation for vertical projected area.
Here, radius of the quarter circle is
Substitute
Write the Equation of the vertical force for curved surface.
Here volume of fluid above curved surface is
Write the Expression for volume of fluid above curved surface.
Substitute
Write the Expression for centre of pressure.
Write the Expression for moment of Inertia.
Substitute
Write the moment Equation about the hinge point.
Here, distance between the line of action of vertical force and hinged point is
Write the Expression for distance between the line of action of vertical force and hinged point.
Substitute
The figure below shows the free body diagram of water trough.
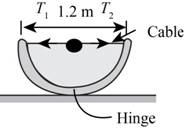
Figure-(2)
Write the expression for horizontal force equilibrium.
Figure-(2)
Calculation:
Substitute
Substitute,
Substitute
Substitute
Substitute
Substitute
Substitute
Here the tension value is same
Conclusion:
The tension in the cable is
Want to see more full solutions like this?
Chapter 3 Solutions
Fluid Mechanics Fundamentals And Applications
- A close end tube of thin-walled circular section may be subjected to torque Tand internal pressure P, as shown in Figure Q3. The shear stress in the wall caused by the torque can be calculated as σ = T/(2πR²t), where the mean radius of the cross section is R(i.e., the radius of the centreline of the wall) and the wall thickness is t. The internal radius of the tube can be calculated as (R-t/2). However, as R>> t, you can approximately assume that the internal radius of the tube is equal to Rin the subsequent calculation. The tube is made from a material with Young's modulus E, Poisson's ratio v. Orr T Ozz бее буг Z бее T бел Figure Q3 Centreline of the wall Rarrow_forwardA bar of length L and of a circular cross-section of diameter D is clamped at the top end and loaded at the other (bottom) end by a point load P as shown in Figure Q2a. The cross-section of the bar is shown in Figure Q2b indicating that load is applied at the point A. The material used in the bar has specific weight y. Find the magnitude and location of the maximum normal stress in the bar. Figure Q2 a Figure Q2 b 45° Aarrow_forward(If L=3508 mm, W-9189 N, E=80 GPa, Determine the deflection at the free end of the beam.) Step-4 Which equation in the following choices most accurately represents the functional relationship between the value of the deflection, Vmax ( Units: mm) at the free end (XL) of the beam and the second moment of area about z-axis, Izz (Units: mm²) of the cross section ? (Please note that " X = L/2" is the same as "X = L ÷ 2" .) Select one: O 1. Vmax 1776823249.026 / Izz O 2. Vmax 516518386.345/Izz O 3. Vmax=743786476.336/Izz O 4. Vmax 1002045669.509/Izz O 5. Vmax 330571767.261/Izz O 6. Vmax 196276986.811 / Izz O 7. Vmax 1435921114.038/Izzarrow_forward
- The second moment of area about z-axis of the cross section, Izz ( Units: mm4) can be calculated as Select one: O 1. 2.081 x 107 ○ 2. 2.281x 107 ○ 3. 2.201 x 107 ○ 4. 1.348x 107 ○ 5. 1.466 x107 ○ 6. 1.966x107 O 7. 1.833 x 107 O 8. 1.109x 107arrow_forward[(a) If the change of the diameter cannot exceed 0.1 m under elastic deformation, calculate the minimum allowable wall thickness of the cylindrical pressure vessel. (P=23.6 MPa, T=0 KN.m, R = 2 m, Young's modulus E = 246 GPa, and Poisson's ratio v = 0.21)] Step-3 The functional relationship between the change of the diameter, DD (units: mm), and wall thickness t(units: mm) can be most accurately expressed as Select one: O 1. DD-282.688/t O 2. DD=424.033/t O 3. DD=343.447/t 4. DD = 686.894/t O 5. DD=1696.130/t O 6. DD-228.965/t 7. DD=848.065/t 8. DD=1373.789/tarrow_forwardA bar of length L and of a circular cross-section of diameter D is clamped at the top end and loaded at the other (bottom) end by a point load P as shown in Figure Q2a. The cross-section of the bar is shown in Figure Q2b indicating that load is applied at the point A. The material used in the bar has specific weight y. Find the magnitude and location of the maximum normal stress in the bar. Z Figure Q2 a Figure Q2 b 45° Aarrow_forward
- A close end tube of thin-walled circular section may be subjected to torque Tand internal pressure P, as shown in Figure Q3. The shear stress in the wall caused by the torque can be calculated as T = T/(2πR²t), where the mean radius of the cross section is R(i.e., the radius of the centreline of the wall) and the wall thickness is t. The internal radius of the tube can be calculated as (R-t/2). However, as R>>t, you can approximately assume that the internal radius of the tube is equal to Rin the subsequent calculation. The tube is made from a material with Young's modulus E, Poisson's ratio v. T Centreline of the wall R P Ozz бөө Orr Z бут бее Ozz Figure Q3 (a) If the change of the diameter cannot exceed 0.1 m under elastic deformation, calculate the minimum allowable wall thickness of the cylindrical pressure vessel if P=23.6 MPa, T=0 KN.m, R = 2 m, Young's modulus E = 246 GPa, and Poisson's ratio v = 0.21. Step-1 the functional relationships between hoop stress σ and wall thickness…arrow_forwardA cantilever beam of a channel section and length L is loaded by a point load W applied at half-length of the beam through the centroid of the section, as shown in Figure Q1. The material of the beam is aluminum alloy with the Young’s modulus of E .arrow_forwardA bar of length L and of a circular cross-section of diameter D is clamped at the top end and loaded at the other (bottom) end by a point load P as shown in Figure Q2a. The cross-section of the bar is shown in Figure Q2b indicating that load is applied at the point A. The material used in the bar has specific weight y. Find the magnitude and location of the maximum normal stress in the bar. Figure Q2 a Figure Q2 b 45°arrow_forward
- Question2 The mission profile for a jet driven aircraft consists of the following segments: engine start and warm-up, taxi, take-off, climb to the cruise altitude of 35000 ft, descend to 10000 ft, one hour loiter at this altitude at 60% of the cruise speed, flight at loiter speed and altitude to an alternate airport (100 nm), descend to landing approach condition followed by the final landing, taxi and shutdown. The cruise Mach number is 0.8. No provisions are made for the reserved fuel or any trapped oil and fuel. The aircraft carries 200 people (including pilots and the cabin crew) at 175 lb each and 90 lb baggage each. This aircraft has a wing area of 2000 ft² a) If the landing stall speed of the aircraft is set at 100 kts corresponding to a landing weight of 0.85 Wro, and C(Lmax) Landing = 2.50, determine take-off weight and then calculate the range and empty weight of this aircraft (see Table Q2). Consider landing at sea level on a standard day. L/D at cruise L/D at 10000ft flight…arrow_forwardq Y X A ΕΙ L B Marrow_forwardIf L=3508 mm, W-9189 N, E=80 GPa, Determine the deflection at the free end of the beam. Step-1 The bend moment of the beam, M (Units: N.m), as a function of spatial coordinate X ( Units: m) can be described by Select one: O 1. M = 16117.506 +9189.000*X, for 0<=X<= L/2; M=0.00, for L/2< x <= L O 2. M = 16117506.000 - 9189.000*X, for 0<= x <= L/2; M = 9189.000* X, for L/2< x <= L O 3. M=16117.5069189.000*X, for 0<=X<= L/2; M=0.00, for L/2< x <= L O 4. M = 16117506.000 + 9189.000*X, for 0<=X<= L/2; M = 9189.000*X, for L/2arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
