Chapter 3, Problem 72P

A gear reduction unit uses the countershaft shown in the figure. Gear A receives power from another gear with the transmitted force F_A applied at the 20° pressure angle as shown. The power is transmitted through the shaft and delivered through gear B through a transmitted force F_B at the pressure angle shown.

(a) Determine the force F_B, assuming the shaft is running at a constant speed.

(b) Find the bearing reaction forces, assuming the bearings act as simple supports.

(c) Draw shear-force and bending-moment diagrams for the shaft. If needed, make one set for the horizontal plane and another set for the vertical plane.

(d) At the point of maximum bending moment, determine the bending stress and the torsional shear stress.

(e) At the point of maximum bending moment, determine the principal stresses and the maximum shear stress.

Problem 3–72*

To determine

The magnitude of the force acting on the wheel B.

Answer to Problem 72P

The magnitude of the force acting on the wheel B is $750\text{lbf}$.

Explanation of Solution

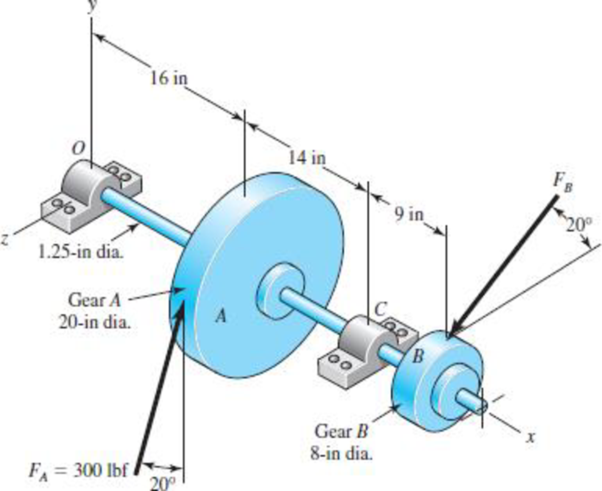
The figure below shows the free body diagram of pulley A.

Figure-(1)

The figure below shows the free body diagram of pulley B.

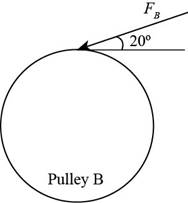
Figure-(2)

Calculate the force $F_B$, using the net torque equation.

    $\begin{array}{l}{\displaystyle \sum T}=0\\ -\left(F_A\times \frac{d_A}{2}\times \cos {\theta }_1\right)+\left(F_B\times \frac{d_B}{2}\times \cos {\theta }_2\right)=0\\ F_B=F_A\frac{d_A\cos {\theta }_1}{d_B\cos {\theta }_2}\end{array}$ (I)

Here, the force acting on pulley $A$ is $F_A$, the diameter of pulley $A$ is $d_A$, the angle at which force acts on pulley $A$ is ${\theta }_1$, the force acting on pulley $B$ is $F_B$, the diameter of pulley $B$ is $d_B$ and the angle at which force acts on pulley $B$ is ${\theta }_2$.

Conclusion:

Substitute $300\text{lbf}$ for $F_A$, $20\text{in}$ for $d_A$, $20°$ for ${\theta }_1$, $8\text{in}$ for $d_B$ and $20°$ for ${\theta }_2$ in Equation (I).

    $\begin{array}{c}{F}_B=\left(300\text{lbf}\right)\left(\frac{20\text{in}\times \cos 20°}{8\text{in}\times \cos 20°}\right)\\ =\left(300\text{lbf}\right)\left(\frac{20\text{in}}{8\text{in}}\right)\\ =750\text{lbf}\end{array}$

Thus, the force $F_B$, assuming the shaft is running at constant speed is $750\text{lbf}$.

To determine

The bearing reaction forces at the supports.

Answer to Problem 72P

The bearing reaction at $O$ is $332.73\text{lbf}$ and at $C$ is $880.74\text{lbf}$.

Explanation of Solution

Write the expression for moment about bearing $O$ in $z\text{-}$ direction.

    $\begin{array}{l}{\displaystyle \sum M_{Oz}}=0\\ \left[\left(F_A\cos {\theta }_1\times l_{OA}\right)-\left(F_B\sin {\theta }_2\times \left(l_{OA}+l_{AC}+l_{CB}\right)\right)+R_{Cy}\times \left(l_{OA}+l_{AC}\right)\right]=0\\ R_{Cy}=\frac{\left[\left(F_B\sin {\theta }_2\times \left(l_{OA}+l_{AC}+l_{CB}\right)\right)-\left(F_A\cos {\theta }_1\times l_{OA}\right)\right]}{\left(l_{OA}+l_{AC}\right)}\end{array}$ (II)

Here, the reaction force at bearing $C$ in $y\text{-}$ direction is $R_{Cy}$, the distance between $O$ and $A$ is $l_{OA}$, the distance between $A$ and $C$ is $l_{AC}$ and the distance between $C$ and $B$ is $l_{CB}$.

Write the equation to balance the forces in $y\text{-}$ direction.

    $\begin{array}{l}{\displaystyle \sum F_y}=0\\ R_{Oy}+F_A\cos {\theta }_1+R_{Cy}-F_B\sin {\theta }_2=0\\ R_{Oy}=F_B\sin {\theta }_2-R_{Cy}-F_A\cos {\theta }_1\end{array}$ (III)

Here, the reaction force at bearing $O$ in $y\text{-}$ direction is $R_{Oy}$.

Write the expression for moment about bearing $O$ in $y$-direction.

    $\begin{array}{l}{\displaystyle \sum M_{Oy}}=0\\ \left[\left(F_A\sin {\theta }_1\times l_{OA}\right)-\left(F_B\cos {\theta }_2\times \left(l_{OA}+l_{AC}+l_{CB}\right)\right)-R_{Cz}\left(l_{OA}+l_{AC}\right)\right]=0\\ R_{Cz}=\frac{\left[\left(F_A\sin {\theta }_1\times l_{OA}\right)-\left(F_B\cos {\theta }_2\left(l_{OA}+l_{AC}+l_{CB}\right)\right)\right]}{\left(l_{OA}+l_{AC}\right)}\end{array}$ (IV)

Here, the reaction force at bearing $C$ in $z$-direction is $R_{Cz}$.

Write the equation to balance the forces in $z$-direction.

    $\begin{array}{l}{\displaystyle \sum F_z}=0\\ R_{Oz}-F_A\sin {\theta }_1+R_{Cz}+F_B\cos {\theta }_2=0\\ R_{Oz}=F_A\sin {\theta }_1-R_{Cz}-F_B\cos {\theta }_2\end{array}$ (V)

Here, the reaction force at bearing $O$ in $z$-direction is $R_{Oz}$.

Calculate the reaction forces at bearing $O$.

    $R_O=\sqrt{R_{Oy}^2+R_{Oz}^2}$ (VI)

Here, the reaction force at bearing $O$ is $R_O$.

Calculate the reaction forces at bearing $C$.

    $R_C=\sqrt{R_{Cy}^2+R_{Cz}^2}$ (VII)

Here, the reaction force at bearing $C$ is $R_C$.

Conclusion:

Substitute $750\text{lbf}$ for $F_B$, $20°$ for ${\theta }_1$, $300\text{lbf}$ for $F_A$, $20°$ for ${\theta }_2$, $16\text{in}$ for $l_{OA}$, $14\text{in}$ for $l_{AC}$ and $9\text{in}$ for $l_{CB}$ in Equation (II).

    $\begin{array}{c}{R}_{Cy}=\frac{\left[\left(750\text{lbf}\times \sin 20°\times \left(16\text{in}+14\text{in}+9\text{in}\right)\right)-\left(300\text{lbf}\times \cos 20°\times 16\text{in}\right)\right]}{\left(16\text{in}+14\text{in}\right)}\\ =\frac{\left[\left(750\text{lbf}\times \sin 20°\times \left(39\text{in}\right)\right)-\left(300\text{lbf}\times \cos 20°\times 16\text{in}\right)\right]}{\left(30\text{in}\right)}\\ =183.1\text{lbf}\end{array}$

Substitute $750\text{lbf}$ for $F_B$, $20°$ for ${\theta }_2$, $183.1\text{lbf}$ for $R_{Cy}$, $300\text{lbf}$ for $F_A$ and $20°$ for ${\theta }_1$ in Equation (III).

    $\begin{array}{c}{R}_{Oy}=750\text{lbf}\sin \left(20°\right)-183.1\text{lbf}-300\cos \left(20°\right)\\ =256.51\text{lbf}-183.1\text{lbf}-281.90\text{lbf}\\ =-208.49\text{lbf}\\ \approx -208.50\text{lbf}\end{array}$

Substitute $750\text{lbf}$ for $F_B$, $20°$ for ${\theta }_1$, $300\text{lbf}$ for $F_A$, $20°$ for ${\theta }_2$, $16\text{in}$ for $l_{OA}$, $14\text{in}$ for $l_{AC}$ and $9\text{in}$ for $l_{CB}$ in Equation (IV).

    $\begin{array}{c}{R}_{Cz}=\frac{\left[\left(750\text{lbf}\times \cos 20°\times \left(16\text{in}+14\text{in}+9\text{in}\right)\right)-\left(300\text{lbf}\times \sin 20°\times 16\text{in}\right)\right]}{\left(16\text{in}+14\text{in}\right)}\\ =\frac{\left[\left(750\text{lbf}\times \cos 20°\times \left(39\text{in}\right)\right)-\left(300\text{lbf}\times \sin 20°\times 16\text{in}\right)\right]}{\left(30\text{in}\right)}\\ =-861.5\text{lbf}\end{array}$

Substitute $300\text{lbf}$ for $F_A$, $20°$ for ${\theta }_1$, $-861.5\text{lbf}$ for $R_{Cz}$, $750\text{lbf}$ for $F_B$ and $20°$ for ${\theta }_2$ in Equation (V).

    $\begin{array}{c}{R}_{Oz}=\left(300\text{lbf}\times \sin 20°\right)-\left(-861.5\text{lbf}\right)-\left(750\text{lbf}\times \cos 20°\right)\\ =\left(102.60\text{lbf}\right)-\left(-861.5\text{lbf}\right)-\left(704.77\text{lbf}\right)\\ =259.33\text{lbf}\\ \approx 259.3\text{lbf}\end{array}$

Substitute $-208.5\text{lbf}$ for $R_{Oy}$ and $259.3\text{lbf}$ for $R_{Oz}$ in Equation (VI).

    $\begin{array}{c}{R}_O=\sqrt{{\left(-208.5\text{lbf}\right)}^2+{\left(259.3\text{lbf}\right)}^2}\\ =\sqrt{43472.25+67236.49}\text{lbf}\\ \approx 332.73\text{lbf}\end{array}$

Thus, the bearing reaction at $O$ is $332.73\text{lbf}$.

Substitute $183.1\text{lbf}$ for $R_{Cy}$ and $-861.5\text{lbf}$ for $R_{Cz}$ in Equation (VII).

    $\begin{array}{c}{R}_C=\sqrt{{\left(183.1\text{lbf}\right)}^2+{\left(-861.5\text{lbf}\right)}^2}\\ =\sqrt{33525.61+742182.25}\text{lbf}\\ =880.74\text{lbf}\end{array}$

Thus, the bearing reaction force at $C$ is $880.74\text{lbf}$.

To determine

The shear force and bending moment diagram for the shaft.

Answer to Problem 72P

The shear force and bending moment diagram for the shaft in $y\text{-}$ direction is shown below.

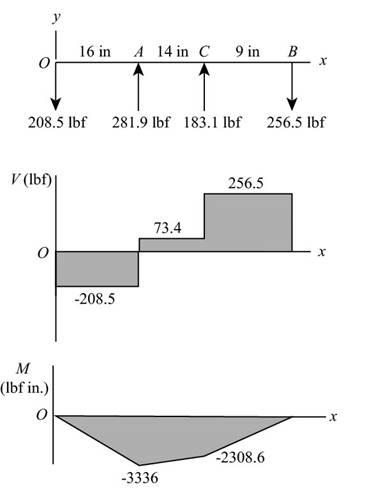
The shear force and bending moment diagram for the shaft in $z\text{-}$ direction is shown below.

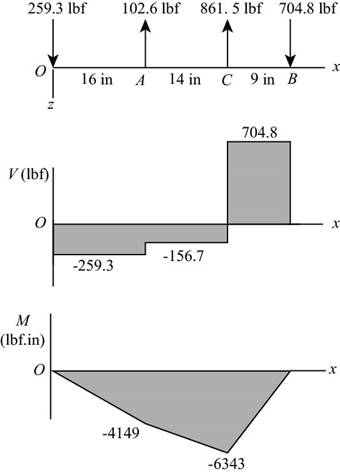
Explanation of Solution

The calculations for shear force and bending moment diagram in $y$ direction.

Calculate the shear force at $O$ in $y$ direction.

    $S{F}_{Oy}=R_{Oy}$ (VIII)

Here, the shear force at $O$ in $y$ direction is $S{F}_{Oy}$.

Calculate the shear force at $A$ in $y$ direction.

    $S{F}_{Ay}=S{F}_{Oy}+F_A\cos {\theta }_1$ (IX)

Here, the shear force at $A$ in $y$ direction is $S{F}_{Ay}$.

Calculate the shear force at $C$ in $y$ direction.

    $S{F}_{Cy}=S{F}_{Ay}+R_{Cy}$ (X)

Here, the shear force at $C$ in $y$ direction is $S{F}_{Cy}$.

Calculate the shear force at $B$ in $y$ direction.

    $S{F}_{By}=S{F}_{Cy}-F_B\sin {\theta }_2$ (XI)

Here, the shear force at $B$ in $y$ direction is $S{F}_{By}$.

Calculate the moment at $O$ and $B$.

    $M_O=M_B=0$ (XII)

Here, the moment at $O$ is $M_O$ and the moment at $B$ is $M_B$.

Calculate the moment at $A$ in $y$-direction.

    $M_{Ay}=S{F}_{Oy}\times l_{OA}$ (XIII)

Here, the moment at $A$ in $y$-direction is $M_A$.

Calculate the moment at $C$ in $y$-direction.

    $M_{Cy}=F_B\sin {\theta }_2\times l_{CB}$ (XIV)

Here, the moment at $C$ in $y$ direction is $M_{Cy}$.

The calculations for shear force and bending moment diagram in $z\text{-}$ direction.

Calculate the shear force at $O$ in $z$-direction.

    $S{F}_{Oz}=-R_{Oz}$ (XV)

Here, the shear force at $O$ in $z$-direction is $S{F}_{Oz}$.

Calculate the shear force at $A$ in $z$-direction.

    $S{F}_{Az}=S{F}_{Oz}+F_A\sin {\theta }_1$ (XVI)

Here, the shear force at $A$ in $z$-direction is $S{F}_{Az}$.

Calculate the shear force at $C$ in $z$-direction.

    $S{F}_{Cz}=S{F}_{Az}-R_{Cz}$ (XVII)

Here, the shear force at $C$ in $z$-direction is $S{F}_{Cz}$.

Calculate the shear force at $B$ in $z$-direction.

    $S{F}_{Bz}=S{F}_{Cz}-F_B\cos {\theta }_2$ (XVIII)

Here, the shear force at $B$ in $z$ direction is $S{F}_{Bz}$.

Calculate the moment at $O$ and $B$.

    $M_O=M_B=0$ (XIX)

Here, the moment at $O$ is $M_O$ and the moment at $B$ is $M_B$.

Calculate the moment at $A$ in $z$-direction.

    $M_{Az}=S{F}_{Oz}\times l_{OA}$ (XX)

Here, the moment at $A$ in $z$-direction is $M_{Az}$.

Calculate the moment at $C$ in $z$-direction.

    $M_{Cz}=-F_B\cos {\theta }_2\times l_{CB}$ (XXI)

Here, the moment at $C$ in $z$-direction is $M_{Cz}$.

Conclusion:

Substitute $-208.5\text{lbf}$ for $R_{Oy}$ in Equation (VIII).

    $S{F}_{Oy}=-208.5\text{lbf}$

Substitute $-208.5\text{lbf}$ for $S{F}_{Oy}$, $300\text{lbf}$ for $F_A$ and $20°$ for ${\theta }_1$ in Equation (IX).

    $\begin{array}{c}S{F}_{Ay}=-208.5\text{lbf}+\left(300\text{lbf}\times \cos 20°\right)\\ =-208.5\text{lbf}+\left(281.90\text{lbf}\right)\\ =73.4\text{lbf}\end{array}$

Substitute $73.4\text{lbf}$ for $S{F}_{Ay}$ and $183.1\text{lbf}$ for $R_C$ in Equation (X).

    $\begin{array}{c}S{F}_{Cy}=73.4\text{lbf}+183.1\text{lbf}\\ =256.5\text{lbf}\end{array}$

Substitute $256.5\text{lbf}$ for $S{F}_{Cy}$, $750\text{lbf}$ for $F_B$ and $20°$ for ${\theta }_2$ in Equation (XI).

    $\begin{array}{c}S{F}_{By}=256.5\text{lbf}-\left(750\text{lbf}\times \sin 20°\right)\\ =256.5\text{lbf}-\left(256.5\text{lbf}\right)\\ =0\text{lbf}\end{array}$

Substitute $-208.5\text{lbf}$ for $S{F}_{Oy}$ and $16\text{in}$ for $l_{OA}$ in Equation (XIII).

    $\begin{array}{c}{M}_{Ay}=-208.5\text{lbf}\times 16\text{in}\\ =-3336\text{lbf}\cdot \text{in}\end{array}$

Substitute $750\text{lbf}$ for $F_B$, $20°$ for ${\theta }_2$ and $9\text{in}$ for $l_{CB}$ in Equation (XIV).

    $\begin{array}{c}{M}_{Cy}=-\left(750\text{lbf}\times \sin 20°\right)\times 9\text{in}\\ =-2308.5\text{lbf}\cdot \text{in}\end{array}$

Thus, the shear force and bending moment diagram in $y\text{-}$ direction is as follow.

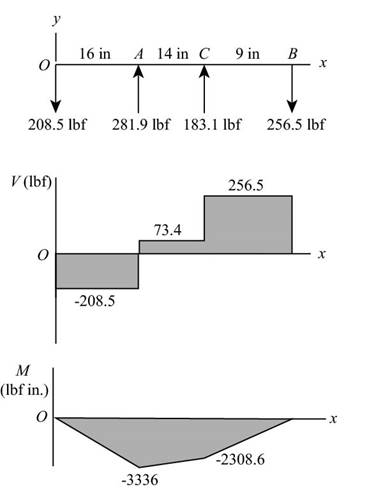
Figure-(3)

Substitute $259.3\text{lbf}$ for $R_{Oz}$ in Equation (XV).

    $S{F}_{Oz}=-259.3\text{lbf}$

Substitute $-259.3\text{lbf}$ for $S{F}_{Oz}$, $300\text{lbf}$ for $F_A$ and $20°$ for ${\theta }_1$ in Equation (XVI).

    $\begin{array}{c}S{F}_{Az}=-259.3\text{lbf}+\left(300\text{lbf}\times \sin 20°\right)\\ =-156.7\text{lbf}\end{array}$

Substitute $-156.7\text{lbf}$ for $S{F}_{Az}$ $-861.5\text{lbf}$ for $R_{Cz}$ in Equation (XVII).

    $\begin{array}{c}S{F}_{Cz}=-156.7\text{lbf}-\left(-861.5\text{lbf}\right)\\ =704.8\text{lbf}\end{array}$

Substitute $704.8\text{lbf}$ for $S{F}_{Cz}$, $750\text{lbf}$ for $F_B$ and $20°$ for ${\theta }_2$ in Equation (XVIII).

    $\begin{array}{c}S{F}_{Bz}=704.8\text{lbf}-\left(750\text{lbf}\times \cos 20\right)\\ =0\text{lbf}\end{array}$

Substitute $-259.3\text{lbf}$ for $S{F}_{Oz}$ and $16\text{in}$ for $l_{OA}$ in Equation (XX).

    $\begin{array}{c}{M}_{Az}=-259.3\text{lbf}\times 16\text{in}\\ =-4148.8\text{lbf}\cdot \text{in}\\ \approx -4149\text{lbf}\cdot \text{in}\end{array}$

Substitute $750\text{lbf}$ for $F_B$, $20°$ for ${\theta }_2$ and $9\text{in}$ for $l_{CB}$ in Equation (XXI).

    $\begin{array}{c}{M}_{Cz}=-\left(750\text{lbf}\times \cos 20°\right)\times 9\text{in}\\ =-6343\text{lbf}\cdot \text{in}\end{array}$

Thus, the shear force and bending moment diagram in $z\text{-}$ direction is as follows.

Figure-(4)

To determine

The bending stress at point of maximum bending moment.

The shear stress at point of maximum bending moment.

Answer to Problem 72P

The bending stress at point of maximum bending moment is $35.2\text{kpsi}$.

The shear stress at point of maximum bending moment is $7.35\text{kpsi}$.

Explanation of Solution

Write the net moment at $A$.

    $M_A=\sqrt{M_{Ay}^2+M_{Az}^2}$ (XXII)

Here, the net moment at $A$ is $M_A$.

Write the net moment at $C$.

    $M_C=\sqrt{M_{Cy}^2+M_{Cz}^2}$ (XXIII)

Here, the net moment at $C$ is $M_C$.

Write the torque transmitted by shaft from $A$ to $B$.

    $T=F_A\cos {\theta }_1\times \frac{d_A}{2}$ (XXIV)

Here, the torque transmitted by shaft from $A$ to $B$ is $T$.

Calculate the bending stress.

    $\sigma =\frac{32M_C}{\pi d^3}$ (XXV)

Here, the bending stress is $\sigma$ and diameter of shaft is $d$.

Calculate the shear stress.

    $\tau =\frac{16T}{\pi d^3}$ (XVI)

Here, the shear stress is $\tau$.

Conclusion:

Substitute $-3336\text{lbf}\cdot \text{in}$ for $M_{Ay}$ and $-4149\text{lbf}\cdot \text{in}$ for $M_{Az}$ in Equation (XXII).

    $\begin{array}{c}{M}_A=\sqrt{{\left(-3336\text{lbf}\cdot \text{in}\right)}^2+{\left(-4149\text{lbf}\cdot \text{in}\right)}^2}\\ =\sqrt{28343097}\text{lbf}\cdot \text{in}\\ \approx 5324\text{lbf}\cdot \text{in}\end{array}$

Substitute $-2308.5\text{lbf}\cdot \text{in}$ for $M_{Cy}$ and $-6343\text{lbf}\cdot \text{in}$ for $M_{Cz}$ in Equation (XXIII).

    $\begin{array}{c}{M}_C=\sqrt{{\left(-2308.5\text{lbf}\cdot \text{in}\right)}^2+{\left(-6343\text{lbf}\cdot \text{in}\right)}^2}\\ =\sqrt{45562821.25}\text{lbf}\cdot \text{in}\\ \approx 6750\text{lbf}\cdot \text{in}\end{array}$

Since $M_C>M_A$, so the critical location is at point C.

Substitute $300\text{lbf}$ for $F_A$, $20°$ for ${\theta }_1$ and $20\text{in}$ for $d_A$ in Equation (XXIV).

    $\begin{array}{c}T=300\text{lbf}\times \cos 20°\times \frac{20\text{in}}{2}\\ =300\text{lbf}\times \cos 20°\times 10\text{in}\\ =2819\text{lbf}\cdot \text{in}\end{array}$

Substitute $6750\text{lbf}\cdot \text{in}$ for $M_C$ and $1.25\text{in}$ for $d$ in Equation (XXV).

    $\begin{array}{c}\sigma =\frac{32\times 6750\text{lbf}\cdot \text{in}}{\pi {\left(1.25\text{in}\right)}^3}\\ =\frac{216000\text{lbf}\cdot \text{in}}{\pi {\left(1.25\text{in}\right)}^3}\\ =\left(35202.526\text{psi}\right)\left(\frac{1\text{kpsi}}{{10}^3\text{psi}}\right)\\ \approx 35.2\text{kpsi}\end{array}$

Thus, the bending stress at point of maximum bending moment is $35.2\text{kpsi}$.

Substitute $2819\text{lbf}\cdot \text{in}$ for $T$ and $1.25\text{in}$ for $d$ in Equation (XXVI).

    $\begin{array}{c}\tau =\frac{16\times 2819\text{lbf}\cdot \text{in}}{\pi {\left(1.25\text{in}\right)}^3}\\ =\frac{45104\text{lbf}\cdot \text{in}}{\pi {\left(1.25\text{in}\right)}^3}\\ =\left(7350.809\text{psi}\right)\left(\frac{1\text{kpsi}}{{10}^3\text{psi}}\right)\\ \approx 7.35\text{kpsi}\end{array}$

Thus, the shear stress at point of maximum bending moment is $7.35\text{kpsi}$.

To determine

The principal stresses at point of maximum bending moment.

The maximum shear stress at point of maximum bending moment.

Answer to Problem 72P

The principal stresses at point of maximum bending moment are $36.7\text{kpsi}$ and $-1.47\text{kpsi}$.

The maximum shear stress at point of maximum bending moment is $19.1\text{kpsi}$.

Explanation of Solution

Calculate the maximum principal stress.

    ${\sigma }_1=\frac{\sigma }{2}+\sqrt{{\left(\frac{\sigma }{2}\right)}^2+{\tau }^2}$ (XXVII)

Here, the maximum principal stress is ${\sigma }_1$.

Calculate the minimum principal stress.

    ${\sigma }_2=\frac{\sigma }{2}-\sqrt{{\left(\frac{\sigma }{2}\right)}^2+{\tau }^2}$ (XXVIII)

Here, the minimum principal stress is ${\sigma }_2$.

Calculate the maximum shear stress.

    ${\tau }_{\max }=\sqrt{{\left(\frac{\sigma }{2}\right)}^2+{\tau }^2}$ (XXIX)

Here, maximum shear stress is ${\tau }_{\max }$.

Conclusion:

Substitute $35.2\text{kpsi}$ for $\sigma$ and $7.35\text{kpsi}$ for $\tau$ in Equation (XXVII).

    $\begin{array}{c}{\sigma }_1=\frac{35.2\text{kpsi}}{2}+\sqrt{{\left(\frac{35.2\text{kpsi}}{2}\right)}^2+{\left(7.35\text{kpsi}\right)}^2}\\ =17.6\text{kpsi}+19.07\text{kpsi}\\ \text{=36}\text{.67}\text{kpsi}\\ \approx 36.7\text{kpsi}\end{array}$

Substitute $35.2\text{kpsi}$ for $\sigma$ and $7.35\text{kpsi}$ for $\tau$ n Equation (XXVIII).

    $\begin{array}{c}{\sigma }_2=\frac{35.2\text{kpsi}}{2}-\sqrt{{\left(\frac{35.2\text{kpsi}}{2}\right)}^2+{\left(7.35\text{kpsi}\right)}^2}\\ =17.6\text{kpsi}-19.07\text{kpsi}\\ =-1.47\text{kpsi}\end{array}$

Thus, the principal stresses at the point of maximum bending moment are $36.7\text{kpsi}$ and $-1.47\text{kpsi}$.

Substitute $21.5\text{kpsi}$ for $\sigma$ and $5.09\text{kpsi}$ for $\tau$ in Equation (XXIX).

    $\begin{array}{c}{\tau }_{\max }=\sqrt{{\left(\frac{35.2\text{kpsi}}{2}\right)}^2+{\left(7.35\text{kpsi}\right)}^2}\\ =19.07\text{kpsi}\\ \approx 19.1\text{kpsi}\end{array}$

Thus, the maximum shear stress at point of maximum bending moment is $19.1\text{kpsi}$.