
For each section illustrated, find the second moment of area, the location of the neutral axis, and the distances from the neutral axis to the top and bottom surfaces. Consider that the section is transmitting a positive bending moment about the z axis. Mz, where Mz = 10 kip · in if the dimensions of the section are given in ips units, or Mz = 1.13 kN · m if the dimensions are in SI units. Determine the resulting stresses at the top and bottom surfaces and at every abrupt change in the cross section.
Problem 3–34
(a) 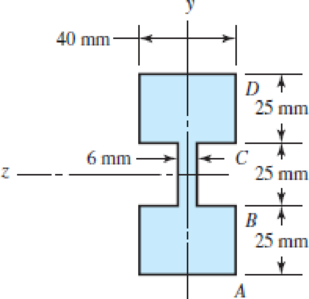
(b) 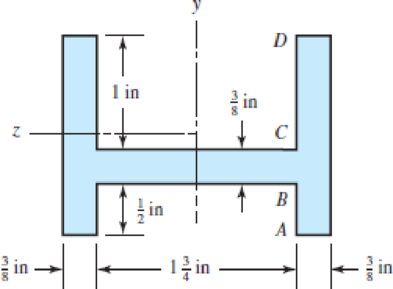
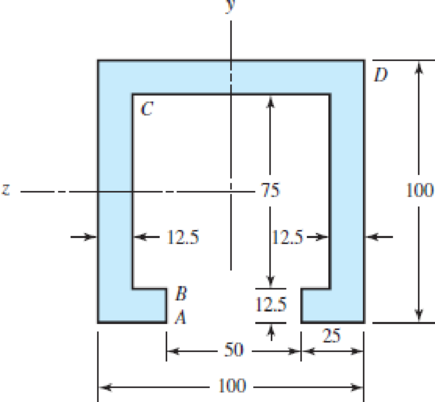
(c) Dimensions in mm
(d) 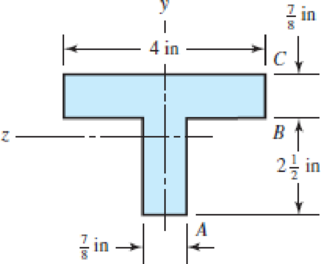
(a)
The second moment of area of the section.
The distance from the neutral axis to the top surfaces.
The distance from the neutral axis to the bottom surfaces.
The resulting stress at the top surface.
The resulting stress at the bottom surface.
The resulting stress at the abrupt change in cross-section.
Answer to Problem 34P
The second moment of area of the section is
The distance from the neutral axis to the top surface is
The distance from the neutral axis to the bottom surface is
The resulting stress at the top surface is
The resulting stress at the bottom surface is
The resulting stress at the abrupt change in cross-section is
Explanation of Solution
Figure-(1) shows two different sections divided of the in the same diagram.
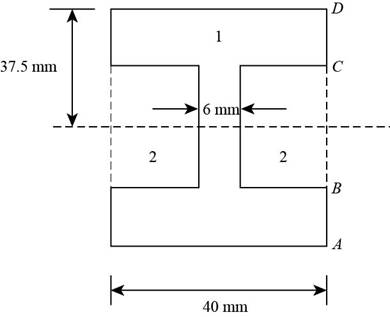
Figure-(1)
Calculate the second moment of area of the section.
Here, the second moment area of the area
Write the moment of inertia of the rectangular section.
Calculate the location of the neutral axis.
Calculate the location of the neutral axis.
Here, the area of the each section is
Write the resulting bending stress on beam.
Here, the distance from the neutral axis to the top or bottom surface is
Conclusion:
Substitute
Substitute
Substitute
Thus, the second moment of area of the section is
Substitute
Since the section is symmetrical about
Thus, the distance from the neutral axis to the top surface is
Thus, the distance from the neutral axis to the bottom surface is
Substitute
Since top and bottom surfaces are at the same distance from the neutral axis so the resulting stresses are same.
Thus, the resulting stress at the top surface is
Thus, the resulting stress at the bottom surface is
Substitute
Thus the resulting stress at the abrupt change in cross-section is
(b)
The second moment of area of the section.
The distance from the neutral axis to the top surface.
The distance from the neutral axis to the bottom surface.
The resulting stress at the point A.
The resulting stress at the point D.
The resulting stress at the abrupt change in cross-section at a point B.
The resulting stress at the abrupt change in cross-section at a point C.
Answer to Problem 34P
The second moment of area of the section is
The distance from the neutral axis to the top surface is
The distance from the neutral axis to the bottom surface is
The resulting stress at the point A is
The resulting stress at the point C is
The resulting stress at the abrupt change in cross-section at a point B is
The resulting stress at the abrupt change in cross-section at a point C is
Explanation of Solution
Figure-(2) shows two different sections divided of the in the same diagram.
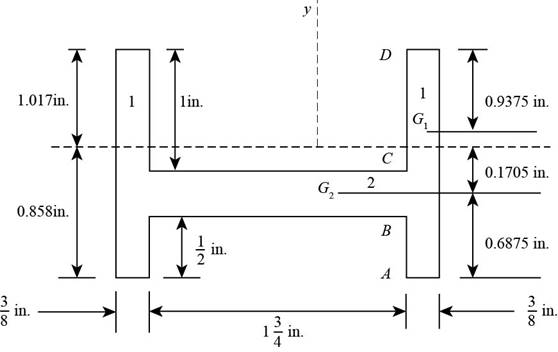
Figure-(2)
Write the expression for the area of section 1.
Here, the width of the section 1 is
Write the expression for the area of section 2.
Here, the width of the section 2 is
Calculate the location of the neutral axis.
Calculate the location of the neutral axis.
Here, the area of the each section is
Write the expression for the moment of inertia of section 1.
Write the expression for the moment of inertia of section 2.
Write the expression for the total moment of inertia.
Here, the distance of the neutral axis from the centroid of section 1 is
Write the resulting bending stress on beam.
Here, the distance from the neutral axis to the top or bottom surface is
Conclusion:
Substitute
Substitute
Substitute
Substitute
Substitute
Since the section is symmetrical about
Thus, the distance from the neutral axis to the top surface is
Thus, the distance from the neutral axis to the bottom surface is
Substitute
Substitute
Distance of the neutral axis from the two different centroids is
Substitute
Thus, the second moment of area of the section is
Substitute
Thus, the resulting stress at the bottom surface at a point A is
Substitute
Thus, the resulting stress at the point B is
Substitute
Thus, the resulting stress at the a point C is
Substitute
Thus, the resulting stress at the a point D is
(c)
The second moment of area of the section.
The distance from the neutral axis to the top surface.
The distance from the neutral axis to the bottom surface.
The resulting stress at the point A.
The resulting stress at the point D.
The resulting stress at the abrupt change in cross-section at a point B.
The resulting stress at the abrupt change in cross-section at a point C.
Answer to Problem 34P
The second moment of area of the section is
The distance from the neutral axis to the top surface is
The distance from the neutral axis to the bottom surface is
The resulting stress at the point A is
The resulting stress at the point D is
The resulting stress at the abrupt change in cross-section at a point B is
The resulting stress at the abrupt change in cross-section at a point C is
Explanation of Solution
Figure-(3) shows three different sections divided of the section in the same diagram.
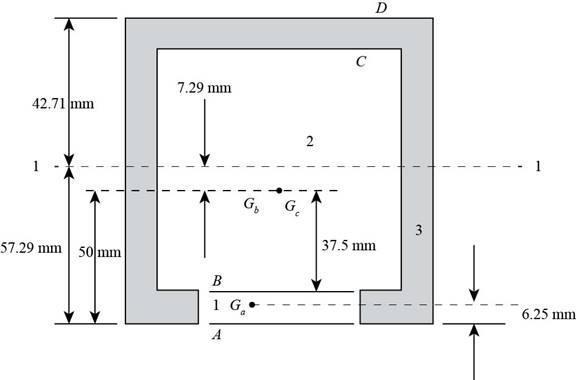
Figure-(3)
Write the expression for the area of section 1.
Here, the width of the section 1 is
Write the expression for the area of section 2.
Here, the width of the section 2 is
Write the expression for the area of section 3.
Here, the width of the section 3 is
Calculate the location of the neutral axis.
Calculate the location of the neutral axis.
Here, the area of the each section is
Write the expression for the moment of inertia of section 1.
Write the expression for the moment of inertia of section 2.
Write the expression for the moment of inertia of section 3.
Write the expression for the total moment of inertia.
Here, the distance of the neutral axis from the centroid of section 1 is
Write the resulting bending stress on beam.
Here, the distance from the neutral axis to the top or bottom surface is
Conclusion:
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Since the section is symmetrical about
Thus, the distance from the neutral axis to the top surface is
Thus, the distance from the neutral axis to the bottom surface is
Substitute
Substitute
Substitute
Distance of the neutral axis from the three different centroids of section is
Substitute
Thus, the second moment of area of the section is
Substitute
Thus, the resulting stress at the bottom surface at a point A is
Substitute
Thus, the resulting stress at the point B is
Substitute
Thus, the resulting stress at the a point C is
Substitute
Thus, the resulting stress at the a point D is
(d)
The second moment of area of the section.
The distance from the neutral axis to the top surface.
The distance from the neutral axis to the bottom surface.
The resulting stress at the point A.
The resulting stress at the point D.
The resulting stress at the abrupt change in cross-section at a point B.
Answer to Problem 34P
The second moment of area of the section is
The distance from the neutral axis to the top surface is
The distance from the neutral axis to the bottom surface is
The resulting stress at the point A is
The resulting stress at the point C is
The resulting stress at the abrupt change in cross-section at a point B is
Explanation of Solution
Figure-(4) shows two different sections divided of the section shown in the same diagram.
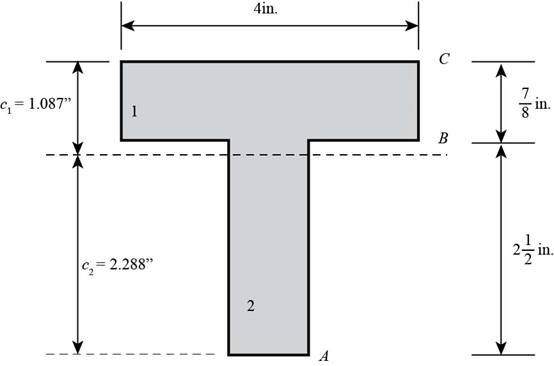
Figure-(4)
Write the expression for the area of section 1.
Here, the width of the section 1 is
Write the expression for the area of section 2.
Here, the width of the section 2 is
Calculate the location of the neutral axis.
Calculate the location of the neutral axis.
Here, the area of the each section is
Write the expression for the moment of inertia of section 1.
Write the expression for the moment of inertia of section 2.
Write the expression for the total moment of inertia.
Here, the distance of the neutral axis from the centroid of section 1 is
Write the resulting bending stress on beam.
Here, the distance from the neutral axis to the top or bottom surface is
Conclusion:
Substitute
Substitute
Substitute
Substitute
Substitute
Since the section is symmetrical about
Thus, the distance from the neutral axis to the top surface is
Thus, the distance from the neutral axis to the bottom surface is
Substitute
Substitute
Distance of the neutral axis from the two different centroids is
Substitute
Thus, the second moment of area of the section is
Substitute
Thus, the resulting stress at the bottom surface at a point A is
Substitute
Thus, the resulting stress at the point B is
Substitute
Thus, the resulting stress at the a point C is
Want to see more full solutions like this?
Chapter 3 Solutions
Shigley's Mechanical Engineering Design (McGraw-Hill Series in Mechanical Engineering)
Additional Engineering Textbook Solutions
Experiencing MIS
Problem Solving with C++ (10th Edition)
Mechanics of Materials (10th Edition)
Fluid Mechanics: Fundamentals and Applications
Vector Mechanics for Engineers: Statics and Dynamics
Thermodynamics: An Engineering Approach
- I tried this problem and don't know what I did wrong or how else I could approach it can you please help me out?arrow_forwardQ3: An engine produce 750 kW power and uses gaseous C12H26 as a fuel at 25 C; 200% theoretical air is used and air enters at 500 K. The products of combustion leave at 800 K. The heat loss from the engine is 175 kW. Determine the fuel consumption for complete combustion.arrow_forwardQu 5 Determine the carburizing time necessary to achieve a carbon concentration of 0.30 wt% at a position 4 mm into an iron carbon alloy that initially contains 0.10 wt% C. The surface concentration is to be maintained at 0.90 wt% C, and the treatment is to be conducted at 1100°C. Use the data for the diffusion of carbon into y-iron: Do = 2.3 x10-5 m2/s and Qd = 148,000 J/mol. Express your answer in hours to three significant figures. show all work step by step problems formula material sciencearrow_forward
- (Read Question)arrow_forwardIn figure A, the homogeneous rod of constant cross section is attached to unyielding supports. In figure B, a homogeneous bar with a cross-sectional area of 600 mm2 is attached to rigid supports. The bar carries the axial loads P1 = 20 kN and P2 = 60 kN, as shown.1. In figure A, derive the expression that calculates the reaction R1 in terms of P, and the given dimensions.2. In figure B, calculate the reaction (kN) at A.3. In figure B, calculate the maximum axial stress (MPa) in the rod.arrow_forward(Read image)arrow_forward
- (Read Image)arrow_forwardM16x2 grade 8.8 bolts No. 25 C1- Q.2. The figure is a cross section of a grade 25 cast-iron pressure vessel. A total of N, M16x2.0 grade 8.8 bolts are to be used to resist a separating force of 160 kN. (a) Determine ks, km, and C. (b) Find the number of bolts required for a load factor of 2 where the bolts may be reused when the joint 19 mm is taken apart. (c) with the number of bolts obtained in (b), determine the realized load factor for overload, the yielding factor of safety, and the separation factor of safety. 19 mmarrow_forwardProblem4. The thin uniform disk of mass m = 1-kg and radius R = 0.1m spins about the bent shaft OG with the angular speed w2 = 20 rad/s. At the same time, the shaft rotates about the z-axis with the angular speed 001 = 10 rad/s. The angle between the bent portion of the shaft and the z-axis is ẞ = 35°. The mass of the shaft is negligible compared to the mass of the disk. a. Find the angular momentum of the disk with respect to point G, based on the axis orientation as shown. Include an MVD in your solution. b. Find the angular momentum of the disk with respect to point O, based on the axis orientation as shown. (Note: O is NOT the center of fixed-point rotation.) c. Find the kinetic energy of the assembly. z R R 002 2R x Answer: H = -0.046ĵ-0.040 kg-m²/sec Ho=-0.146-0.015 kg-m²/sec T 0.518 N-m =arrow_forward
- Problem 3. The assembly shown consists of a solid sphere of mass m and the uniform slender rod of the same mass, both of which are welded to the shaft. The assembly is rotating with angular velocity w at a particular moment. Find the angular momentum with respect to point O, in terms of the axes shown. Answer: Ñ。 = ½mc²wcosßsinßĵ + (}{mr²w + 2mb²w + ½ mc²wcos²ß) k 3 m r b 2 C لا marrow_forwardOnly question 2arrow_forwardOnly question 1arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





