Chapter 3, Problem 74P

(a)

To determine

The free body diagram of the shaft.

The reactions at $C$ and $D$.

Answer to Problem 74P

The free body-diagram of the shaft is as follows.

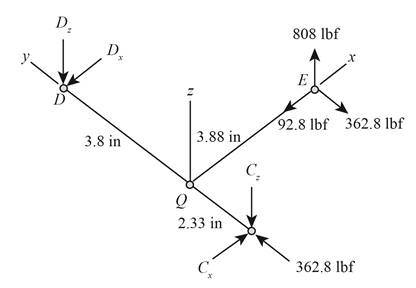
The reaction at $C$ in $x\text{-}$ direction is $287.2\text{lbf}$, the reaction at $C$ in $y\text{-}$ direction is $362.8\text{lbf}$, the reaction at $C$ in $z\text{-}$ direction is $500.9\text{lbf}$, the reaction at $D$ in $x\text{-}$ direction is $194.4\text{lbf}$ and the reaction at $D$ in $z\text{-}$ direction is $307.1\text{lbf}$.

Explanation of Solution

The figure below shows the arrangement of shafts.

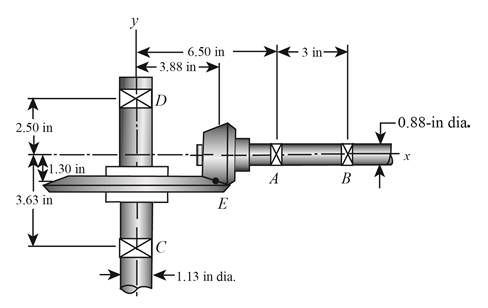
Figure (1)

The free body diagram of the arrangement of shafts is as follows.

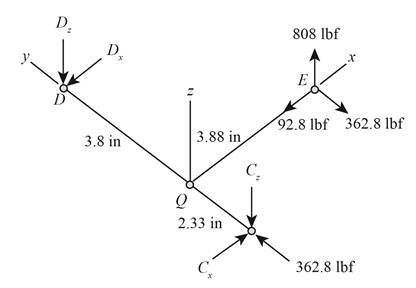
Figure (2)

Write the expression of moment at $D$ in $z\text{-}$ direction.

    $\begin{array}{c}{\displaystyle \sum {\left(M_{D1}\right)}_z}=0\\ \left[\begin{array}{l}\left(l_{DQ}+l_{QC}\right)C_x+\left(l_{DQ}\times {\left(F_x\right)}_E\right)\\ +\left(d_E\times {\left(F_y\right)}_E\right)\end{array}\right]=0\\ C_x=\frac{-\left(l_{DQ}\times {\left(F_x\right)}_E\right)-\left(d_E\times {\left(F_y\right)}_E\right)}{\left(l_{DQ}+l_{QC}\right)}\end{array}$                  (I)

Here, the reaction at $C$ in $x\text{-}$ direction is $C_x$, the length of the shaft $DQ$ is $l_{DQ}$, the length of the shaft $QC$ is $l_{QC}$, the component of force at $E$ in $x\text{-}$ direction is ${\left(F_x\right)}_E$, the component of force at $E$  in $y\text{-}$ direction is ${\left(F_y\right)}_E$ and the diameter of Bevel gear at $E$ is $d_E$.

Write the expression of moment at $C$ in $z\text{-}$ direction.

    $\begin{array}{c}{\displaystyle \sum {\left(M_C\right)}_z}=0\\ \left[\begin{array}{l}\left(l_{DQ}+l_{QC}\right)D_x-\left(l_{QC}\times {\left(F_x\right)}_E\right)\\ +\left(d_E\times {\left(F_y\right)}_E\right)\end{array}\right]=0\\ D_x=\frac{\left(l_{QC}\times {\left(F_x\right)}_E\right)-\left(d_E\times {\left(F_y\right)}_E\right)}{\left(l_{DQ}+l_{QC}\right)}\end{array}$                (II)

Here, the reaction at $D$ in $x\text{-}$ direction is $D_x$.

Write the expression of moment at $D$ in $x\text{-}$ direction.

    $\begin{array}{c}{\left({\displaystyle \sum M_D}\right)}_x=0\\ \left(l_{DQ}+l_{QC}\right)C_z-\left(l_{DQ}\times {\left(F_z\right)}_E\right)=0\\ C_z=\frac{\left(l_{DQ}\times {\left(F_z\right)}_E\right)}{\left(l_{DQ}+l_{QC}\right)}\end{array}$                                              (III)

Here, the reaction at $C$ in $z\text{-}$ direction is $C_z$.

Write the expression of moment at $C$ in $x\text{-}$ direction.

    $\begin{array}{c}{\left({\displaystyle \sum M_C}\right)}_x=0\\ \left(l_{DQ}+l_{QC}\right)D_z-\left(l_{QC}\times {\left(F_z\right)}_E\right)=0\\ D_z=\frac{\left(l_{QC}\times {\left(F_z\right)}_E\right)}{\left(l_{DQ}+l_{QC}\right)}\end{array}$                                            (IV)

Write the expression of net force at $C$ in $y\text{-}$ direction.

    $\begin{array}{c}{C}_y+{\left(F_y\right)}_E=0\\ C_y=-{\left(F_y\right)}_E\end{array}$                                                                                    (V)

Here, the reaction at $C$ in $y\text{-}$ direction is $C_y$.

Conclusion:

Substitute $-92.8\text{lbf}$ for ${\left(F_x\right)}_E$, $3.8\text{in}$ for $l_{DQ}$, $-362.8\text{lbf}$ for ${\left(F_y\right)}_E$, $2.33\text{in}$ for $l_{QC}$ and $3.88\text{in}$ for $d_E$ in Equation (I).

    $\begin{array}{c}{C}_x=\frac{\left(\left(3.8\text{in}\right)\left(-92.8\text{lbf}\right)\right)-\left(\left(3.88\text{in}\right)\left(-362.8\text{lbf}\right)\right)}{\left(3.8\text{in}+2.33\text{in}\right)}\\ =\frac{1055.024\text{lbf}\cdot \text{in}}{6.13\text{in}}\\ =287.16\text{lbf}\\ \approx 287.2\text{lbf}\end{array}$

Thus, the reaction at $C$ in $x\text{-}$ direction is $287.2\text{lbf}$.

Substitute $-92.8\text{lbf}$ for ${\left(F_x\right)}_E$, $3.8\text{in}$ for $l_{DQ}$, $-362.8\text{lbf}$ for ${\left(F_y\right)}_E$, $2.33\text{in}$ for $l_{QC}$ and $3.88\text{in}$ for $d_E$ in Equation (II).

    $\begin{array}{c}{D}_x=\frac{\left(\left(2.33\text{in}\right)\left(-92.8\text{lbf}\right)\right)-\left(\left(3.88\text{in}\right)\left(-362.8\text{lbf}\right)\right)}{\left(\left(3.8\text{in}\right)+\left(2.33\text{in}\right)\right)}\\ =\frac{1191.44\text{lbf}\cdot \text{in}}{6.13\text{in}}\\ \approx 194.4\text{lbf}\end{array}$

Thus, the reaction at $D$ in $x\text{-}$ direction is $194.4\text{lbf}$.

Substitute $808\text{lbf}$ for ${\left(F_z\right)}_E$, $3.8\text{in}$ for $l_{DQ}$ and $2.33\text{in}$ for $l_{QC}$ in Equation (III).

    $\begin{array}{c}{C}_z=\frac{\left(3.8\times 808\right)}{\left(3.8+2.33\right)}\\ =500.88\text{lbf}\\ \approx 500.9\text{lbf}\end{array}$

Thus, the reaction at $C$ in $z\text{-}$ direction is $500.9\text{lbf}$.

Substitute $808\text{lbf}$ for ${\left(F_z\right)}_E$, $3.8\text{in}$ for $l_{DQ}$ and $2.33\text{in}$ for $l_{QC}$ in Equation (IV).

    $\begin{array}{c}{D}_z=\frac{\left(\left(2.33\text{in}\right)\left(808\text{lbf}\right)\right)}{\left(\left(3.8\text{in}\right)+\left(2.33\text{in}\right)\right)}\\ =\frac{1882.64\text{lbf}\cdot \text{in}}{6.13\text{in}}\\ =307.11\text{lbf}\\ \approx 307.1\text{lbf}\end{array}$

Thus, the reaction at $D$ in $z\text{-}$ direction is $307.1\text{lbf}$.

Substitute $-362.8\text{lbf}$ for ${\left(F_y\right)}_E$ in Equation (V).

    $C_y=362.8\text{lbf}$

Thus, the reaction at $C$ in $y\text{-}$ direction is $362.8\text{lbf}$.

(b)

To determine

The shear force and bending moment diagrams.

Answer to Problem 74P

The figure below shows the shear force and bending moment diagram in $x\text{-}$ direction and bending moment diagram in $z\text{-}$ direction.

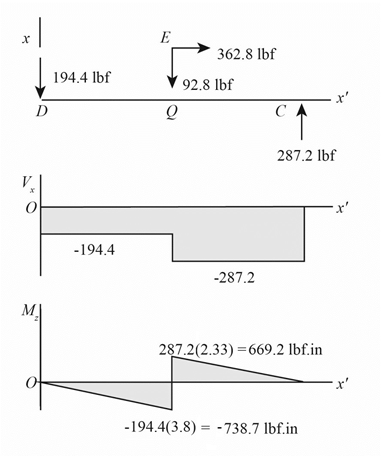
The figure below shows the shear force and bending moment diagram in $z\text{-}$ direction and bending moment diagram in $x\text{-}$ direction.

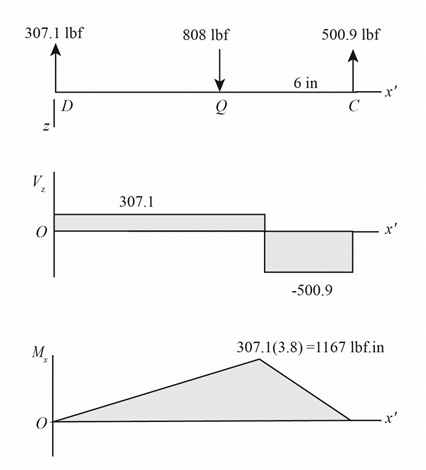
Explanation of Solution

It is clear from the free body diagram of the shaft $DC$ in Figure (2), that the distance are measured in $y\text{-}$ direction and the reactions are measured in $x\text{-}$ direction and $z\text{-}$ direction. Therefore, the shear force diagram and the bending moment diagram for the shaft $DC$ are made in $x\text{-}$ direction and $z\text{-}$ direction only.

The calculations for shear force diagram in $x\text{-}$ direction on shaft $DC$.

Write the expression of Shear force at $D$ in $x\text{-}$ direction.

    $S{F}_{Dx}=-D_x$                                                                                                 (VI)

Here, the shear at $D$ in $x\text{-}$ direction is $S{F}_{Dx}$.

Write the expression of Shear force at $Q$ in $x\text{-}$ direction.

    $S{F}_{Qx}=S{F}_{Dx}+{\left(F_x\right)}_E$                                                                                  (VII)

Here, the shear force at $Q$ in $x\text{-}$ direction is $S{F}_{Qx}$.

Write the expression of Shear force at $C$ in $x\text{-}$ direction.

    $S{F}_{Cx}=S{F}_{Qx}+C_x$                                                                                       (VIII)

Here, the shear force at $C$ in $x\text{-}$ direction is $S{F}_{Cx}$.

The calculations for bending moment diagram in $z\text{-}$ direction on shaft $DC$.

We known that, the bending moment at the supports of the simply supported beam is zero.

Write the bending moment at $D$ and $C$ in $z\text{-}$ direction.

    $M_{Cz}=M_{Dz}=0$

Here, the bending moment at $D$ in $z\text{-}$ direction is $M_{Dz}$ and the bending moment at $C$ in $z\text{-}$ direction is $M_{Cz}$.

Write the expression of bending moment at $Q$ in $z\text{-}$ direction due to shear force at $D$.

    $M_{Qz1}=S{F}_{Dx}\times l_{DQ}$                                                                                        (IX)

Here, the bending moment at $Q$ in $z\text{-}$ direction due to shear force at $D$ is $M_{Qz1}$.

Write the expression of bending moment at $Q$ in $z\text{-}$ direction due to shear force at $C$.

    $M_{Qz2}=C_x\times l_{QC}$                                                                                          (X)

Here, the bending moment at $Q$ in $z\text{-}$ direction due to shear force at $C$ is $M_{Qz2}$.

The calculations for shear force diagram in $z\text{-}$ direction on shaft $DC$.

Write the expression of Shear force at $D$ in $z\text{-}$ direction.

    $S{F}_{Dz}=D_z$                                                                                                    (XI)

Here, the shear at $D$ in $z\text{-}$ direction is $S{F}_{Dz}$.

Write the expression of Shear force at $Q$ in $z\text{-}$ direction.

    $S{F}_{Qz}=S{F}_{Dz}-{\left(F_z\right)}_E$                                                                                  (XII)

Here, the shear force at $Q$ in $z\text{-}$ direction is $S{F}_{Qz}$.

Write the expression of Shear force at $C$ in $z\text{-}$ direction.

    $S{F}_{Cz}=S{F}_{Qz}+C_z$                                                                                      (XIII)

Here, the shear force at $C$ in $z\text{-}$ direction is $S{F}_{Cz}$.

We known that, the bending moment at the supports of the simply supported beam is zero.

Write the bending moment at $D$ and $C$ in $x\text{-}$ direction.

    $M_{Cx}=M_{Dx}=0$

Here, the bending moment at $D$ in $x\text{-}$ direction is $M_{Dx}$ and the bending moment at $C$ in $x\text{-}$ direction is $M_{Cx}$.

Write the expression of bending moment at $Q$ in $x\text{-}$ direction due to shear force at $D$.

    $M_{Qx1}=S{F}_{Dz}\times l_{DQ}$                                                                                     (XIV)

Here, the bending moment at $Q$ in $x\text{-}$ direction due to shear force at $D$ is $M_{Qx1}$.

Conclusion:

Substitute $194.4\text{lbf}$ for $D_x$ in Equation (VI).

    $S{F}_{Dx}=-194.4\text{lbf}$

Substitute $-194.4\text{lbf}$ for $S{F}_{Dx}$ and $-92.8\text{lbf}$ for ${\left(F_x\right)}_E$ in Equation (VII).

    $\begin{array}{c}S{F}_{Qx}=-194.4\text{lbf}-92.8\text{lbf}\\ =-287.2\text{lbf}\end{array}$

Substitute $-287.2\text{lbf}$ for $S{F}_{Qx}$ and $287.2\text{lbf}$ for $C_x$ in Equation (VIII).

    $\begin{array}{c}S{F}_{Cx}=-287.2\text{lbf}+287.2\text{lbf}\\ =0\text{lbf}\end{array}$

Substitute $-194.4\text{lbf}$ for $M_{Qz1}$ and $3.8\text{in}$ for $l_{DQ}$ in Equation (IX).

    $\begin{array}{c}{M}_{Qz1}=\left(-194.4\text{lbf}\right)\left(3.8\text{in}\right)\\ =--738.72\text{lbf}\cdot \text{in}\\ \approx -738.7\text{lbf}\cdot \text{in}\end{array}$

Substitute $287.2\text{lbf}$ for $C_x$ and $2.33\text{in}$ for $l_{QC}$ in Equation (X).

    $\begin{array}{c}{M}_{Qz2}=\left(287.2\text{lbf}\right)\left(2.33\text{in}\right)\\ =669.2\text{lbf}\cdot \text{in}\end{array}$

The figure below shows the shear force and bending moment diagram in $x\text{-}$ direction and bending moment diagram in $z\text{-}$ direction.

Figure (3)

Substitute $307.1\text{lbf}$ for $D_z$ in Equation (XI).

    $S{F}_{Dz}=307.1\text{lbf}$

Substitute $307.1\text{lbf}$ for $S{F}_{Dz}$ and $808\text{lbf}$ for ${\left(F_z\right)}_E$ in Equation (XII).

    $\begin{array}{c}S{F}_{Qz}=307.1\text{lbf}-808\text{lbf}\\ =-500.9\text{lbf}\end{array}$

Substitute $-500.9\text{lbf}$ for $S{F}_{Qz}$ and $500.9\text{lbf}$ for $C_z$ in Equation (XIII).

    $\begin{array}{c}S{F}_{Cz}=-500.9+500.9\\ =0\text{lbf}\end{array}$

Substitute $307.1\text{lbf}$ for $S{F}_{Dz}$ and $3.8\text{in}$ for $l_{DQ}$ in Equation (XIV).

    $\begin{array}{c}{M}_{Qx1}=\left(307.1\text{lbf}\right)\left(3.8\text{in}\right)\\ =1166.98\text{lbf}\cdot \text{in}\\ \approx 1167\text{lbf}\cdot \text{in}\end{array}$

The figure below shows the shear force and bending moment diagram in $z\text{-}$ direction and bending moment diagram in $x\text{-}$ direction.

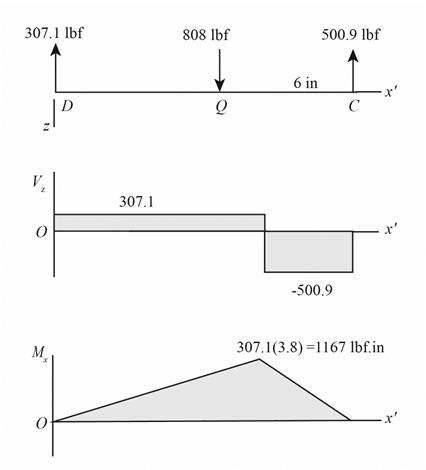
Figure (4)

(c)

To determine

The torsional shear stress for critical stress element.

The bending stress for critical stress element.

The axial stress for critical stress element.

Answer to Problem 74P

The torsional shear stress for critical stress element is $11065.5\text{psi}$.

The bending stress for critical stress element is $\pm 9495\text{psi}$.

The axial stress for critical stress element is $-362\text{psi}$.

Explanation of Solution

It is clear from the bending moment diagram that the critical stress element is located at just right of $Q$, where the bending moment is maximum in both the directions and where torsional and shear stress exists.

Write the expression of maximum torque acting on the shaft $DC$.

    $T={\left(F_z\right)}_E\times d_E$                                                                                           (XV)

Here, the maximum torque acting on the shaft $DC$ is $T$.

Write the expression of maximum bending moment acting on the shaft $DC$.

    $M=\sqrt{{\left(M_{Qz2}\right)}^2+{\left(M_{Qx1}\right)}^2}$                                                                       (XVI)

Here, the maximum bending moment acting on the shaft $DC$ is $M$.

Write the expression of torsional shear stress for critical stress element.

    $\tau =\frac{16T}{\pi d^3}$                                                                                                  (XVII)

Here, the torsional shear stress for critical stress element is $\tau$ and diameter of the shaft is $d$.

Write the expression of bending stress for critical stress element.

    ${\sigma }_b=\pm \frac{32M}{\pi d^3}$                                                                                         (XVIII)

Here, the bending stress for critical stress element is ${\sigma }_b$.

Write the expression of axial stress for critical stress element.

    ${\sigma }_a=-\frac{4F}{\pi d^2}$                                                                                              (XIX)

Here, the axial stress for critical stress element is ${\sigma }_a$.

Conclusion:

Substitute $808\text{lbf}$ for ${\left(F_z\right)}_E$ and $3.88\text{in}$ for $d_E$ in Equation (XV).

    $\begin{array}{c}T=\left(808\text{lbf}\right)\left(3.88\text{in}\right)\\ =3135.04\text{lbf}\cdot \text{in}\\ \approx 3135\text{lbf}\cdot \text{in}\end{array}$

Substitute $699.2\text{lbf}\cdot \text{in}$ for $M_{Qz2}$ and $1167\text{lbf}\cdot \text{in}$ for $M_{Qz1}$ in Equation (XVI).

    $\begin{array}{c}M=\sqrt{{\left(699.2\text{lbf}\cdot \text{in}\right)}^2+{\left(1167\text{lbf}\cdot \text{in}\right)}^2}\\ =\sqrt{1850769.64{\text{lbf}}^2\cdot {\text{in}}^2}\\ =1345.2\text{lbf}\cdot \text{in}\\ \approx 1345\text{lbf}\cdot \text{in}\end{array}$

Substitute $3135\text{lbf}\cdot \text{in}$ for $T$ and $1.13\text{in}$ for $d$ in Equation (XVII).

    $\begin{array}{c}\tau =\frac{16\times \left(3135\text{lbf}\cdot \text{in}\right)}{\pi {\left(1.13\text{in}\right)}^3}\\ =11065.5\text{psi}\end{array}$

Thus, the torsional shear stress for critical stress element is $11065.5\text{psi}$.

Substitute $1345\text{lbf}\cdot \text{in}$ for $M$ and $1.13\text{in}$ for $d$ in Equation (XVIII).

    $\begin{array}{c}{\sigma }_b=\pm \frac{32\times \left(1345\text{lbf}\cdot \text{in}\right)}{\pi \times {\left(1.13\text{in}\right)}^3}\\ =\pm 9494.8\text{psi}\\ \approx \pm 9495\text{psi}\end{array}$

Thus, the bending stress for critical stress element is $\pm 9495\text{psi}$.

Substitute $362.8\text{lbf}$ for $F$ and $1.13\text{in}$ for $d$ in Equation (XIX).

    $\begin{array}{c}{\sigma }_a=-\frac{4\times \left(362.8\text{lbf}\right)}{\pi {\left(1.13\text{in}\right)}^2}\\ =-361.7\text{psi}\\ \approx -362\text{psi}\end{array}$

Thus, the axial stress for critical stress element is $-362\text{psi}$.

(d)

To determine

The principal stresses for critical stress element.

The maximum shear stress for critical stress element.

Answer to Problem 74P

The principal stresses for critical stress element are $7184.94\text{psi}$ and $-17041.94\text{psi}$ respectively.

The maximum shear stress for critical stress element is $12113.44\text{psi}$.

Explanation of Solution

Write the expression of maximum bending stress on the critical stress element.

    ${\sigma }_{\max }=-{\sigma }_b+{\sigma }_a$                                                                                        (XX)

Here, the maximum bending stress on the critical stress element is ${\sigma }_{\max }$.

Write the expression of principal stresses on the critical stress element.

    ${\sigma }_1,{\sigma }_2=\frac{{\sigma }_{\max }}{2}\pm \sqrt{{\left(\frac{{\sigma }_{\max }}{2}\right)}^2+{\tau }^2}$                                                               (XXI)

Here, the principal stresses on the critical stress element are ${\sigma }_1$ and ${\sigma }_2$.

Write the expression of maximum shear stress on the critical stress element.

    ${\sigma }_1,{\sigma }_2=\frac{{\sigma }_{\max }}{2}\pm \sqrt{{\left(\frac{{\sigma }_{\max }}{2}\right)}^2+{\tau }^2}$                                                              (XXII)

Here, the maximum shear stress on the critical stress element is ${\tau }_{\max }$.

Conclusion:

Substitute $9495\text{psi}$ for ${\sigma }_b$ and $-362\text{psi}$ for ${\sigma }_a$ in Equation (XX).

    $\begin{array}{c}{\sigma }_{\max }=-\left(9495\text{psi}\right)+\left(-362\text{psi}\right)\\ =-9857\text{psi}\end{array}$

Substitute $-9857\text{psi}$ for ${\sigma }_{\max }$ and $11065.5\text{psi}$ for $\tau$ in Equation (XXI).

    $\begin{array}{c}{\sigma }_1,{\sigma }_2=\frac{\left(-9857\text{psi}\right)}{2}\pm \sqrt{{\left(\frac{-9857\text{psi}}{2}\right)}^2+{\left(11065.5\text{psi}\right)}^2}\\ =-\left(4928.5\text{psi}\right)\pm \left(12113.44\text{psi}\right)\\ {\sigma }_1=7184.94\text{psi}\\ {\sigma }_2=-17041.94\text{psi}\end{array}$

Thus, the principal stresses for critical stress element are $7184.94\text{psi}$ and $-17041.94\text{psi}$ respectively.

Substitute $-9857\text{psi}$ for ${\sigma }_{\max }$ and $11065.5\text{psi}$ for $\tau$ in Equation (XXII).

    $\begin{array}{c}{\tau }_{\max }=\sqrt{{\left(\frac{\left(-9857\text{psi}\right)}{2}\right)}^2+{\left(11065.5\text{psi}\right)}^2}\\ =\sqrt{14673540.25{\text{psi}}^2}\\ =12113.44\text{psi}\end{array}$

Thus, the maximum shear stress for critical stress element is $12113.44\text{psi}$.