Chapter 3, Problem 71P

A countershaft carrying two V-belt pulleys is shown in the figure. Pulley A receives power from a motor through a belt with the belt tensions shown. The power is transmitted through the shaft and delivered to the belt on pulley B. Assume the belt tension on the loose side at B is 15 percent of the tension on the Light side.

(a) Determine the tensions in the belt on pulley B, assuming the shaft is running at a constant speed.

(b) Find the magnitudes of the bearing reaction forces, assuming the bearings act as simple supports.

(c) Draw shear-force and bending-moment diagrams for the shaft. If needed, make one set for the horizontal plane and another set for the vertical plane.

(d) At the point of maximum bending moment, determine the bending stress and the torsional shear stress.

(e) At the point of maximum bending moment, determine the principal stresses and the maximum shear stress.

Problem 3–71*

Dimensions in millimeters.

To determine

The tensions in the belt on pulley $B$.

Answer to Problem 71P

The tension in the belt pulley $B$ at tight side is $250\text{N}$ and at loose side is $37.5\text{N}$.

Explanation of Solution

Write the relationship between tension on the loose side with respect to tension on the tight side.

    $T_2=0.15T_1$ (I)

Here, the tension on the tight side is $T_1$ and the tension on the loose side is $T_2$.

Write the equation to balance the tension on the counter shaft.

    $\begin{array}{c}{\displaystyle \sum T}=0\\ \left(T_{A1}-T_{A2}\right)\frac{d_A}{2}-\left(T_2-T_1\right)\frac{d_B}{2}=0\end{array}$ (II)

Substitute $0.15T_1$ for $T_2$ in Equation (II).

    $\begin{array}{l}\left(T_{A1}-T_{A2}\right)\frac{d_A}{2}+\left(0.15T_1-T_1\right)\frac{d_B}{2}=0\\ T_1=\frac{1}{0.85}\left(\left(T_{A1}-T_{A2}\right)\frac{d_A}{d_B}\right)\end{array}$ (III)

Here, the tension on the tight side of pulley $A$ is $T_{A1}$, the tension on the loose side of pulley $A$ is $T_{A2}$, diameter of shaft $A$ is $d_A$, and the diameter of shaft $B$ is $d_B$.

Conclusion:

Substitute $300\text{N}$ for $T_{A1}$, $45\text{N}$ for $T_{A2}$, $250\text{mm}$ for $d_A$ and $300\text{mm}$ for $d_B$ in Equation (III).

    $\begin{array}{c}{T}_1=\left(\frac{1}{0.85}\right)\left(300\text{N}-45\text{N}\right)\left(\frac{250\text{mm}}{300\text{mm}}\right)\\ =\left(\frac{1}{0.85}\right)\left(255\text{N}\right)\left(\frac{5\text{mm}}{6\text{mm}}\right)\\ =250\text{N}\end{array}$

Substitute $250\text{N}$ for $T_1$ in Equation (I)

    $\begin{array}{c}{T}_2=0.15\times 250\text{N}\\ =37.5\text{N}\end{array}$

Thus, the tension in the belt pulley $B$ at tight side is $250\text{N}$ and at loose side is $37.5\text{N}$.

To determine

The magnitude of the bearing reaction forces.

Answer to Problem 71P

The magnitude of bearing reaction force at $C$ is $173.56\text{N}$ and at $O$ is $190.85\text{N}$.

Explanation of Solution

Write the expression for magnitude of bearing reaction force at $C$ in $z\text{-}$ direction.

    $\begin{array}{l}{\displaystyle \sum M_{Oy}}=0\\ \left[\left(T_{A1}+T_{A2}\right)\sin \theta \left(l_{OA}\right)-\left(T_1+T_2\right)\left(l_{OA}+l_{AB}\right)-R_{Cz}\left(l_{OA}+l_{AB}+l_{BC}\right)\right]=0\\ R_{Cz}=\frac{\left[\left(T_{A1}+T_{A2}\right)\sin \theta \left(l_{OA}\right)-\left(T_1+T_2\right)\left(l_{OA}+l_{AB}\right)\right]}{\left(l_{OA}+l_{AB}+l_{BC}\right)}\end{array}$ (IV)

Here, the tension on tight side of pulley $A$ is $T_{A1}$, the tension on the loose side of pulley $A$ is $T_{A2}$, the magnitude of the bearing force at $C$ in $z\text{-}$ direction is $R_{Cz}$, distance between $O$ and $A$ is $l_{OA}$, distance between $A$ and $B$ is $l_{AB}$, distance between $B$ and $C$ is $l_{BC}$, and the angle between the tension on the pulley $A$ and $B$ is $\theta$.

Write the expression for magnitude of bearing reaction force at $O$ in $z$-direction.

    $\begin{array}{l}{\displaystyle \sum F_z}=0\\ \left[R_{Oz}-\left(T_{A1}+T_{A2}\right)\cos \theta +\left(T_1+T_2\right)+R_{Cz}\right]=0\\ R_{Oz}=\left(T_{A1}+T_{A2}\right)\cos \theta -\left(T_1+T_2\right)-R_{Cz}\end{array}$ (V)

Write the expression for magnitude of bearing reaction force at $C$ in $y$ direction.

    $\begin{array}{l}{\displaystyle \sum M_{Oz}}=0\\ R_{Cy}\left(l_{OA}+l_{AB}+l_{BC}\right)+\left(T_{A1}+T_{A2}\right)\sin \theta \left(l_{OA}\right)=0\\ R_{Cy}=-\frac{\left(T_{A1}+T_{A2}\right)\sin \theta \left(l_{OA}\right)}{\left(l_{OA}+l_{AB}+l_{BC}\right)}\end{array}$ (VI)

Here, the magnitude of bearing force at $C$ in $y$-direction is $R_{Cy}$.

Write the expression for magnitude of bearing force at $O$ in $y$ direction.

    $\begin{array}{l}{\displaystyle \sum F_y}=0\\ R_{Oy}+\left(T_{A1}+T_{A2}\right)\cos \theta +R_{Cy}=0\\ R_{Oy}=-\left(T_{A1}+T_{A2}\right)\cos \theta -R_{Cy}\end{array}$ (VII)

Here, the magnitude of bearing reaction force at $O$ in $z$ direction is $R_{Oz}$.

Calculate the bearing reaction force at $B$.

    $R_C=\sqrt{R_{Cy}^2+R_{Cz}^2}$ (VIII)

Here, the bearing reaction force at $C$ is $R_C$.

Calculate the bearing reaction force at $O$.

    $R_O=\sqrt{R_{Oy}^2+R_{Oz}^2}$ (IX)

Here, the bearing reaction force at $O$ is $R_O$.

Conclusion:

Substitute $300\text{N}$ for $T_{A1}$, $45\text{N}$ for $T_{A2}$, $250\text{N}$ for $T_1$, $37.5\text{N}$ for $T_2$, $300\text{mm}$ for $l_{OA}$, $400\text{mm}$ for $l_{AB}$, $150\text{mm}$ for $l_{BC}$ and $45°$ for $\theta$ Equation (IV).

    $\begin{array}{c}{R}_{Cz}=\frac{\left\{\begin{array}{l}\left(\left(300\text{N}+45\text{N}\right)\sin 45°\times 300\text{mm}\right)\\ -\left(\left(250\text{N}+37.5\text{N}\right)\left(300\text{mm}+400\text{mm}\right)\right)\end{array}\right\}}{\left(300\text{mm}+400\text{mm}+150\text{mm}\right)}\\ =\frac{\left(345\text{N}\times \frac{1}{\sqrt{2}}\times 300\text{mm}\right)-\left(\left(287.5\text{N}\right)\left(700\text{mm}\right)\right)}{\left(850\text{mm}\right)}\\ =\frac{\left(73185.55\text{N}\cdot \text{mm}\right)-\left(201250\text{N}\cdot \text{mm}\right)}{\left(850\text{mm}\right)}\\ =-150.7\text{N}\end{array}$

Substitute $300\text{N}$ for $T_{A1}$, $45\text{N}$ for $T_{A2}$, $250\text{N}$ for $T_1$, $37.5\text{N}$ for $T_2$, $45°$ for $\theta$ and $-150.7\text{N}$ for $R_{Cz}$ in Equation (V).

    $\begin{array}{c}{R}_{Oz}=\left(300\text{N}+45\text{N}\right)\cos 45°-\left(250\text{N}+37.5\text{N}\right)+150.7\text{N}\\ \text{=}\left(345\text{N}\right)\left(\frac{1}{\sqrt{2}}\right)-\left(287.5\text{N}\right)+\left(150.7\text{N}\right)\\ =\text{243}\text{.95}\text{N}-136.8\text{N}\\ \approx 107.2\text{N}\end{array}$

Substitute $300\text{N}$ for $T_{A1}$, $45\text{N}$ for $T_{A2}$, $300\text{mm}$ for $l_{OA}$, $400\text{mm}$ for $l_{AB}$, $150\text{mm}$ for $l_{BC}$ and $45°$ for $\theta$ in Equation (VI.)

    $\begin{array}{c}{R}_{Cy}=-\frac{\left(300\text{N}+45\text{N}\right)\left(\sin 45°\right)\left(300\text{mm}\right)}{\left(300\text{mm}+400\text{mm}+150\text{mm}\right)}\\ =-\frac{\left(345\text{N}\right)\left(\frac{1}{\sqrt{2}}\right)\left(300\text{mm}\right)}{\left(850\text{mm}\right)}\\ =-\frac{\left(73185.55\text{N}\cdot \text{mm}\right)}{\left(850\text{mm}\right)}\\ \approx -86.10\text{N}\end{array}$

Substitute $300\text{N}$ for $T_{A1}$, $45\text{N}$ for $T_{A2}$, $-86.10\text{N}$ for $R_{Cy}$ and $45°$ for $\theta$ in Equation (VII)

    $\begin{array}{c}{R}_{Oy}=-\left(300\text{N}+45\text{N}\right)\cos 45°+86.10\text{N}\\ =-\left(345\text{N}\right)\left(\frac{1}{\sqrt{2}}\right)+86.10\text{N}\\ \text{=}-243.95\text{N}+86.10\text{N}\\ \approx -157.9\text{N}\end{array}$

Substitute $-150.7\text{N}$ for $R_{Cz}$ and $-86.1\text{N}$ for $R_{Cy}$ in Equation (VIII)

    $\begin{array}{c}{R}_C=\sqrt{{\left(-150.7\text{N}\right)}^2+{\left(-86.1\text{N}\right)}^2}\\ =\sqrt{\left(22710.49{\text{N}}^2\right)+\left(7413.21{\text{N}}^2\right)}\\ =\sqrt{\left(30123.7{\text{N}}^2\right)}\\ =173.56\text{N}\end{array}$

Substitute $-157.9\text{N}$ for $R_{Oy}$ and $107.2\text{N}$ for $R_{Oz}$ in Equation (IX).

    $\begin{array}{c}{R}_O=\sqrt{{\left(-157.9\text{N}\right)}^2+{\left(107.2\text{N}\right)}^2}\\ =\sqrt{\left(24932.41{\text{N}}^2\right)+\left(11491.84{\text{N}}^2\right)}\\ =\sqrt{\left(36424.25{\text{N}}^2\right)}\\ =190.85\text{N}\end{array}$

Thus, the magnitude of bearing reaction force at $C$ is $173.56\text{N}$ and at $O$ is $190.85\text{N}$.

To determine

The shear force diagram and bending moment diagram for the shaft.

Answer to Problem 71P

The shear force diagram and bending moment diagram for the shaft in $y\text{-}$ direction is as follows.

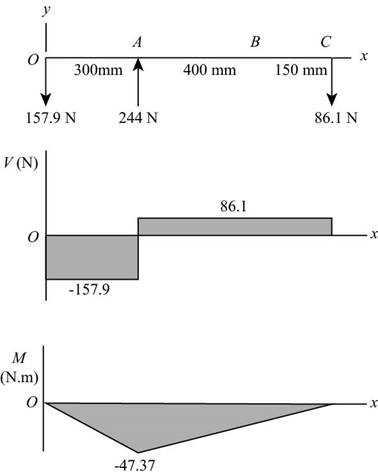
The shear force diagram and bending moment diagram for the shaft in $z\text{-}$ direction is as follows.

Explanation of Solution

The calculations for shear force and bending moment diagram in $y$-direction.

Calculate the shear force at $O$ in $y$-direction.

    $S{F}_{Oy}=R_{Oy}$ (X)

Here, the shear force at $O$ in $y\text{-}$ direction is $S{F}_{Oy}$.

Calculate the shear force at $A$ in $y$-direction.

    $S{F}_{Ay}=S{F}_{Oy}+(T_{A1}+T_{A2})\cos \theta$ (XI)

Here, the shear force at $A$ in $y$ direction is $S{F}_{Ay}$.

Calculate the shear force at $C$ in $y$-direction.

    $S{F}_{Cy}=S{F}_{Ay}+R_{Cy}$ (XII)

Here, the shear force at $C$ in $y$ direction is $S{F}_{Cy}$.

Calculate the moment at $O$ and $C$.

    $M_O=M_C=0$ (XIII)

The moment at the supports of the simply supported beam is zero.

Calculate the moment at $A$ in $y$-direction.

    $M_{Ay}=S{F}_{Oy}\times l_{OA}$ (XIV)

Here, the moment at $A$ is $M_A$ in $y$-direction.

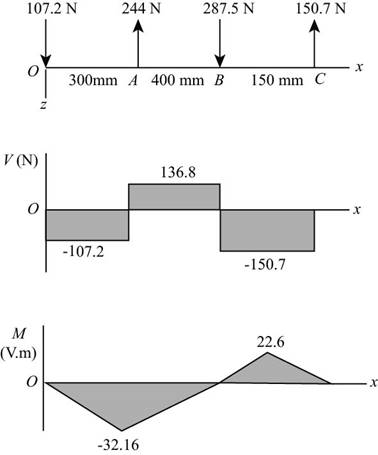
The calculations for shear force and bending moment diagram in $z\text{-}$ direction.

Calculate the shear force at $O$ in $z$-direction.

    $S{F}_{Oz}=-R_{Oz}$ (XV)

Here, the shear force at $O$ in $z$-direction is $S{F}_{Oz}$.

Calculate the shear force at $A$ in $z$-direction.

    $S{F}_{Az}=S{F}_{Oz}+\left(T_{A1}+T_{A2}\right)\sin 45°$ (XVI)

Here, the shear force at $A$ in $z$-direction is $S{F}_{Az}$.

Calculate the shear force at $B$ in $z$-direction.

    $S{F}_{Bz}=S{F}_{Az}-\left(T_1+T_2\right)$ (XVII)

Calculate the shear force at $C$ in $z$-direction.

    $S{F}_{Cz}=S{F}_{Bz}-R_{Cz}$ (XVIII)

Here, the shear force at $C$ in $z$-direction is $S{F}_{Cz}$.

Calculate the moment at $O$ and $C$.

    $M_O=M_C=0$ (XIX)

The moment at the supports of the simply supported beam is zero.

Calculate the moment at $A$ in $z$-direction.

    $M_{Az}=S{F}_{Oz}\times l_{OA}$ (XX)

Here, the moment at $A$ is $M_{Az}$ in $z$-direction.

Calculate the moment at $B$ in $z$-direction.

    $M_{Bz}=-R_{Cz}\times l_{BC}$ (XXI)

Here, the moment at $A$ is $M_{Bz}$ in $z$-direction.

Conclusion:

Substitute $-157.9\text{N}$ for $R_{Oy}$ in Equation (X).

    $S{F}_{Oy}=-157.9\text{N}$

Substitute $-157.9\text{N}$ for $S{F}_{Oy}$, $300\text{N}$ for $T_{A1}$, $45\text{N}$ for $T_{A2}$ and $45°$ for $\theta$ in Equation (XI).

    $\begin{array}{c}S{F}_{Ay}=-157.9\text{N}+(300\text{N}+45\text{N})\cos \left(45°\right)\\ =-157.9\text{N}+(345\text{N})\left(\frac{1}{\sqrt{2}}\right)\\ =\left(-157.9\text{N}\right)+(243.95\text{N})\\ \approx 86.1\text{N}\end{array}$

Substitute $-86.1\text{N}$ for $R_{Cy}$ and $86.1\text{N}$ for $S{F}_A$ in Equation (XII).

    $\begin{array}{c}S{F}_{Cy}=86.1\text{N}-86.1\text{N}\\ =0\text{N}\end{array}$

Substitute $-157.9\text{N}$ for $S{F}_{Oy}$ and $300\text{mm}$ for $l_{OA}$ in Equation (XIV).

    $\begin{array}{c}{M}_{Ay}=\left(-157.9\text{N}\right)\left(300\text{mm}\right)\\ =\left(-157.9\text{N}\right)\left(300\text{mm}\right)\left(\frac{1\text{m}}{1000\text{mm}}\right)\\ =\left(-157.9\text{N}\right)\left(0.3\text{m}\right)\\ =-47.37\text{N}\cdot \text{m}\end{array}$

Thus, the shear force diagram and bending moment diagram for the shaft in $y\text{-}$ direction is as follows.

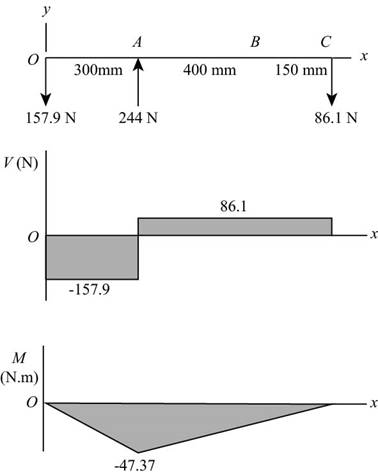
Figure-(1)

Substitute $107.2\text{N}$ for $R_{Oz}$ in Equation (XV).

    $S{F}_{Oz}=-107.2\text{N}$

Substitute $-107.2\text{N}$ for $S{F}_{Oz}$, $300\text{N}$ for $T_{A1}$, $45\text{N}$ for $T_{A2}$ and $45°$ for $\theta$ in Equation (XVI).

    $\begin{array}{c}S{F}_{Az}=-107.2\text{N}+\left(300\text{N}+45\text{N}\right)\cos 45°\\ =-107.2\text{N}+\left(345\text{N}\right)\left(\frac{1}{\sqrt{2}}\right)\\ =-107.2\text{N}+243.95\\ \approx 136.8\text{N}\end{array}$

Substitute $136.8\text{N}$ for $S{F}_{Az}$, $250\text{N}$ for $T_1$ and $37.5\text{N}$ for $T_2$ in Equation (XVII).

    $\begin{array}{c}S{F}_{Bz}=136.8\text{N}-\left(250\text{N}+37.5\text{N}\right)\\ =136.8\text{N}-\left(287.5\text{N}\right)\\ =-150.7\text{N}\end{array}$

Substitute $-150.7$ for $S{F}_{Bz}$ and $-150.7$ for $R_{Cz}$ in Equation (XVIII).

    $\begin{array}{c}S{F}_{Cz}=-150.7\text{N}+150.7\text{N}\\ =0\text{N}\end{array}$

Substitute $-107.2\text{N}$ for $S{F}_{Oz}$ and $300\text{mm}$ for $l_{OA}$ in Equation (XX).

    $\begin{array}{c}{M}_{Az}=\left(-107.2\text{N}\right)\left(300\text{mm}\right)\\ =\left(-107.2\text{N}\right)\left(300\text{mm}\right)\left(\frac{1\text{m}}{1000\text{mm}}\right)\\ =\left(-107.2\text{N}\right)\left(0.3\text{m}\right)\\ =-32.16\text{N}\cdot \text{m}\end{array}$

Substitute $-150.7\text{N}$ for $R_{Cz}$ and $150\text{mm}$ for $l_{BC}$ in Equation (XXI).

    $\begin{array}{c}{M}_{Bz}=-\left(-150.7\text{N}\right)\left(150\text{mm}\right)\\ =-\left(-150.7\text{N}\right)\left(150\text{mm}\right)\left(\frac{1\text{m}}{1000\text{mm}}\right)\\ =\left(150.7\text{N}\right)\left(0.15\text{m}\right)\\ =22.6\text{N}\cdot \text{m}\end{array}$

Thus, the shear force diagram and bending moment diagram for the shaft in $y$ direction is as follows.

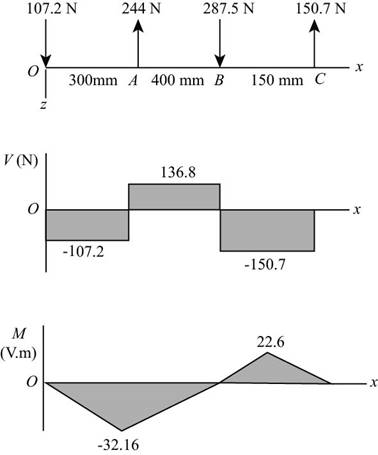
Figure-(2)

To determine

The bending stress at point of maximum bending moment.

The shear stress at point of maximum bending moment.

Answer to Problem 71P

The bending stress at point of maximum bending moment is $72.9\text{MPa}$.

The shear stress at point of maximum bending moment is $20.3\text{MPa}$.

Explanation of Solution

It is clear from the bending moment diagrams, that the critical location is at $A$. At this point, there will be maximum bending moment.

Write the net moment at $A$.

    $M_A=\sqrt{M_{Ay}^2+M_{Az}^2}$ (XXII)

Here, the net moment at $A$ is $M_A$.

Write the torque transmitted by shaft from $A$ to $B$.

    $T=\left(T_{A1}-T_{A2}\right)\times \frac{d_A}{2}$ (XXIII)

Here, the torque transmitted by shaft from $A$ to $B$ is $T$.

Calculate the bending stress.

    $\sigma =\frac{32M_A}{\pi d^3}$ (XXIV)

Here, the bending stress is $\sigma$ and diameter of shaft is $d$.

Calculate the shear stress.

    $\tau =\frac{16T}{\pi d^3}$ (XXV)

Here, the shear stress is $\tau$.

Conclusion:

Substitute $-47.37\text{N}\cdot \text{m}$ for $M_{Ay}$ and $-32.16\text{N}\cdot \text{m}$ for $M_{Az}$ in Equation (XXII).

    $\begin{array}{c}{M}_A=\sqrt{{\left(-47.37\text{N}\cdot \text{m}\right)}^2+{\left(-32.16\text{N}\cdot \text{m}\right)}^2}\\ =\sqrt{\left(2243.91{\text{N}}^2\cdot {\text{m}}^2\right)+\left(1034.26{\text{N}}^2\cdot {\text{m}}^2\right)}\\ =\sqrt{\left(3278.17{\text{N}}^2\cdot {\text{m}}^2\right)}\\ \approx 57.26\text{N}\cdot \text{m}\end{array}$

Substitute $300\text{N}$ for $T_{A1}$, $45\text{N}$ for $T_{A2}$ and $250\text{mm}$ for $d_A$ in Equation (XXIII).

    $\begin{array}{c}T=\left(300\text{N}-45\text{N}\right)\frac{\left(250\text{mm}\right)}{2}\\ =\left(255\text{N}\right)\frac{\left(250\text{mm}\right)}{2}\left(\frac{1\text{m}}{1000\text{mm}}\right)\\ =\left(31875\text{N}\cdot \text{mm}\right)\left(\frac{1\text{m}}{1000\text{mm}}\right)\\ \approx 31.88\text{N}\cdot \text{m}\end{array}$

Convert the diameter of the shaft from $\text{mm}$ to $\text{m}$.

    $\begin{array}{c}d=20\text{mm}\\ =\left(20\text{mm}\right)\left(\frac{1\text{m}}{1000\text{mm}}\right)\\ =0.02\text{m}\end{array}$

Substitute $57.26\text{N}\cdot \text{m}$ for $M_A$ and $0.02\text{m}$ for $d$ in Equation (XXV).

    $\begin{array}{c}\sigma =\frac{32\times 57.26\text{N}\cdot \text{m}}{\pi {\left(0.02\text{m}\right)}^3}\\ =\frac{1832.32\text{N}\cdot \text{m}}{\pi \left(8\times {10}^{-6}{\text{m}}^3\right)}\\ =\left(72.9\times {10}^6\text{Pa}\right)\left(\frac{1\text{MPa}}{{10}^6\text{Pa}}\right)\\ =72.9\text{MPa}\end{array}$

Thus, the bending stress at point of maximum bending moment is $72.9\text{MPa}$.

Substitute $31.88\text{N}\cdot \text{m}$ for $T$ and $0.02\text{m}$ for $d$ in Equation (XXVI).

    $\begin{array}{c}\tau =\frac{16\times 31.88\text{N}\cdot \text{m}}{\pi {\left(0.02\text{m}\right)}^3}\\ =\frac{510.08\text{N}\cdot \text{m}}{\pi \left(8\times {10}^{-6}{\text{m}}^3\right)}\\ =\left(20.29\times {10}^6\text{Pa}\right)\left(\frac{1\text{MPa}}{{10}^6\text{Pa}}\right)\\ \approx 20.3\text{MPa}\end{array}$

Thus, the shear stress at point of maximum bending moment is $20.3\text{MPa}$.

To determine

The principal stresses at point of maximum bending moment.

The maximum shear stress at point of maximum bending moment.

Answer to Problem 71P

The principal stresses at point of maximum bending moment are $78.2\text{MPa}$ and $-5.27\text{MPa}$.

The maximum shear stress at point of maximum bending moment is $41.7\text{MPa}$.

Explanation of Solution

Calculate the maximum principal stress.

    ${\sigma }_1=\frac{\sigma }{2}+\sqrt{{\left(\frac{\sigma }{2}\right)}^2+{\tau }^2}$ (XXVI)

Here, the maximum principal stress is ${\sigma }_1$.

Calculate the minimum principal stress.

    ${\sigma }_2=\frac{\sigma }{2}-\sqrt{{\left(\frac{\sigma }{2}\right)}^2+{\tau }^2}$ (XXVII)

Here, the minimum principal stress is ${\sigma }_2$.

Calculate the maximum shear stress.

    ${\tau }_{\max }=\sqrt{{\left(\frac{\sigma }{2}\right)}^2+{\tau }^2}$ (XXVIII)

Here, maximum shear stress is ${\tau }_{\max }$.

Conclusion:

Substitute $72.9\text{MPa}$ for $\sigma$ and $20.3\text{MPa}$ for $\tau$ in Equation (XXVI).

    $\begin{array}{c}{\sigma }_1=\frac{72.9\text{MPa}}{2}+\sqrt{{\left(\frac{72.9\text{MPa}}{2}\right)}^2+{\left(20.3\text{MPa}\right)}^2}\\ =\frac{72.9\text{MPa}}{2}+\sqrt{\left(1328.60{\text{MPa}}^2\right)+\left(412.09{\text{MPa}}^2\right)}\\ =36.45\text{MPa}+41.72\text{MPa}\\ \approx 78.2\text{MPa}\end{array}$

Substitute $72.9\text{MPa}$ for $\sigma$ and $20.3\text{MPa}$ for $\tau$ in Equation (XXVII).

    $\begin{array}{c}{\sigma }_2=\frac{72.9\text{MPa}}{2}-\sqrt{{\left(\frac{72.9\text{MPa}}{2}\right)}^2+{\left(20.3\text{MPa}\right)}^2}\\ =\frac{72.9\text{MPa}}{2}-\sqrt{\left(1328.60{\text{MPa}}^2\right)+\left(412.09{\text{MPa}}^2\right)}\\ =36.45\text{MPa}-41.7\text{MPa}\\ =-5.25\text{MPa}\end{array}$

The principal stresses at point of maximum bending moment are $78.2\text{MPa}$ and $-5.27\text{MPa}$.

Substitute $72.9\text{MPa}$ for $\sigma$ and $20.3\text{MPa}$ for $\tau$ in Equation (XXVIII).

    $\begin{array}{c}{\tau }_{\max }=\sqrt{{\left(\frac{72.9\text{MPa}}{2}\right)}^2+{\left(20.3\text{MPa}\right)}^2}\\ =\sqrt{\left(1328.60{\text{MPa}}^2\right)+\left(412.09{\text{MPa}}^2\right)}\\ =\sqrt{\left(1740.69{\text{MPa}}^2\right)}\\ \approx 41.7\text{MPa}\end{array}$

Thus, the maximum shear stress at point of maximum bending moment is $41.7\text{MPa}$.