Precalculus with Limits: A Graphing Approach
Precalculus with Limits: A Graphing Approach
7th Edition
ISBN: 9781305071711
Author: Ron Larson
Publisher: Brooks/Cole
bartleby

Concept explainers

Minimization
In mathematics, traditional optimization problems are typically expressed in terms of minimization. When we talk about minimizing or maximizing a function, we refer to the maximum and minimum possible values of that function. This can be expressed in ter…
Maxima and Minima
The extreme points of a function are the maximum and the minimum points of the function. A maximum is attained when the function takes the maximum value and a minimum is attained when the function takes the minimum value.
Derivatives
A derivative means a change. Geometrically it can be represented as a line with some steepness. Imagine climbing a mountain which is very steep and 500 meters high. Is it easier to climb? Definitely not! Suppose walking on the road for 500 meters. Which …
Concavity
In calculus, concavity is a descriptor of mathematics that tells about the shape of the graph. It is the parameter that helps to estimate the maximum and minimum value of any of the functions and the concave nature using the graphical method. We use the …
bartleby

Videos

Question
Book Icon
Chapter 2.2, Problem 109E

a.

To determine

To verify that the volume of the box is given by the function V(x)=x(36−2x)2.

a.

Expert Solution
Check Mark

Answer to Problem 109E

The volume of the box is V(x)=x(36−2x)2, hence verified.

Explanation of Solution

Given:

An open box is to be made from a square piece of material 36 centimeters on a side by cutting equal squares with sides of length x from the corners and turning up the sides.

Concept Used:

Volume of the box= length×width×height.

Calculation:

Length of the box =36- 2x .

Width of the box =36- 2x .

Height of the box = x .

  Volume  of the box=length×width×heigthV(x)=(36−2x)(36−2x)x.V(x)=x(36−2x)2.

Conclusion:

The volume of the box is V(x)=x(36−2x)2 .

b.

To determine

To find the domain of the function V.

b.

Expert Solution
Check Mark

Answer to Problem 109E

The domain of the function V is 0<x <18 cm.

Explanation of Solution

Given:

An open box is to be made from a square piece of material 36 centimeters on a side by cutting equal squares with sides of length x from the corners and turning up the sides.

Calculation:

Need to cut something, so x >0.

But cannot more than half the side length of the material. So also x<362=18

Conclusion:

The domain of the function V is 0<x <18 cm.

c.

To determine

To use the table feature of a graphing utility to create a table that shows various box height x and the corresponding volumes V. Use the table to estimate a range of dimensions within which the maximum volume is produced.

c.

Expert Solution
Check Mark

Answer to Problem 109E

The maximum volume seems to occur between 5 and 7 cm.

Explanation of Solution

Given:

An open box is to be made from a square piece of material 36 centimeters on a side by cutting equal squares with sides of length x from the corners and turning up the sides.

Calculation:

Using graphing utility below table that shows various box height x and the corresponding volumes V as y.

    Height xVolume V
    00.00
    11156.00
    22048.00
    32700
    43136.00
    53380.00
    63456.00
    73388.00
    83200.00
    92916.00
    102560.00
    112156.00
    121728
    131300
    14896.00
    15540.00
    16256.00
    1768.00
    180.00

Conclusion:

The maximum volume seems to occur between 5 and 7 cm.

d.

To determine

To use the graphing utility to graph V and use the range of dimension from part (c ) to find the x −value for which V(x) is maximum.

d.

Expert Solution
Check Mark

Answer to Problem 109E

The maximum occurs at exactly x =6 cm , with volume at 3456 cm3 .

Explanation of Solution

Given:

An open box is to be made from a square piece of material 36 centimeters on a side by cutting equal squares with sides of length x from the corners and turning up the sides.

Calculation:

Using graphing utility below table that shows various box height x and the corresponding volumes V as y.

    Height x cmVolume V cm3
    00.00
    11156.00
    22048.00
    32700
    43136.00
    53380.00
    63456.00
    73388.00
    83200.00
    92916.00
    102560.00
    112156.00
    121728
    131300
    14896.00
    15540.00
    16256.00
    1768.00
    180.00

The Graph on above table is shown below.

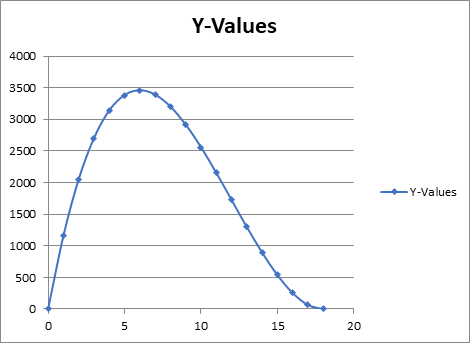
  Precalculus with Limits: A Graphing Approach, Chapter 2.2, Problem 109E

Conclusion:

The maximum occurs at exactly x =6 cm , with volume at 3456 cm3 .

Previous
Chapter 2.2, Problem 108E
Next
Chapter 2.2, Problem 110E

Chapter 2 Solutions

Precalculus with Limits: A Graphing Approach

Ch. 2.1 - Prob. 1ECh. 2.1 - Prob. 2ECh. 2.1 - Prob. 3ECh. 2.1 - Prob. 4ECh. 2.1 - Prob. 5ECh. 2.1 - Prob. 6ECh. 2.1 - Prob. 7ECh. 2.1 - Prob. 8ECh. 2.1 - Prob. 9ECh. 2.1 - Prob. 10E
Ch. 2.1 - Prob. 11ECh. 2.1 - Prob. 12ECh. 2.1 - Prob. 13ECh. 2.1 - Prob. 14ECh. 2.1 - Prob. 15ECh. 2.1 - Prob. 16ECh. 2.1 - Prob. 17ECh. 2.1 - Prob. 18ECh. 2.1 - Prob. 19ECh. 2.1 - Prob. 20ECh. 2.1 - Prob. 21ECh. 2.1 - Prob. 22ECh. 2.1 - Prob. 23ECh. 2.1 - Prob. 24ECh. 2.1 - Prob. 25ECh. 2.1 - Prob. 26ECh. 2.1 - Prob. 27ECh. 2.1 - Prob. 28ECh. 2.1 - Prob. 29ECh. 2.1 - Prob. 30ECh. 2.1 - Prob. 31ECh. 2.1 - Prob. 32ECh. 2.1 - Prob. 33ECh. 2.1 - Prob. 34ECh. 2.1 - Prob. 35ECh. 2.1 - Prob. 36ECh. 2.1 - Prob. 37ECh. 2.1 - Prob. 38ECh. 2.1 - Prob. 39ECh. 2.1 - Prob. 40ECh. 2.1 - Prob. 41ECh. 2.1 - Prob. 42ECh. 2.1 - Prob. 43ECh. 2.1 - Prob. 44ECh. 2.1 - Prob. 45ECh. 2.1 - Prob. 46ECh. 2.1 - Prob. 47ECh. 2.1 - Prob. 48ECh. 2.1 - Prob. 49ECh. 2.1 - Prob. 50ECh. 2.1 - Prob. 51ECh. 2.1 - Prob. 52ECh. 2.1 - Prob. 53ECh. 2.1 - Prob. 54ECh. 2.1 - Prob. 55ECh. 2.1 - Prob. 56ECh. 2.1 - Prob. 57ECh. 2.1 - Prob. 58ECh. 2.1 - Prob. 59ECh. 2.1 - Prob. 60ECh. 2.1 - Prob. 61ECh. 2.1 - Prob. 62ECh. 2.1 - Prob. 63ECh. 2.1 - Prob. 64ECh. 2.1 - Prob. 65ECh. 2.1 - Prob. 66ECh. 2.1 - Prob. 67ECh. 2.1 - Prob. 68ECh. 2.1 - Prob. 69ECh. 2.1 - Prob. 70ECh. 2.1 - Prob. 71ECh. 2.1 - Prob. 72ECh. 2.1 - Prob. 73ECh. 2.1 - Prob. 74ECh. 2.1 - Prob. 75ECh. 2.1 - Prob. 76ECh. 2.1 - Prob. 77ECh. 2.1 - Prob. 78ECh. 2.1 - Prob. 79ECh. 2.1 - Prob. 80ECh. 2.1 - Prob. 81ECh. 2.1 - Prob. 82ECh. 2.1 - Prob. 83ECh. 2.1 - Prob. 84ECh. 2.1 - Prob. 85ECh. 2.1 - Prob. 86ECh. 2.1 - Prob. 87ECh. 2.1 - Prob. 88ECh. 2.1 - Prob. 89ECh. 2.1 - Prob. 90ECh. 2.1 - Prob. 91ECh. 2.1 - Prob. 92ECh. 2.1 - Prob. 93ECh. 2.2 - Prob. 1ECh. 2.2 - Prob. 2ECh. 2.2 - Prob. 3ECh. 2.2 - Prob. 4ECh. 2.2 - Prob. 5ECh. 2.2 - Prob. 6ECh. 2.2 - Prob. 7ECh. 2.2 - Prob. 8ECh. 2.2 - Prob. 9ECh. 2.2 - Prob. 10ECh. 2.2 - Prob. 11ECh. 2.2 - Prob. 12ECh. 2.2 - Prob. 13ECh. 2.2 - Prob. 14ECh. 2.2 - Prob. 15ECh. 2.2 - Prob. 16ECh. 2.2 - Prob. 17ECh. 2.2 - Prob. 18ECh. 2.2 - Prob. 19ECh. 2.2 - Prob. 20ECh. 2.2 - Prob. 21ECh. 2.2 - Prob. 22ECh. 2.2 - Prob. 23ECh. 2.2 - Prob. 24ECh. 2.2 - Prob. 25ECh. 2.2 - Prob. 26ECh. 2.2 - Prob. 27ECh. 2.2 - Prob. 28ECh. 2.2 - Prob. 29ECh. 2.2 - Prob. 30ECh. 2.2 - Prob. 31ECh. 2.2 - Prob. 32ECh. 2.2 - Prob. 33ECh. 2.2 - Prob. 34ECh. 2.2 - Prob. 35ECh. 2.2 - Prob. 36ECh. 2.2 - Prob. 37ECh. 2.2 - Prob. 38ECh. 2.2 - Prob. 39ECh. 2.2 - Prob. 40ECh. 2.2 - Prob. 41ECh. 2.2 - Prob. 42ECh. 2.2 - Prob. 43ECh. 2.2 - Prob. 44ECh. 2.2 - Prob. 45ECh. 2.2 - Prob. 46ECh. 2.2 - Prob. 47ECh. 2.2 - Prob. 48ECh. 2.2 - Prob. 49ECh. 2.2 - Prob. 50ECh. 2.2 - Prob. 51ECh. 2.2 - Prob. 52ECh. 2.2 - Prob. 53ECh. 2.2 - Prob. 54ECh. 2.2 - Prob. 55ECh. 2.2 - Prob. 56ECh. 2.2 - Prob. 57ECh. 2.2 - Prob. 58ECh. 2.2 - Prob. 59ECh. 2.2 - Prob. 60ECh. 2.2 - Prob. 61ECh. 2.2 - Prob. 62ECh. 2.2 - Prob. 63ECh. 2.2 - Prob. 64ECh. 2.2 - Prob. 65ECh. 2.2 - Prob. 66ECh. 2.2 - Prob. 67ECh. 2.2 - Prob. 68ECh. 2.2 - Prob. 69ECh. 2.2 - Prob. 70ECh. 2.2 - Prob. 71ECh. 2.2 - Prob. 72ECh. 2.2 - Prob. 73ECh. 2.2 - Prob. 74ECh. 2.2 - Prob. 75ECh. 2.2 - Prob. 76ECh. 2.2 - Prob. 77ECh. 2.2 - Prob. 78ECh. 2.2 - Prob. 79ECh. 2.2 - Prob. 80ECh. 2.2 - Prob. 81ECh. 2.2 - Prob. 82ECh. 2.2 - Prob. 83ECh. 2.2 - Prob. 84ECh. 2.2 - Prob. 85ECh. 2.2 - Prob. 86ECh. 2.2 - Prob. 87ECh. 2.2 - Prob. 88ECh. 2.2 - Prob. 89ECh. 2.2 - Prob. 90ECh. 2.2 - Prob. 91ECh. 2.2 - Prob. 92ECh. 2.2 - Prob. 93ECh. 2.2 - Prob. 94ECh. 2.2 - Prob. 95ECh. 2.2 - Prob. 96ECh. 2.2 - Prob. 97ECh. 2.2 - Prob. 98ECh. 2.2 - Prob. 99ECh. 2.2 - Prob. 100ECh. 2.2 - Prob. 101ECh. 2.2 - Prob. 102ECh. 2.2 - Prob. 103ECh. 2.2 - Prob. 104ECh. 2.2 - Prob. 105ECh. 2.2 - Prob. 106ECh. 2.2 - Prob. 107ECh. 2.2 - Prob. 108ECh. 2.2 - Prob. 109ECh. 2.2 - Prob. 110ECh. 2.2 - Prob. 111ECh. 2.2 - Prob. 112ECh. 2.2 - Prob. 113ECh. 2.2 - Prob. 114ECh. 2.2 - Prob. 115ECh. 2.2 - Prob. 116ECh. 2.2 - Prob. 117ECh. 2.2 - Prob. 118ECh. 2.2 - Prob. 119ECh. 2.2 - Prob. 120ECh. 2.2 - Prob. 121ECh. 2.2 - Prob. 122ECh. 2.2 - Prob. 123ECh. 2.2 - Prob. 124ECh. 2.2 - Prob. 125ECh. 2.2 - Prob. 126ECh. 2.2 - Prob. 127ECh. 2.2 - Prob. 128ECh. 2.2 - Prob. 129ECh. 2.2 - Prob. 130ECh. 2.2 - Prob. 131ECh. 2.2 - Prob. 132ECh. 2.3 - Prob. 1ECh. 2.3 - Prob. 2ECh. 2.3 - Prob. 3ECh. 2.3 - Prob. 4ECh. 2.3 - Prob. 5ECh. 2.3 - Prob. 6ECh. 2.3 - Prob. 7ECh. 2.3 - Prob. 8ECh. 2.3 - Prob. 9ECh. 2.3 - Prob. 10ECh. 2.3 - Prob. 11ECh. 2.3 - Prob. 12ECh. 2.3 - Prob. 13ECh. 2.3 - Prob. 14ECh. 2.3 - Prob. 15ECh. 2.3 - Prob. 16ECh. 2.3 - Prob. 17ECh. 2.3 - Prob. 18ECh. 2.3 - Prob. 19ECh. 2.3 - Prob. 20ECh. 2.3 - Prob. 21ECh. 2.3 - Prob. 22ECh. 2.3 - Prob. 23ECh. 2.3 - Prob. 24ECh. 2.3 - Prob. 25ECh. 2.3 - Prob. 26ECh. 2.3 - Prob. 27ECh. 2.3 - Prob. 28ECh. 2.3 - Prob. 29ECh. 2.3 - Prob. 30ECh. 2.3 - Prob. 31ECh. 2.3 - Prob. 32ECh. 2.3 - Prob. 33ECh. 2.3 - Prob. 34ECh. 2.3 - Prob. 35ECh. 2.3 - Prob. 36ECh. 2.3 - Prob. 37ECh. 2.3 - Prob. 38ECh. 2.3 - Prob. 39ECh. 2.3 - Prob. 40ECh. 2.3 - Prob. 41ECh. 2.3 - Prob. 42ECh. 2.3 - Prob. 43ECh. 2.3 - Prob. 44ECh. 2.3 - Prob. 45ECh. 2.3 - Prob. 46ECh. 2.3 - Prob. 47ECh. 2.3 - Prob. 48ECh. 2.3 - Prob. 49ECh. 2.3 - Prob. 50ECh. 2.3 - Prob. 51ECh. 2.3 - Prob. 52ECh. 2.3 - Prob. 53ECh. 2.3 - Prob. 54ECh. 2.3 - Prob. 55ECh. 2.3 - Prob. 56ECh. 2.3 - Prob. 57ECh. 2.3 - Prob. 58ECh. 2.3 - Prob. 59ECh. 2.3 - Prob. 60ECh. 2.3 - Prob. 61ECh. 2.3 - Prob. 62ECh. 2.3 - Prob. 63ECh. 2.3 - Prob. 64ECh. 2.3 - Prob. 65ECh. 2.3 - Prob. 66ECh. 2.3 - Prob. 67ECh. 2.3 - Prob. 68ECh. 2.3 - Prob. 69ECh. 2.3 - Prob. 70ECh. 2.3 - Prob. 71ECh. 2.3 - Prob. 72ECh. 2.3 - Prob. 73ECh. 2.3 - Prob. 74ECh. 2.3 - Prob. 75ECh. 2.3 - Prob. 76ECh. 2.3 - Prob. 77ECh. 2.3 - Prob. 78ECh. 2.3 - Prob. 79ECh. 2.3 - Prob. 80ECh. 2.3 - Prob. 81ECh. 2.3 - Prob. 82ECh. 2.3 - Prob. 83ECh. 2.3 - Prob. 84ECh. 2.3 - Prob. 85ECh. 2.3 - Prob. 86ECh. 2.3 - Prob. 87ECh. 2.3 - Prob. 88ECh. 2.3 - Prob. 89ECh. 2.3 - Prob. 90ECh. 2.3 - Prob. 91ECh. 2.3 - Prob. 92ECh. 2.3 - Prob. 93ECh. 2.3 - Prob. 94ECh. 2.3 - Prob. 95ECh. 2.3 - Prob. 96ECh. 2.3 - Prob. 97ECh. 2.3 - Prob. 98ECh. 2.3 - Prob. 99ECh. 2.3 - Prob. 100ECh. 2.3 - Prob. 101ECh. 2.3 - Prob. 102ECh. 2.3 - Prob. 103ECh. 2.3 - Prob. 104ECh. 2.3 - Prob. 105ECh. 2.3 - Prob. 106ECh. 2.3 - Prob. 107ECh. 2.3 - Prob. 108ECh. 2.3 - Prob. 109ECh. 2.3 - Prob. 110ECh. 2.3 - Prob. 111ECh. 2.3 - Prob. 112ECh. 2.3 - Prob. 113ECh. 2.3 - Prob. 114ECh. 2.3 - Prob. 115ECh. 2.3 - Prob. 116ECh. 2.3 - Prob. 117ECh. 2.3 - Prob. 118ECh. 2.3 - Prob. 119ECh. 2.3 - Prob. 120ECh. 2.4 - Prob. 1ECh. 2.4 - Prob. 2ECh. 2.4 - Prob. 3ECh. 2.4 - Prob. 4ECh. 2.4 - Prob. 5ECh. 2.4 - Prob. 6ECh. 2.4 - Prob. 7ECh. 2.4 - Prob. 8ECh. 2.4 - Prob. 9ECh. 2.4 - Prob. 10ECh. 2.4 - Prob. 11ECh. 2.4 - Prob. 12ECh. 2.4 - Prob. 13ECh. 2.4 - Prob. 14ECh. 2.4 - Prob. 15ECh. 2.4 - Prob. 16ECh. 2.4 - Prob. 17ECh. 2.4 - Prob. 18ECh. 2.4 - Prob. 19ECh. 2.4 - Prob. 20ECh. 2.4 - Prob. 21ECh. 2.4 - Prob. 22ECh. 2.4 - Prob. 23ECh. 2.4 - Prob. 24ECh. 2.4 - Prob. 25ECh. 2.4 - Prob. 26ECh. 2.4 - Prob. 27ECh. 2.4 - Prob. 28ECh. 2.4 - Prob. 29ECh. 2.4 - Prob. 30ECh. 2.4 - Prob. 31ECh. 2.4 - Prob. 32ECh. 2.4 - Prob. 33ECh. 2.4 - Prob. 34ECh. 2.4 - Prob. 35ECh. 2.4 - Prob. 36ECh. 2.4 - Prob. 37ECh. 2.4 - Prob. 38ECh. 2.4 - Prob. 39ECh. 2.4 - Prob. 40ECh. 2.4 - Prob. 41ECh. 2.4 - Prob. 42ECh. 2.4 - Prob. 43ECh. 2.4 - Prob. 44ECh. 2.4 - Prob. 45ECh. 2.4 - Prob. 46ECh. 2.4 - Prob. 47ECh. 2.4 - Prob. 48ECh. 2.4 - Prob. 49ECh. 2.4 - Prob. 50ECh. 2.4 - Prob. 51ECh. 2.4 - Prob. 52ECh. 2.4 - Prob. 53ECh. 2.4 - Prob. 54ECh. 2.4 - Prob. 55ECh. 2.4 - Prob. 56ECh. 2.4 - Prob. 57ECh. 2.4 - Prob. 58ECh. 2.4 - Prob. 59ECh. 2.4 - Prob. 60ECh. 2.4 - Prob. 61ECh. 2.4 - Prob. 62ECh. 2.4 - Prob. 63ECh. 2.4 - Prob. 64ECh. 2.4 - Prob. 65ECh. 2.4 - Prob. 66ECh. 2.4 - Prob. 67ECh. 2.4 - Prob. 68ECh. 2.4 - Prob. 69ECh. 2.4 - Prob. 70ECh. 2.4 - Prob. 71ECh. 2.4 - Prob. 72ECh. 2.4 - Prob. 73ECh. 2.4 - Prob. 74ECh. 2.4 - Prob. 75ECh. 2.4 - Prob. 76ECh. 2.4 - Prob. 77ECh. 2.4 - Prob. 78ECh. 2.4 - Prob. 79ECh. 2.4 - Prob. 80ECh. 2.4 - Prob. 81ECh. 2.4 - Prob. 82ECh. 2.4 - Prob. 83ECh. 2.4 - Prob. 84ECh. 2.4 - Prob. 85ECh. 2.4 - Prob. 86ECh. 2.4 - Prob. 87ECh. 2.4 - Prob. 88ECh. 2.4 - Prob. 89ECh. 2.4 - Prob. 90ECh. 2.4 - Prob. 91ECh. 2.4 - Prob. 92ECh. 2.4 - Prob. 93ECh. 2.4 - Prob. 94ECh. 2.4 - Prob. 95ECh. 2.4 - Prob. 96ECh. 2.4 - Prob. 97ECh. 2.4 - Prob. 98ECh. 2.4 - Prob. 99ECh. 2.4 - Prob. 100ECh. 2.5 - Prob. 1ECh. 2.5 - Prob. 2ECh. 2.5 - Prob. 3ECh. 2.5 - Prob. 4ECh. 2.5 - Prob. 5ECh. 2.5 - Prob. 6ECh. 2.5 - Prob. 7ECh. 2.5 - Prob. 8ECh. 2.5 - Prob. 9ECh. 2.5 - Prob. 10ECh. 2.5 - Prob. 11ECh. 2.5 - Prob. 12ECh. 2.5 - Prob. 13ECh. 2.5 - Prob. 14ECh. 2.5 - Prob. 15ECh. 2.5 - Prob. 16ECh. 2.5 - Prob. 17ECh. 2.5 - Prob. 18ECh. 2.5 - Prob. 19ECh. 2.5 - Prob. 20ECh. 2.5 - Prob. 21ECh. 2.5 - Prob. 22ECh. 2.5 - Prob. 23ECh. 2.5 - Prob. 24ECh. 2.5 - Prob. 25ECh. 2.5 - Prob. 26ECh. 2.5 - Prob. 27ECh. 2.5 - Prob. 28ECh. 2.5 - Prob. 29ECh. 2.5 - Prob. 30ECh. 2.5 - Prob. 31ECh. 2.5 - Prob. 32ECh. 2.5 - Prob. 33ECh. 2.5 - Prob. 34ECh. 2.5 - Prob. 35ECh. 2.5 - Prob. 36ECh. 2.5 - Prob. 37ECh. 2.5 - Prob. 38ECh. 2.5 - Prob. 39ECh. 2.5 - Prob. 40ECh. 2.5 - Prob. 41ECh. 2.5 - Prob. 42ECh. 2.5 - Prob. 43ECh. 2.5 - Prob. 44ECh. 2.5 - Prob. 45ECh. 2.5 - Prob. 46ECh. 2.5 - Prob. 47ECh. 2.5 - Prob. 48ECh. 2.5 - Prob. 49ECh. 2.5 - Prob. 50ECh. 2.5 - Prob. 51ECh. 2.5 - Prob. 52ECh. 2.5 - Prob. 53ECh. 2.5 - Prob. 54ECh. 2.5 - Prob. 55ECh. 2.5 - Prob. 56ECh. 2.5 - Prob. 57ECh. 2.5 - Prob. 58ECh. 2.5 - Prob. 59ECh. 2.5 - Prob. 60ECh. 2.5 - Prob. 61ECh. 2.5 - Prob. 62ECh. 2.5 - Prob. 63ECh. 2.5 - Prob. 64ECh. 2.5 - Prob. 65ECh. 2.5 - Prob. 66ECh. 2.5 - Prob. 67ECh. 2.5 - Prob. 68ECh. 2.5 - Prob. 69ECh. 2.5 - Prob. 70ECh. 2.5 - Prob. 71ECh. 2.5 - Prob. 72ECh. 2.5 - Prob. 73ECh. 2.5 - Prob. 74ECh. 2.5 - Prob. 75ECh. 2.5 - Prob. 76ECh. 2.5 - Prob. 77ECh. 2.5 - Prob. 78ECh. 2.6 - Prob. 1ECh. 2.6 - Prob. 2ECh. 2.6 - Prob. 3ECh. 2.6 - Prob. 4ECh. 2.6 - Prob. 5ECh. 2.6 - Prob. 6ECh. 2.6 - Prob. 7ECh. 2.6 - Prob. 8ECh. 2.6 - Prob. 9ECh. 2.6 - Prob. 10ECh. 2.6 - Prob. 11ECh. 2.6 - Prob. 12ECh. 2.6 - Prob. 13ECh. 2.6 - Prob. 14ECh. 2.6 - Prob. 15ECh. 2.6 - Prob. 16ECh. 2.6 - Prob. 17ECh. 2.6 - Prob. 18ECh. 2.6 - Prob. 19ECh. 2.6 - Prob. 20ECh. 2.6 - Prob. 21ECh. 2.6 - Prob. 22ECh. 2.6 - Prob. 23ECh. 2.6 - Prob. 24ECh. 2.6 - Prob. 25ECh. 2.6 - Prob. 26ECh. 2.6 - Prob. 27ECh. 2.6 - Prob. 28ECh. 2.6 - Prob. 29ECh. 2.6 - Prob. 30ECh. 2.6 - Prob. 31ECh. 2.6 - Prob. 32ECh. 2.6 - Prob. 33ECh. 2.6 - Prob. 34ECh. 2.6 - Prob. 35ECh. 2.6 - Prob. 36ECh. 2.6 - Prob. 37ECh. 2.6 - Prob. 38ECh. 2.6 - Prob. 39ECh. 2.6 - Prob. 40ECh. 2.6 - Prob. 41ECh. 2.6 - Prob. 42ECh. 2.6 - Prob. 43ECh. 2.6 - Prob. 44ECh. 2.6 - Prob. 45ECh. 2.6 - Prob. 46ECh. 2.6 - Prob. 47ECh. 2.6 - Prob. 48ECh. 2.6 - Prob. 49ECh. 2.6 - Prob. 50ECh. 2.6 - Prob. 51ECh. 2.6 - Prob. 52ECh. 2.6 - Prob. 53ECh. 2.6 - Prob. 54ECh. 2.6 - Prob. 55ECh. 2.6 - Prob. 56ECh. 2.6 - Prob. 57ECh. 2.6 - Prob. 58ECh. 2.6 - Prob. 59ECh. 2.6 - Prob. 60ECh. 2.6 - Prob. 61ECh. 2.6 - Prob. 62ECh. 2.6 - Prob. 63ECh. 2.6 - Prob. 64ECh. 2.7 - Prob. 1ECh. 2.7 - Prob. 2ECh. 2.7 - Prob. 3ECh. 2.7 - Prob. 4ECh. 2.7 - Prob. 5ECh. 2.7 - Prob. 6ECh. 2.7 - Prob. 7ECh. 2.7 - Prob. 8ECh. 2.7 - Prob. 9ECh. 2.7 - Prob. 10ECh. 2.7 - Prob. 11ECh. 2.7 - Prob. 12ECh. 2.7 - Prob. 13ECh. 2.7 - Prob. 14ECh. 2.7 - Prob. 15ECh. 2.7 - Prob. 16ECh. 2.7 - Prob. 17ECh. 2.7 - Prob. 18ECh. 2.7 - Prob. 19ECh. 2.7 - Prob. 20ECh. 2.7 - Prob. 21ECh. 2.7 - Prob. 22ECh. 2.7 - Prob. 23ECh. 2.7 - Prob. 24ECh. 2.7 - Prob. 25ECh. 2.7 - Prob. 26ECh. 2.7 - Prob. 27ECh. 2.7 - Prob. 28ECh. 2.7 - Prob. 29ECh. 2.7 - Prob. 30ECh. 2.7 - Prob. 31ECh. 2.7 - Prob. 32ECh. 2.7 - Prob. 33ECh. 2.7 - Prob. 34ECh. 2.7 - Prob. 35ECh. 2.7 - Prob. 36ECh. 2.7 - Prob. 37ECh. 2.7 - Prob. 38ECh. 2.7 - Prob. 39ECh. 2.7 - Prob. 40ECh. 2.7 - Prob. 41ECh. 2.7 - Prob. 42ECh. 2.7 - Prob. 43ECh. 2.7 - Prob. 44ECh. 2.7 - Prob. 45ECh. 2.7 - Prob. 46ECh. 2.7 - Prob. 47ECh. 2.7 - Prob. 48ECh. 2.7 - Prob. 49ECh. 2.7 - Prob. 50ECh. 2.7 - Prob. 51ECh. 2.7 - Prob. 52ECh. 2.7 - Prob. 53ECh. 2.7 - Prob. 54ECh. 2.7 - Prob. 55ECh. 2.7 - Prob. 56ECh. 2.7 - Prob. 57ECh. 2.7 - Prob. 58ECh. 2.7 - Prob. 59ECh. 2.7 - Prob. 60ECh. 2.7 - Prob. 61ECh. 2.7 - Prob. 62ECh. 2.7 - Prob. 63ECh. 2.7 - Prob. 64ECh. 2.7 - Prob. 65ECh. 2.7 - Prob. 66ECh. 2.7 - Prob. 67ECh. 2.7 - Prob. 68ECh. 2.7 - Prob. 69ECh. 2.7 - Prob. 70ECh. 2.7 - Prob. 71ECh. 2.7 - Prob. 72ECh. 2.7 - Prob. 73ECh. 2.7 - Prob. 74ECh. 2.7 - Prob. 75ECh. 2.7 - Prob. 76ECh. 2.7 - Prob. 77ECh. 2.7 - Prob. 78ECh. 2.7 - Prob. 79ECh. 2.7 - Prob. 80ECh. 2.7 - Prob. 81ECh. 2.7 - Prob. 82ECh. 2.7 - Prob. 83ECh. 2.7 - Prob. 84ECh. 2.7 - Prob. 85ECh. 2.7 - Prob. 86ECh. 2.7 - Prob. 87ECh. 2.7 - Prob. 88ECh. 2.7 - Prob. 89ECh. 2.7 - Prob. 90ECh. 2.7 - Prob. 91ECh. 2.7 - Prob. 92ECh. 2.7 - Prob. 93ECh. 2.7 - Prob. 94ECh. 2.7 - Prob. 95ECh. 2.7 - Prob. 96ECh. 2.7 - Prob. 97ECh. 2.7 - Prob. 98ECh. 2.7 - Prob. 99ECh. 2.7 - Prob. 100ECh. 2.7 - Prob. 101ECh. 2.7 - Prob. 102ECh. 2.7 - Prob. 103ECh. 2.7 - Prob. 104ECh. 2.7 - Prob. 105ECh. 2.7 - Prob. 106ECh. 2.7 - Prob. 107ECh. 2.8 - Prob. 1ECh. 2.8 - Prob. 2ECh. 2.8 - Prob. 3ECh. 2.8 - Prob. 4ECh. 2.8 - Prob. 5ECh. 2.8 - Prob. 6ECh. 2.8 - Prob. 7ECh. 2.8 - Prob. 8ECh. 2.8 - Prob. 9ECh. 2.8 - Prob. 10ECh. 2.8 - Prob. 11ECh. 2.8 - Prob. 12ECh. 2.8 - Prob. 13ECh. 2.8 - Prob. 14ECh. 2.8 - Prob. 15ECh. 2.8 - Prob. 16ECh. 2.8 - Prob. 17ECh. 2.8 - Prob. 18ECh. 2.8 - Prob. 19ECh. 2.8 - Prob. 20ECh. 2.8 - Prob. 21ECh. 2.8 - Prob. 22ECh. 2.8 - Prob. 23ECh. 2.8 - Prob. 24ECh. 2.8 - Prob. 25ECh. 2.8 - Prob. 26ECh. 2.8 - Prob. 27ECh. 2.8 - Prob. 28ECh. 2.8 - Prob. 29ECh. 2.8 - Prob. 30ECh. 2.8 - Prob. 31ECh. 2.8 - Prob. 32ECh. 2.8 - Prob. 33ECh. 2.8 - Prob. 34ECh. 2.8 - Prob. 35ECh. 2.8 - Prob. 36ECh. 2.8 - Prob. 37ECh. 2.8 - Prob. 38ECh. 2 - Prob. 1RECh. 2 - Prob. 2RECh. 2 - Prob. 3RECh. 2 - Prob. 4RECh. 2 - Prob. 5RECh. 2 - Prob. 6RECh. 2 - Prob. 7RECh. 2 - Prob. 8RECh. 2 - Prob. 9RECh. 2 - Prob. 10RECh. 2 - Prob. 11RECh. 2 - Prob. 12RECh. 2 - Prob. 13RECh. 2 - Prob. 14RECh. 2 - Prob. 15RECh. 2 - Prob. 16RECh. 2 - Prob. 17RECh. 2 - Prob. 18RECh. 2 - Prob. 19RECh. 2 - Prob. 20RECh. 2 - Prob. 21RECh. 2 - Prob. 22RECh. 2 - Prob. 23RECh. 2 - Prob. 24RECh. 2 - Prob. 25RECh. 2 - Prob. 26RECh. 2 - Prob. 27RECh. 2 - Prob. 28RECh. 2 - Prob. 29RECh. 2 - Prob. 30RECh. 2 - Prob. 31RECh. 2 - Prob. 32RECh. 2 - Prob. 33RECh. 2 - Prob. 34RECh. 2 - Prob. 35RECh. 2 - Prob. 36RECh. 2 - Prob. 37RECh. 2 - Prob. 38RECh. 2 - Prob. 39RECh. 2 - Prob. 40RECh. 2 - Prob. 41RECh. 2 - Prob. 42RECh. 2 - Prob. 43RECh. 2 - Prob. 44RECh. 2 - Prob. 45RECh. 2 - Prob. 46RECh. 2 - Prob. 47RECh. 2 - Prob. 48RECh. 2 - Prob. 49RECh. 2 - Prob. 50RECh. 2 - Prob. 51RECh. 2 - Prob. 52RECh. 2 - Prob. 53RECh. 2 - Prob. 54RECh. 2 - Prob. 55RECh. 2 - Prob. 56RECh. 2 - Prob. 57RECh. 2 - Prob. 58RECh. 2 - Prob. 59RECh. 2 - Prob. 60RECh. 2 - Prob. 61RECh. 2 - Prob. 62RECh. 2 - Prob. 63RECh. 2 - Prob. 64RECh. 2 - Prob. 65RECh. 2 - Prob. 66RECh. 2 - Prob. 67RECh. 2 - Prob. 68RECh. 2 - Prob. 69RECh. 2 - Prob. 70RECh. 2 - Prob. 71RECh. 2 - Prob. 72RECh. 2 - Prob. 73RECh. 2 - Prob. 74RECh. 2 - Prob. 75RECh. 2 - Prob. 76RECh. 2 - Prob. 77RECh. 2 - Prob. 78RECh. 2 - Prob. 79RECh. 2 - Prob. 80RECh. 2 - Prob. 81RECh. 2 - Prob. 82RECh. 2 - Prob. 83RECh. 2 - Prob. 84RECh. 2 - Prob. 85RECh. 2 - Prob. 86RECh. 2 - Prob. 87RECh. 2 - Prob. 88RECh. 2 - Prob. 89RECh. 2 - Prob. 90RECh. 2 - Prob. 91RECh. 2 - Prob. 92RECh. 2 - Prob. 93RECh. 2 - Prob. 94RECh. 2 - Prob. 95RECh. 2 - Prob. 96RECh. 2 - Prob. 97RECh. 2 - Prob. 98RECh. 2 - Prob. 99RECh. 2 - Prob. 100RECh. 2 - Prob. 101RECh. 2 - Prob. 102RECh. 2 - Prob. 103RECh. 2 - Prob. 104RECh. 2 - Prob. 105RECh. 2 - Prob. 106RECh. 2 - Prob. 107RECh. 2 - Prob. 108RECh. 2 - Prob. 109RECh. 2 - Prob. 110RECh. 2 - Prob. 111RECh. 2 - Prob. 112RECh. 2 - Prob. 113RECh. 2 - Prob. 114RECh. 2 - Prob. 115RECh. 2 - Prob. 116RECh. 2 - Prob. 117RECh. 2 - Prob. 118RECh. 2 - Prob. 119RECh. 2 - Prob. 120RECh. 2 - Prob. 121RECh. 2 - Prob. 122RECh. 2 - Prob. 123RECh. 2 - Prob. 124RECh. 2 - Prob. 125RECh. 2 - Prob. 126RECh. 2 - Prob. 127RECh. 2 - Prob. 128RECh. 2 - Prob. 129RECh. 2 - Prob. 130RECh. 2 - Prob. 131RECh. 2 - Prob. 132RECh. 2 - Prob. 133RECh. 2 - Prob. 134RECh. 2 - Prob. 135RECh. 2 - Prob. 136RECh. 2 - Prob. 137RECh. 2 - Prob. 138RECh. 2 - Prob. 139RECh. 2 - Prob. 140RECh. 2 - Prob. 141RECh. 2 - Prob. 142RECh. 2 - Prob. 143RECh. 2 - Prob. 144RECh. 2 - Prob. 145RECh. 2 - Prob. 146RECh. 2 - Prob. 147RECh. 2 - Prob. 148RECh. 2 - Prob. 149RECh. 2 - Prob. 150RECh. 2 - Prob. 151RECh. 2 - Prob. 152RECh. 2 - Prob. 153RECh. 2 - Prob. 154RECh. 2 - Prob. 155RECh. 2 - Prob. 156RECh. 2 - Prob. 157RECh. 2 - Prob. 158RECh. 2 - Prob. 159RECh. 2 - Prob. 160RECh. 2 - Prob. 161RECh. 2 - Prob. 162RECh. 2 - Prob. 163RECh. 2 - Prob. 164RECh. 2 - Prob. 165RECh. 2 - Prob. 166RECh. 2 - Prob. 167RECh. 2 - Prob. 168RECh. 2 - Prob. 1CTCh. 2 - Prob. 2CTCh. 2 - Prob. 3CTCh. 2 - Prob. 4CTCh. 2 - Prob. 5CTCh. 2 - Prob. 6CTCh. 2 - Prob. 7CTCh. 2 - Prob. 8CTCh. 2 - Prob. 9CTCh. 2 - Prob. 10CTCh. 2 - Prob. 11CTCh. 2 - Prob. 12CTCh. 2 - Prob. 13CTCh. 2 - Prob. 14CTCh. 2 - Prob. 15CTCh. 2 - Prob. 16CTCh. 2 - Prob. 17CTCh. 2 - Prob. 18CTCh. 2 - Prob. 19CTCh. 2 - Prob. 20CTCh. 2 - Prob. 21CTCh. 2 - Prob. 22CTCh. 2 - Prob. 23CT
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Finding Local Maxima and Minima by Differentiation; Author: Professor Dave Explains;https://www.youtube.com/watch?v=pvLj1s7SOtk;License: Standard YouTube License, CC-BY