Chapter 18.3, Problem 18.129P

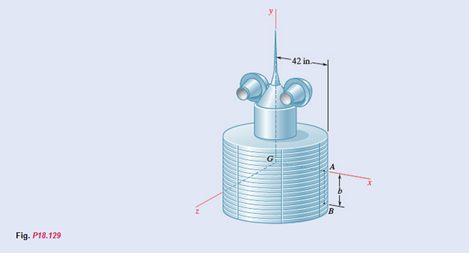
An 800-lb geostationary satellite is spinning with an angular velocity ${\omega }_0=\left(1.5\text{rad/s}\right)\text{j}$ when it is hit at B by a 6-oz meteorite traveling with a velocity $v_0=-\left(1600\text{ft/s}\right)\text{i}+\left(1300\text{ft/s}\right)\text{j}+\left(4000\text{ft/s}\right)\text{k}$ relative to the satellite. Knowing that $b=20$ in. and that the radii of gyration of the satellite are ${\bar{k}}_x={\bar{k}}_z=28.8$ in. and ${\bar{k}}_y=32.4$ in., determine the precession axis and the rates of precession and spin of the satellite after the impact.

  

To determine

The precession angles.

The rate of precession of the satellite after the impact.

The rate of spin axis of the satellite after the impact.

Answer to Problem 18.129P

Thus, the precession angles about the x-axis, y-axis and z-axis are ${125}^0$, ${36.70}^0$ and ${80.7}^0$ respectively.

The rate of precession of the satellite after impact is $0.942\text{rad}/\text{s}$.

The rate of spin axis of the satellite after impact is $0.1561\text{rad}/\text{s}$.

Explanation of Solution

Given information:

The weight of the geostationary satellite is $800\text{lb}$, angular velocity of the satellite is $1.5\left(\text{rad}/\text{s}\right)j$, the weight of the meteorite is $6\text{oz}$, the initial velocity of the meteorite is $\left(-1600\text{ft/s}\right)\text{i}+\left(1300\text{ft/s}\right)j+\left(4000\text{ft/s}\right)k$, the radius of gyration of the satellite along x-and z axes are $28.8\text{in}\text{.}$, the radius of gyration of the satellite along y-axis is $32.4\text{in}\text{.}$, the distance between point B and $G$ is $\left(42\text{in}\text{.}\right)i-\left(20\text{in}\right)j$.

Write the expression of the mass of the meteorite.

$m_M=\frac{W_M}{g}$   ....... (I)

Here, weight of the meteorite is $W_M$ and gravitational acceleration is $g$.

Write the expression of the mass of the satellite.

$m_S=\frac{W_S}{g}$   ....... (II)

Here, weight of the meteorite is $W_S$.

Write the Expression of the moment of inertia along x-axis.

${\overline{I}}_x=m_S{k}_x{}^2$   ....... (III)

Here, the radius of gyration of the satellite along x-axis is $k_x$.

Write the Expression of the moment of inertia along the y-axis.

${\overline{I}}_y=m_S{k}_y{}^2$   ....... (IV)

Here, the radius of gyration of the satellite along y-axis is $k_y$.

Write the Expression of the moment of inertia along z-axis.

${\overline{I}}_z=m_S{k}_z{}^2$   ....... (V)

Here, the radius of gyration of the satellite along z-axis is $k_z$.

Write the expression of the initial momentum of the meteorite.

$M_0=m_M{v}_0$   ....... (VI)

Here, the initial velocity of meteorite is $v_0$.

Write the expression of initial angular momentum of the satellite before the impact.

${\left(H_G\right)}_S={\overline{I}}_x{\left({\omega }_x\right)}_{0}i+{\overline{I}}_y{\left({\omega }_y\right)}_{0}j+{\overline{I}}_z{\left({\omega }_z\right)}_{0}k$   ....... (VII)

Here, the initial angular velocity along x-axis is ${\left({\omega }_x\right)}_0$, the initial angular velocity along y-axis is ${\left({\omega }_y\right)}_0$, the initial angular velocity along z-axis is ${\left({\omega }_z\right)}_0$.

Write the expression of the angular momentum about point B before impact.

${\left(H_G\right)}_B=r_{BG}\times M_0+{\left(H_G\right)}^{\prime }{}_S$   ....... (VIII)

Write the expression of angular momentum of the satellite after impact.

${\left(H_G\right)}^{\prime }{}_S={\overline{I}}_x{\omega }_{x}i+{\overline{I}}_y{\omega }_{y}j+{\overline{I}}_z{\omega }_{z}k$

Here, the angular velocity after impact along x-axis is ${\omega }_x$, the initial angular velocity after impact along y-axis is ${\omega }_y$, the initial angular velocity after the impact along z-axis is ${\omega }_z$.

According to the momentum equilibrium, the angular momentum before and after the impact of meteorite at point B will be same.

${\left(H_G\right)}_B={\left(H_G\right)}^{\prime }{}_S$   ....... (X)

Write the expression of magnitude net angular velocity after impact of meteorite.

$\begin{array}{c}\omega ={\omega }_{x}i+{\omega }_{y}j+{\omega }_{z}k\\ \omega =\sqrt{{\left({\omega }_x\right)}^2+{\left({\omega }_y\right)}^2+{\left({\omega }_y\right)}^2}\end{array}$   ....... (XI)

Write the expression of magnitude net angular momentum after impact of meteorite.

$H_G=\sqrt{{\left(I_x{\omega }_x\right)}^2+{\left(I_y{\omega }_y\right)}^2+{\left(I_y{\omega }_y\right)}^2}$   ....... (XII)

The satellite is symmetrical about y-axis.

Write the expression of moment of inertia along the symmetry axis.

$I={\overline{I}}_y$

Figure-(1) shows the precession axis and the spin axis.

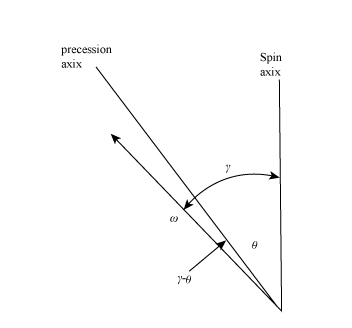
Figure-(1)

Here, angle of precession axis with respect to x, y and z axes is defined in cosine, the angular velocity is $\omega$, the angle of angular velocity with spin axis is $\gamma$.

Write the expression of the angle of precession axis with respect to x-axis.

$\cos {\theta }_x=\frac{{\overline{I}}_x{\omega }_x}{H_G}$   ....... (XIII)

Here, the angle of precession axis with respect to x-axis is ${\theta }_x$.

Write the expression of the angle of precession axis with respect to y-axis.

$\cos {\theta }_y=\frac{{\overline{I}}_y{\omega }_y}{H_G}$   ....... (XIV)

Here, the angle of precession axis with respect to x-axis is ${\theta }_y$.

Write the expression of the angle of precession axis with respect to y-axis.

$\cos {\theta }_z=\frac{{\overline{I}}_z{\omega }_z}{H_G}$   ....... (XV)

Here, the angle of precession axis with respect to x-axis is ${\theta }_z$.

Figure-(2) shows the angle of spin axis with respect to precession axis is constant.

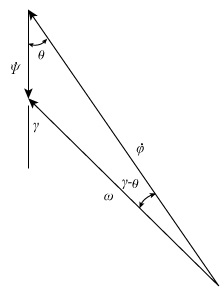
Figure-(2)

Here, the rate of precession is $\dot{\phi }$, and rate of spin is $\dot{\psi }$.

Write the expression of the angle of precession axis with respect to spin axis is constant from figure (2).

$\theta ={\theta }_y$   ....... (XVI)

Write the expression of the angle of angular velocity with respect to spin axis.

$\cos \gamma =\frac{{\omega }_y}{\omega }$   ....... (XVII)

Here, the angle of angular velocity with respect to spin axis is $\gamma$.

Write the expression for relation between $\dot{\phi }$, $\dot{\psi }$ and $\omega$ according to sine rule.

$\frac{\dot{\psi }}{\sin \left(\gamma -\theta \right)}=\frac{\omega }{\sin \theta }=\frac{\dot{\phi }}{\sin \gamma }$   ....... (XVIII)

Calculation:

Substitute $800\text{lb}$ for $W_S$ and $32.2\left(\text{ft}/{\text{s}}^{\text{2}}\right)$ for $g$ in Equation (II).

$\begin{array}{c}{m}_S=\frac{800\text{lb}}{32.2\left(\text{ft}/{\text{s}}^{\text{2}}\right)}\\ =24.844\left(lb\cdot {\text{s}}^{\text{2}}/\text{ft}\right)\end{array}$

Substitute $6\text{oz}$ for $W_M$, and $32.2\left(\text{ft}/{\text{s}}^{\text{2}}\right)$ in Equation (I).

$\begin{array}{c}{m}_M=\frac{6\text{oz}\left(\frac{1\text{lb}}{16\text{oz}}\right)}{32.2\left(\text{ft}/{\text{s}}^{\text{2}}\right)}\\ =\frac{0.375\text{lb}}{32.2\left(\text{ft}/{\text{s}}^{\text{2}}\right)}\\ =0.0116\left({\text{lb×s}}^{\text{2}}/\text{ft}\right)\end{array}$

Substitute $28.8\text{in}\text{.}$ for $k_x$, and $24.844\left(lb\cdot {\text{s}}^{\text{2}}/\text{ft}\right)$ for $m_S$ in Equation (III).

$\begin{array}{c}{\overline{I}}_x=24.844\left(\text{lb}\cdot {\text{s}}^{\text{2}}/\text{ft}\right){\left(28.8\text{in}\text{.}\right)}^2\\ =24.844\left(\text{lb}\cdot {\text{s}}^{\text{2}}/\text{ft}\right){\left(28.8\text{in}\text{.}\left(\frac{1\text{ft}}{12\text{in}\text{.}}\right)\right)}^2\\ =24.844\left(\text{lb}\cdot {\text{s}}^{\text{2}}/\text{ft}\right){\left(2.4\text{ft}\right)}^2\\ =143.101\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)\end{array}$

Substitute $32.4\text{in}\text{.}$ for $k_y$, and $24.844\left(lb\cdot {\text{s}}^{\text{2}}/\text{ft}\right)$ for $m_S$. in Equation (IV).

$\begin{array}{c}{\overline{I}}_y=24.844\left(\text{lb}\cdot {\text{s}}^{\text{2}}/\text{ft}\right){\left(32.4\text{in}\text{.}\right)}^2\\ =24.844\left(\text{lb}\cdot {\text{s}}^{\text{2}}/\text{ft}\right){\left(32.4\text{in}\text{.}\left(\frac{1\text{ft}}{12\text{in}\text{.}}\right)\right)}^2\\ =24.844\left(\text{lb}\cdot {\text{s}}^{\text{2}}/\text{ft}\right){\left(2.7\text{ft}\right)}^2\\ =181.112\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)\end{array}$

Substitute $28.8\text{in}\text{.}$ for $k_z$, and $24.844\left(lb\cdot {\text{s}}^{\text{2}}/\text{ft}\right)$ for $m_S$. in Equation (V).

$\begin{array}{c}{\overline{I}}_z=24.844\left(\text{lb}\cdot {\text{s}}^{\text{2}}/\text{ft}\right){\left(28.8\text{in}\text{.}\right)}^2\\ =24.844\left(\text{lb}\cdot {\text{s}}^{\text{2}}/\text{ft}\right){\left(28.8\text{in}\text{.}\left(\frac{1\text{ft}}{12\text{in}\text{.}}\right)\right)}^2\\ =24.844\left(\text{lb}\cdot {\text{s}}^{\text{2}}/\text{ft}\right){\left(2.4\text{ft}\right)}^2\\ =143.101\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)\end{array}$

Substitute in $\left(-1600\text{ft/s}\right)\text{i}+\left(1300\text{ft/s}\right)j+\left(4000\text{ft/s}\right)k$ for $v_0$, and $0.0116\left({\text{lb×s}}^{\text{2}}/\text{ft}\right)$ for $m_M$ Equation (VI).

$\begin{array}{c}{M}_0=0.0116\left(\text{lb}\cdot {\text{s}}^{\text{2}}/\text{ft}\right)\left[\left(-1600\text{ft/s}\right)\text{i}+\left(1300\text{ft/s}\right)j+\left(4000\text{ft/s}\right)k\right]\\ =\left[\left(-18.56\right)\text{i}+\left(15.08\right)j+\left(46.4\right)k\right]\left(\frac{\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}}{\text{s}\cdot \text{ft}}\right)\\ =\left[\left(-18.56\right)\text{i}+\left(15.08\right)j+\left(46.4\right)k\right]\left(\text{lb}\cdot \text{s}\right)\end{array}$

Substitute $143.101\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)$ for ${\overline{I}}_x$, $181.112\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)$ for ${\overline{I}}_y$, $143.101\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)$ for ${\overline{I}}_z$, $0$ for ${\omega }_x$, $0$ for ${\omega }_y$, $1.5\left(\text{rad}/\text{s}\right)j$ for ${\omega }_z$ in Equation (VII).

$\begin{array}{c}{\left(H_G\right)}_S=\left[\begin{array}{l}\left(143.101\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)\right)\left(0\right)i+\\ \left(181.112\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)\right)\left(1.5\left(\text{rad}/\text{s}\right)\right)j+\\ \left(143.101\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)\right)\left(0\right)k\end{array}\right]\\ =271.668\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)j\end{array}$

Substitute $\left(42\text{in}\text{.}\right)i-\left(20\text{in}\right)j$ for $r_{BG}$, $\left[\left(-18.56\right)\text{i}+\left(15.08\right)j+\left(46.4\right)k\right]\left(\text{lb}\cdot \text{s}\right)$ for $M_0$, and $271.668\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)j$ for ${\left(H_G\right)}_S$ in Equation (VIII).

${\left(H_G\right)}_B=\left[\begin{array}{l}\left(42\text{in}\text{.}\right)i-\\ \left(20\text{in}\right)j\end{array}\right]\times \left[\left[\begin{array}{l}\left(-18.56\right)\text{i}+\\ \left(15.08\right)j+\\ \left(46.4\right)k\end{array}\right]\left(\text{lb}\cdot \text{s}\right)\right]+\left[271.668\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)j\right]$

${\left(H_G\right)}_B=\left[\begin{array}{l}\left(42\text{in}\text{.}\left(\frac{1\text{ft}}{12\text{in}\text{.}}\right)\right)i-\\ \left(20\text{in}\text{.}\left(\frac{1\text{ft}}{12\text{in}\text{.}}\right)\right)j\end{array}\right]\times \left[\left[\begin{array}{l}\left(-18.56\right)\text{i}+\\ \left(15.08\right)j+\\ \left(46.4\right)k\end{array}\right]\left(\text{lb}\cdot \text{s}\right)\right]+\left[271.668\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)j\right]$

${\left(H_G\right)}_B=\left[\begin{array}{l}\left(3.5\text{ft}\right)i-\\ \left(1.67\text{ft}\right)j\end{array}\right]\times \left[\left[\begin{array}{l}\left(-18.56\right)\text{i}+\\ \left(15.08\right)j+\\ \left(46.4\right)k\end{array}\right]\left(\text{lb}\cdot \text{s}\right)\right]+\left[271.668\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)j\right]$

${\left(H_G\right)}_B=\left|\begin{array}{ccc}i& j& k\\ 3.5& -1.67& 0\\ -18.56& 15.08& 46.4\end{array}\right|\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)+\left[271.668\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)j\right]$

$\begin{array}{c}{\left(H_G\right)}_B=\left[\begin{array}{l}\left(-77.64\right)i+\\ \left(-163.044\right)j+\\ \left(21.935\right)k\end{array}\right]\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)+\left[271.668\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)j\right]\\ {\left(H_G\right)}_B=\left[\begin{array}{l}\left(-77.64\right)i+\\ \left(108.624\right)j+\\ \left(21.935\right)k\end{array}\right]\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)\end{array}$

Substitute $\left[\begin{array}{l}\left(-77.64\right)i+\\ \left(108.624\right)j+\\ \left(21.935\right)k\end{array}\right]\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)$ for ${\left(H_G\right)}_B$, and ${\overline{I}}_x{\omega }_{x}i+{\overline{I}}_y{\omega }_{y}j+{\overline{I}}_z{\omega }_{z}k$ for ${\left(H_G\right)}^{\prime }{}_S$ in Equation (X).

$\left[\begin{array}{l}\left(-77.64\right)i+\\ \left(108.624\right)j+\\ \left(21.935\right)k\end{array}\right]\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)={\overline{I}}_x{\omega }_{x}i+{\overline{I}}_y{\omega }_{y}j+{\overline{I}}_z{\omega }_{z}k$   ....... (XIX)

Equate x-components in Equation (XIX) on both side and substitute $143.101\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)$ for ${\overline{I}}_x$.

$\begin{array}{c}\left(-77.64\right)\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)=\left(143.101\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)\right){\omega }_x\\ {\omega }_x=\frac{\left(-77.64\right)\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)}{143.101\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)}\\ {\omega }_x=-0.542\text{rad}/\text{s}\end{array}$

Equate y-components in Equation (XIX) on both side and substitute $181.112\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)$ for ${\overline{I}}_y$.

$\begin{array}{c}\left(108.624\right)j\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)=\left(181.112\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)\right){\omega }_{y}j\\ {\omega }_y=\frac{\left(108.624\right)\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)}{181.112\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)}\\ {\omega }_y=0.599\text{rad}/\text{s}\end{array}$

Equate z-components in Equation (XIX) on both side and substitute $43.101\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)$ for ${\overline{I}}_z$.

$\begin{array}{c}\left(21.935\right)\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)=\left(143.101\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)\right){\omega }_z\\ {\omega }_z=\frac{\left(21.935\right)\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)}{143.101\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)}\\ {\omega }_z=0.153\text{rad}/\text{s}\end{array}$

Substitute $-0.542\text{rad}/\text{s}$ for ${\omega }_x$, $0.599\text{rad}/\text{s}$ for ${\omega }_y$, and $0.153\text{rad}/\text{s}$ for ${\omega }_z$ in Eqaution (XI).

$\begin{array}{c}\omega =\sqrt{{\left(-0.542\text{rad}/\text{s}\right)}^2+{\left(0.599\text{rad}/\text{s}\right)}^2+{\left(0.153\text{rad}/\text{s}\right)}^2}\\ \omega =0.822\text{rad}/\text{s}\end{array}$

Substitute $\left(-77.64\right)\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)$ for $\left(I_x{\omega }_x\right)$, $\left(108.624\right)\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)$ for $\left(I_y{\omega }_y\right)$, and $\left(21.935\right)\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)$ for $\left(I_z{\omega }_z\right)$ in Eqaution (XII).

$\begin{array}{c}{H}_G=\sqrt{{\left(-77.64\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)\right)}^2+{\left(108.624\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)\right)}^2+{\left(21.935\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)\right)}^2}\\ =\sqrt{6027.969+11799.173+481.144}\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)\\ =135.308\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)\end{array}$

Substitute $143.101\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)$ for ${\overline{I}}_x$, $-0.542\text{rad}/\text{s}$ for ${\omega }_x$, $135.308\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)$ for $H_G$ in Equation (XIII).

$\begin{array}{c}\cos {\theta }_x=\frac{143.101\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)\times -0.542\text{rad}/\text{s}}{135.308\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)}\\ \cos {\theta }_x=-0.5732\\ {\theta }_x={124.97}^0\\ \approx {125}^0\end{array}$

Substitute $181.112\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)$ for ${\overline{I}}_y$, $0.599\text{rad}/\text{s}$ for ${\omega }_y$, $135.308\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)$ for $H_G$ in Equation (XIV).

$\begin{array}{c}\cos {\theta }_y=\frac{181.112\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)\times 0.599\text{rad}/\text{s}}{135.308\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)}\\ \cos {\theta }_y=0.80177\\ {\theta }_y={36.70}^0\end{array}$

Substitute $143.101\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)$ for ${\overline{I}}_z$, $0.153\text{rad}/\text{s}$ for ${\omega }_z$, $135.308\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)$ for $H_G$ in Equation (XIV).

$\begin{array}{c}\cos {\theta }_z=\frac{143.101\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)\times 0.153\text{rad}/\text{s}}{135.308\left(\text{lb}\cdot \text{s}\cdot \text{ft}\right)}\\ \cos {\theta }_z=0.1618\\ {\theta }_z={80.687}^0\\ \approx {80.7}^0\end{array}$

Substitute ${36.70}^0$ for ${\theta }_y$ in Equation (XVI).

$\theta ={36.70}^0$

Substitute $0.599\text{rad}/\text{s}$ for ${\omega }_y$, and $0.822\text{rad}/\text{s}$ for $\omega$ in Equation (XVII).

$\begin{array}{l}\cos \gamma =\frac{0.599\text{rad}/\text{s}}{0.822\text{rad}/\text{s}}\\ \cos \gamma =0.7287\\ \gamma ={43.22}^0\end{array}$

Compare first and second term of Equation (XVIII).

$\frac{\dot{\psi }}{\sin \left(\gamma -\theta \right)}=\frac{\omega }{\sin \theta }$   ....... (XX)

Substitute ${43.22}^0$ for $\gamma$, ${36.70}^0$ for $\theta$, $0.822\text{rad}/\text{s}$ for $\omega$ in Equation (XX).

$\begin{array}{c}\frac{\dot{\psi }}{\sin \left({43.22}^0-{36.70}^0\right)}=\frac{0.822\text{rad}/\text{s}}{\sin {36.70}^0}\\ \dot{\psi }=\frac{\left(0.822\text{rad}/\text{s}\right)\left(0.1135\right)}{0.5976}\\ \dot{\psi }=0.1561\text{rad}/\text{s}\end{array}$

Compare second and third term of Equation (XVIII).

$\frac{\omega }{\sin \theta }=\frac{\dot{\phi }}{\sin \gamma }$   ....... (XXI)

Substitute ${43.22}^0$ for $\gamma$, ${36.70}^0$ for $\theta$, $0.822\text{rad}/\text{s}$ for $\omega$ in Equation (XXI).

$\begin{array}{c}\frac{0.822\text{rad}/\text{s}}{\sin {36.70}^0}=\frac{\dot{\phi }}{\sin {43.22}^0}\\ \dot{\phi }=\frac{\left(0.822\text{rad}/\text{s}\right)\left(0.6848\right)}{0.5976}\\ \dot{\phi }=0.942\text{rad}/\text{s}\end{array}$

Conclusion:

Thus, the precession angle about the x-axis, y-axis and z-axis are ${125}^0$, ${36.70}^0$ and ${80.7}^0$.

The rate of precession of the satellite after impact is $0.942\text{rad}/\text{s}$.

The rate of spin axis of the satellite after impact is $0.1561\text{rad}/\text{s}$.