Chapter 18.1, Problem 18.54P

To determine

The kinetic energy of the space probe after its collision with the meteorite.

Answer to Problem 18.54P

The kinetic energy of the space probe after its collision with the meteorite is $2.436\times {10}^6\left(\text{ft}\cdot \text{lb}\right)$.

Explanation of Solution

Given information:

The weight of the space probe is $3000\text{lb}$, the weight of the meteorite is $5\text{oz}$, the radius of gyration of space probe along the x-axis is $1.375\text{ft}$, the radius of gyration of space probe along the y-axis is $1.425\text{ft}$, the radius of gyration along the z-axis is $1.250\text{ft}$, and final angular velocity of the space probe is $\left(0.05\text{rad}/\text{s}\right)i-\left(0.12\text{rad}/\text{s}\right)j+\left({\omega }_z\text{rad}/\text{s}\right)k$. The angular momentum of the space probe is reduced by $25\%$. The resulting change in x component of mass centre of the space probe is $-0.675\left(\text{in}\text{.}/s\right)$.

Write the expression of the mass of the meteorite.

$m_M=\frac{W_M}{g}$ ...... (I)

Here, weight of the meteorite is $W_M$ and gravitational acceleration is $g$.

Write the expression of the mass of the space probe.

$m_P=\frac{W_P}{g}$ ...... (II)

Here, weight of the meteorite is $W_P$.

Write the expression of angular momentum of the meteorite about $G$.

${\left(H_G\right)}_M=r_A\times m_M{v}_0$ ...... (III)

Here, the distance of point A is $r_A$, the mass of the meteorite is $m_M$, and the initial velocity of the meteorite is $v_0$.

Write the Expression of the moment of inertia along x-axis.

${\overline{I}}_x=m{k}_x{}^2$ ...... (IV)

Here, the radius of gyration of the space probe along x-axis is $k_x$.

Write the Expression of the moment of inertia along the y-axis.

${\overline{I}}_y=m{k}_y{}^2$ ...... (V)

Here, the radius of gyration of the space probe along y-axis is $k_y$.

Write the Expression of the moment of inertia along z-axis.

${\overline{I}}_z=m{k}_z{}^2$ ...... (VI)

Here, the radius of gyration of the space probe along z-axis is $k_z$.

Write the expression of angular momentum of space probe.

${\left(H_G\right)}_P={\overline{I}}_x{\omega }_{x}i+{\overline{I}}_y{\omega }_{y}j+{\overline{I}}_z{\omega }_{z}k$ ...... (VII)

Here, moment of inertia along x-axis is $I_x$, moment of inertia along y-axis is $I_y$, and moment of inertia along z-axis is $I_z$.

Substitute $m{k}_x{}^2$ for ${\overline{I}}_x$, $m{k}_y{}^2$ for ${\overline{I}}_y$ and $m{k}_z{}^2$ for ${\overline{I}}_z$ in Equation (VII).

$\begin{array}{c}{\left(H_G\right)}_P=m{k}_x{}^2{\omega }_{x}i+m{k}_y{}^2{\omega }_{y}j+m{k}_z{}^2{\omega }_{z}k\\ {\left(H_G\right)}_P=m\left(k_x{}^2{\omega }_{x}i+k_y{}^2{\omega }_{y}j+k_z{}^2{\omega }_{z}k\right)\end{array}$ ...... (VIII)

Here, angular velocity along x-axis is ${\omega }_x$, angular velocity along y-axis is ${\omega }_y$, angular velocity along x-axis is ${\omega }_z$, the radius of gyration of space probe along x-axis is $k_x$, the radius of gyration of space probe along y-axis is $k_y$, radius of gyration along z-axis is $k_z$.

Write the expression of kinetic energy of the space probe.

$T=\frac{1}{2}\left(I_x{\omega }_x{}^2+I_y{\omega }_y{}^2+I_z{\omega }_z{}^2\right)$ ...... (IX)

Substitute $m{k}_x{}^2$ for ${\overline{I}}_x$, $m{k}_y{}^2$ for ${\overline{I}}_y$ and $m{k}_z{}^2$ for ${\overline{I}}_z$ in Equation (IX).

$\begin{array}{c}T=\frac{1}{2}\left(m{k}_x{}^2{\omega }_x{}^2+m{k}_y{}^2{\omega }_y{}^2+m{k}_z{}^2{\omega }_z{}^2\right)\\ T=\frac{1}{2}m\left(k_x{}^2{\omega }_x{}^2+k_y{}^2{\omega }_y{}^2+k_z{}^2{\omega }_z{}^2\right)\end{array}$ ...... (X)

Calculation:

Substitute $5\text{oz}$ for $W_P$, and $32.2\text{ft}/{\text{s}}^{\text{2}}$ for $g$ in Equation (I) for the meteorite.

$\begin{array}{c}{m}_M=\frac{\left(5\text{oz}\right)}{\left(32.2\text{ft}/{\text{s}}^{\text{2}}\right)}\\ m_M=\frac{\left(\frac{5}{16}\text{lb}\right)}{\left(32.2\text{ft}/{\text{s}}^{\text{2}}\right)}\end{array}$

Substitute $3000\text{lb}$ for $W_P$, and $32.2\text{ft}/{\text{s}}^{\text{2}}$ for $g$ in Equation (II) for the space probe.

$\begin{array}{c}{m}_P=\frac{\left(3000\text{lb}\right)}{\left(32.2\text{ft}/{\text{s}}^{\text{2}}\right)}\\ m_P=93.167\left(\frac{\text{lb}\cdot {\text{s}}^{\text{2}}}{\text{ft}}\right)\end{array}$

Write the expression that shows the relation between linear momentum of meteorite and the space probe.

$25\%\left(m_M\right){\left(v_0\right)}_x=\left(m_P\right){\left(\Delta v\right)}_x$ ...... (XI)

Here, the initial velocity along x-axis is ${\left(v_0\right)}_x$, and change in velocity of probe in x-axis is ${\left(\Delta v\right)}_x$.

Substitute $\frac{\left(\frac{5}{16}\text{lb}\right)}{\left(32.2\text{ft}/{\text{s}}^{\text{2}}\right)}$ for $m_M$, and $93.167\left(\frac{\text{lb}\cdot {\text{s}}^{\text{2}}}{\text{ft}}\right)$ for $m_P$ in Equation (XI).

$\begin{array}{c}25\%\left(\frac{\left(\frac{5}{16}\text{lb}\right)}{\left(32.2\text{ft}/{\text{s}}^{\text{2}}\right)}\right){\left(v_0\right)}_x=\left(93.167\left(\frac{\text{lb}\cdot {\text{s}}^{\text{2}}}{\text{ft}}\right)\right)\left(-0.675\left(\text{in}\text{.}/s\right)\right)\\ 0.25\left(\frac{\left(9.705\times {10}^{\left(-3\right)}\text{lb}\right)}{\left(\text{ft}/{\text{s}}^{\text{2}}\right)}\right){\left(v_0\right)}_x=\left(93.167\left(\frac{\text{lb}\cdot {\text{s}}^{\text{2}}}{\text{ft}}\right)\right)\left(-0.675\left(\text{in}\text{.}/s\right)\right)\\ 2.426\times {10}^{\left(-3\right)}\frac{\left(\text{lb}\right)}{\left(\text{ft}/{\text{s}}^{\text{2}}\right)}{\left(v_0\right)}_x=\left(-62.887\left(\frac{\text{lb}\cdot {\text{s}}^{\text{2}}}{\text{ft}}\right)\right)\left(\text{in}\text{.}/s\right)\\ {\left(v_0\right)}_x=-25.92\times {10}^3\left(\text{in}\text{.}/s\right)\end{array}$

$\begin{array}{c}{\left(v_0\right)}_x=-25.92\times {10}^3\left(\frac{1}{12}\text{ft}\right)/\text{s}\\ =\frac{-25.92\times {10}^3}{12}\left(\text{ft}/\text{s}\right)\\ =-2160\left(\text{ft}/\text{s}\right)\end{array}$

Substitute ${\left(v_0\right)}_{x}i-{\left(v_0\right)}_{y}j+{\left(v_0\right)}_{z}k$ for $v_0$ in Equation (III).

$\begin{array}{l}{\left(H_G\right)}_M=r_A\times m_M\left({\left(v_0\right)}_{x}i-{\left(v_0\right)}_{y}j+{\left(v_0\right)}_{z}k\right)\\ \end{array}$ ...... (XII)

Substitute $\left[(9\text{ft})i+\left(0.75\text{ft}\right)k\right]$ for $r_A$, $\frac{\left(\frac{5}{16}\text{lb}\right)}{\left(32.2\text{ft}/{\text{s}}^{\text{2}}\right)}$ for $m_M$, and $-2160\left(\text{ft}/s\right)$ for ${\left(v_0\right)}_x$ in Equation (XII).

$\begin{array}{c}{\left(H_G\right)}_M=\left[(9\text{ft})i+\left(0.75\text{ft}\right)k\right]\times \frac{\left(\frac{5}{16}\text{lb}\right)}{\left(32.2\text{ft}/{\text{s}}^{\text{2}}\right)}\left(-2160\left(\text{ft}/s\right)i-{\left(v_0\right)}_{y}j+{\left(v_0\right)}_{z}k\right)\\ =9.704\times {10}^{\left(-3\right)}\frac{\left(\text{lb}\right)}{\left(\text{ft}/{\text{s}}^{\text{2}}\right)}\left|\begin{array}{ccc}i& j& k\\ 9& 0& 0.75\\ -2160& {\left(v_0\right)}_y& {\left(v_0\right)}_z\end{array}\right|\\ =9.704\times {10}^{\left(-3\right)}\frac{\left(\text{lb}\right)}{\left(\text{ft}/{\text{s}}^{\text{2}}\right)}\left(-0.75\text{ft}{\left(v_0\right)}_{y}i-\left(9\text{ft}{\left(v_0\right)}_z+1620\left({\text{ft}}^2/\text{s}\right)\right)j+9\text{ft}{\left(v_0\right)}_{z}k\right)\end{array}$

Substitute $1.375\text{ft}$ for $k_x$, $1.425\text{ft}$ for $k_y$, $1.250\text{ft}$ for $k_z$, $\left(0.05\text{rad}/\text{s}\right)$ for ${\omega }_x$, $-\left(0.12\text{rad}/\text{s}\right)$ for ${\omega }_y$, and $93.167\left(\frac{\text{lb}\cdot {\text{s}}^{\text{2}}}{\text{ft}}\right)$ for $m$ in Equation (III).

$\begin{array}{c}{\left(H_G\right)}_P=93.167\left(\frac{\text{lb}\cdot {\text{s}}^{\text{2}}}{\text{ft}}\right)\left(\begin{array}{l}{\left(1.375\text{ft}\right)}^2\left(0.05\text{rad}/\text{s}\right)i-{\left(1.425\text{ft}\right)}^2\left(0.12\text{rad}/\text{s}\right)j+\\ {\left(1.250\text{ft}\right)}^2{\omega }_{z}k\end{array}\right)\\ {\left(H_G\right)}_P=\left(\begin{array}{l}\left(8.8071\text{rad}/\text{s}\right)i-\left(22.702\text{rad}/\text{s}\right)j+\\ \left(145.57\right){\omega }_{z}k\end{array}\right)\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)\end{array}$

The angular momentum of the space probe is $25\%$ of the angular momentum of the meteorite.

Write the expression of the relation between ${\left(H_G\right)}_P$ and ${\left(H_G\right)}_M$.

$\begin{array}{l}{\left(H_G\right)}_P=25\%{\left(H_G\right)}_M\\ {\left(H_G\right)}_P=\frac{{\left(H_G\right)}_M}{4}\end{array}$ ...... (XIII)

Substitute $\left(9.704\times {10}^{\left(-3\right)}\frac{\left(\text{lb}\right)}{\left(\text{ft}/{\text{s}}^{\text{2}}\right)}\left(-0.75\text{ft}{\left(v_0\right)}_{y}i-\left(9\text{ft}{\left(v_0\right)}_z+1620\left({\text{ft}}^2/\text{s}\right)\right)j+9\text{ft}{\left(v_0\right)}_{z}k\right)\right)$ for ${\left(H_G\right)}_M$, and $\left(\begin{array}{l}\left(8.8071\text{rad}/\text{s}\right)i-\left(22.702\text{rad}/\text{s}\right)j+\\ \left(145.57\right){\omega }_{z}k\end{array}\right)\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)$ for ${\left(H_G\right)}_P$ in Equation (XIII).

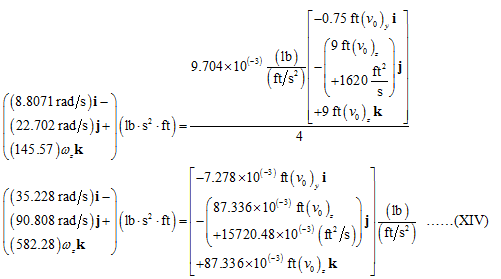
Compare x-component of Equation (IX) on both side.

$\begin{array}{c}\left(35.228\text{rad}/\text{s}\right)\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)=\left(7.278\times {10}^{\left(-3\right)}\text{ft}\right){\left(v_0\right)}_y\frac{\left(\text{lb}\right)}{\left(\text{ft}/{\text{s}}^{\text{2}}\right)}\\ {\left(v_0\right)}_y=-4840.3\left(\text{ft}/\text{s}\right)\end{array}$

Compare y-component of Equation (XIV) on both side.

$\begin{array}{c}-\left(90.808\right)\frac{\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)}{\text{s}}=\left[-\left(\begin{array}{l}87.336\times {10}^{\left(-3\right)}\text{ft}{\left(v_0\right)}_z\\ +15720.48\times {10}^{\left(-3\right)}\left({\text{ft}}^2/\text{s}\right)\end{array}\right)\right]\frac{\left(\text{lb}\right)}{\left(\text{ft}/{\text{s}}^{\text{2}}\right)}\\ -\left(90.808\right)\frac{\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)}{\text{s}}=\left[\left(\begin{array}{l}-87.336\times {10}^{\left(-3\right)}\left(\text{lb}\cdot {\text{s}}^{\text{2}}\right){\left(v_0\right)}_z\\ -15720.48\times {10}^{\left(-3\right)}\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}/s\right)\end{array}\right)\right]\\ -15810.808\frac{\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)}{\text{s}}=-87.336\times {10}^{\left(-3\right)}\left(\text{lb}\cdot {\text{s}}^{\text{2}}\right){\left(v_0\right)}_z\\ {\left(v_0\right)}_z=1219.74\left(\text{ft}/s\right)\end{array}$

Compare z-component of Equation (XIV) on both side.

$\left(\left(582.28\right){\omega }_z\right)\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)=\left[\left(87.336\times {10}^{\left(-3\right)}\text{ft}\right){\left(v_0\right)}_z\right]\frac{\left(\text{lb}\right)}{\left(\text{ft}/{\text{s}}^{\text{2}}\right)}$ ...... (XV)

Substitute $181.039\left(\text{ft}/s\right)$ for ${\left(v_0\right)}_z$ in Equation (XV).

$\begin{array}{c}\left(\left(582.28\right){\omega }_z\right)\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)=\left[\left(87.336\text{ft}\right)\left(1219.74\left(\text{ft}/s\right)\right)\right]\frac{\left(\text{lb}\right)}{\left(\text{ft}/{\text{s}}^{\text{2}}\right)}\\ {\omega }_z=\left[\frac{\left(87.336\right)\left(1219.74\right)}{\left(582.28\right)}\right]\frac{\text{ft}\left(\text{ft}/s\right)\left(\text{lb}\cdot {\text{s}}^{\text{2}}\right)}{\text{ft}\left(\text{lb}\cdot {\text{s}}^{\text{2}}\cdot \text{ft}\right)}\\ {\omega }_z=182.948\left(\text{rad}/\text{s}\right)\end{array}$

Substitute $1.375\text{ft}$ for $k_x$, $1.425\text{ft}$ for $k_y$, $1.250\text{ft}$ for $k_z$, $\left(0.05\text{rad}/\text{s}\right)$ for ${\omega }_x$, $\left(-0.12\text{rad}/\text{s}\right)$ for ${\omega }_y$, $182.948\left(\text{rad}/\text{s}\right)$ for ${\omega }_z$, and $93.167\left(\frac{\text{lb}\cdot {\text{s}}^{\text{2}}}{\text{ft}}\right)$ for $m$ in Equation (X).

$\begin{array}{c}T=\frac{1}{2}\left(93.167\left(\frac{\text{lb}\cdot {\text{s}}^{\text{2}}}{\text{ft}}\right)\right)\left[\begin{array}{l}{\left(1.375\text{ft}\right)}^2{\left(0.05\text{rad}/\text{s}\right)}^2\\ +{\left(1.425\text{ft}\right)}^2{\left(-\left(0.12\text{rad}/\text{s}\right)\right)}^2\\ +{\left(1.250\text{ft}\right)}^2{\left(182.948\left(\text{rad}/\text{s}\right)\right)}^2\end{array}\right]\\ =46.583\left(\frac{\text{lb}\cdot {\text{s}}^{\text{2}}}{\text{ft}}\right)\left[\left(4.72\times {10}^{\left(-3\right)}\right)+\left(0.02924\right)+\left(52296.82\right)\right]{\left(\text{ft}/\text{s}\right)}^2\\ =2.436\times {10}^6\left(\text{ft}\cdot \text{lb}\right)\end{array}$

Conclusion:

Thus, the kinetic energy is $2.436\times {10}^6\left(\text{ft}\cdot \text{lb}\right)$.