
Concept explainers
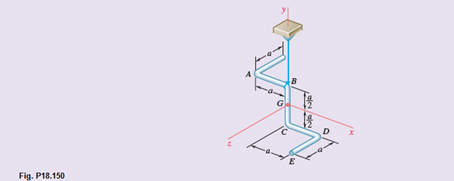
A uniform rod of mass m and length 5a is bent into the shape shown and is suspended from a wire attached at point B. Knowing that the rod is hit at point A in the negative y direction and denoting the corresponding impulse by
The velocity of the mass centre
Answer to Problem 18.150RP
The velocity of the mass centre
Explanation of Solution
Given information:
The mass of the rod is
The below figure represent the schematic diagram of the rod section.
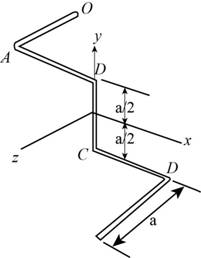
Figure-(1)
Write the expression of length of the section OA.
Here, the total length of the rod is
Write the expression of length of the section AB.
Write the expression of length of the section BC.
Write the expression of length of the section CD.
Write the expression of length of the section DE.
Write the expression of mass of the section OA.
Here, the total mass of the rod is
Write the expression of mass of the section AB.
Write the expression of mass of the section BC.
Write the expression of mass of the section CD.
Write the expression of mass of the section DE.
Write the expression of moment of inertia of section OA in
Write the expression of moment of inertia of section OA in
Write the expression of moment of inertia of section OA in
Write the expression of moment of inertia of section OA in
Write the expression of moment of inertia of section AB in
Write the expression of moment of inertia of section AB in
Write the expression of moment of inertia of section AB in
Write the expression of moment of inertia of section AB in
Write the expression of moment of inertia of section BC in
Write the expression of moment of inertia of section BC in
Write the expression of moment of inertia of section BC in
Write the expression of moment of inertia of section BC in
Write the expression of moment of inertia of section CD in
Write the expression of moment of inertia of section CD in
Write the expression of moment of inertia of section CD in
Write the expression of moment of inertia of section CD in
Write the expression of moment of inertia of section DE in
Write the expression of moment of inertia of section DE in
Write the expression of moment of inertia of section DE in
Write the expression of moment of inertia of section DE in
Write the expression of total moment of inertia in
Write the expression of total moment of inertia in
Write the expression of total moment of inertia in
Write the expression of total moment of inertia in
Write the expression of total moment of inertia in
Write the expression of total moment of inertia in
Write the expression of angular momentum about
Write the expression of angular momentum about
Write the expression of angular momentum about
Write the expression of velocity of mass centre
Here, the force is
Calculation:
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Conclusion:
The velocity of the mass centre
(b)
The angular velocity of the rod.
Answer to Problem 18.150RP
The angular velocity of the rod is
Explanation of Solution
Given information:
Write the expression of angular momentum in
Write the expression of angular velocity of the rod.
Here, the angular velocity in
Calculation:
Substitute
Substitute
Substitute
Substitute
Solve Equation (XXXIII), (XXXIX) and (XXXX).
Substitute
Conclusion:
The angular velocity of the rod is
Want to see more full solutions like this?
Chapter 18 Solutions
Vector Mechanics For Engineers
- A 4 ft 300 Ib 1000 Ib.ft 350 Ib C 2 ft 3. 45° 250 Ib B. 3ft B 25ft 200 Ib 150 Ib Replace the force system acting on the frame shown in the figure by a resultant force (magnitude and direction), and specify where its line of action intersects member (AB), measured from point (A).arrow_forwardCan you research the standard percentage of Steam Quality in:(1.) Boiler - leaving boilerBoiler -> Out(2.) Condenser - coming in condenser In -> CondenserProvide reference Also define: steam quality, its purpose and importancearrow_forwardNumbers 1 and 2 and 5 are are optional problems. However, I only need the values (with units) of 3, 4 and 6. Thank you :)arrow_forward
- Three cables are pulling on a ring located at the origin, as shown in the diagram below. FA is 200 N in magnitude with a transverse angle of 30° and an azimuth angle of 140°. FB is 240 N in magnitude with coordinate direction angles α = 135° and β = 45°. Determine the magnitude and direction of FC so that the resultant of all 3 force vectors lies on the z-axis and has a magnitude of 300 N. Specify the direction of FC using its coordinate direction angles.arrow_forwardturbomachieneryarrow_forwardauto controlsarrow_forward
- auto controlsarrow_forward1 Pleasearrow_forwardA spring cylinder system measures the pressure. Determine which spring can measure pressure between 0-1 MPa with a large excursion. The plate has a diameter of 20 mm. Also determine the displacement of each 0.1 MPa step.Spring power F=c x fF=Springpower(N)c=Spring constant (N/mm)f=Suspension (mm) How do I come up with right answer?arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





