
Concept explainers
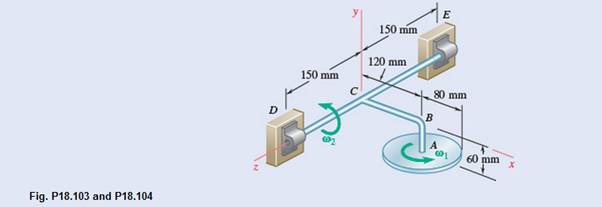
A 2.5-kg homogeneous disk of radius 80 mm rotates at the constant rate
(a)
The couple applied to shaft to produce acceleration.
Answer to Problem 18.104P
The couple applied to shaft to produce acceleration is
Explanation of Solution
Given information:
Mass of homogeneous disk is
The figure is represented below.
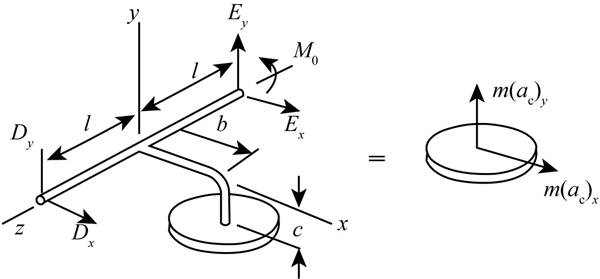
Figure (1)
Write the expression for the angular velocity of disk in x direction.
Write the expression for the total angular velocity of the disk
Here
Substitute,
Write the expression for the angular momentum about point
Here, mass moment of inertia about the x-axis is
Substitute
Write the expression for angular velocity in vector form of shaft
Write the expression for rate of angular velocity of the reference frame
Here,
Write the expression for rate of total angular velocity.
Substitute
Write the expression for Matrix multiplication of the vector product for Equation (10).
Write the expression for the mass moment of inertia about the y-direction.
Here mass of the disk is
Write the expression for the mass moment of inertia about the z- direction.
Substitute
Write the expression for the velocity of mass centre of the disk.
Here, velocity of mass centre is
Write the expression for
Here, horizontal distance is
Substitute
Write the expression for the matrix multiplication of the vector product for Equation (17).
Write the expression for the acceleration of the mass centre of the disk.
Substitute
Write the expression for the matrix multiplication of the vector product for Equation (20).
Write the expression for the the sum of the forces acting on the system.
Here, force at
Write the expression for the force in terms of mass and acceleration.
Substitute
Substitute
Compare the coefficients of the unit vector of
Compare the coefficients of the unit vector of
Write the expression for the rate of angular momentum about
Here, distance of
Write the expression for
Here distance from point
Substitute
Write the expression for the matrix multiplication for vector product for equation (30).
Write the expression for the moment about
Here, moment couple when system is at rest is
Write the expression for the matrix multiplication for the vector product for equation (32).
The sum of the moment at
Substitute
Compare the coefficients of the unit vector of
Calculation:
Substitute values of
Thus value of couple
Conclusion:
The couple applied to shaft to produce acceleration is
(b)
The dynamic reaction at
The dynamic reaction at
Answer to Problem 18.104P
The dynamic reactions at
The dynamic reactions at
Explanation of Solution
Given information:
Compare the coefficients of the unit vector of
Compare the coefficients of the unit vector of
Substitute
Substitute
Write the expression for the angular velocity in terms of time in y-direction.
Write the expression for the angular velocity in terms of time in y-direction
Calculation:
Substitute values of
Substitute values of
Hence, dynamic reaction at
Substitute values of
Substitute values of
Hence, dynamic reaction at
Conclusion:
The dynamic reactions at
The dynamic reactions at
Want to see more full solutions like this?
Chapter 18 Solutions
Vector Mechanics For Engineers
- A garden hose attached with a nozzle is used to fill a 20-gal bucket. The inner diameter of the hose is 1 in and it reduces to 0.53 in at the nozzle exit. The average velocity in the hose is 8 ft/s and the density of water is 62.4 lbm/ft3. NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. Determine the volume and mass flow rates of water through the hose. The volume flow rate of water through the hose is ft3/s. The mass flow rate of water through the hose is lbm/s. The change in time? What is the exit velocity?arrow_forwardA 23-ft3 rigid tank initially contains saturated refrigerant-134a vapor at 160 psia. As a result of heat transfer from the refrigerant, the pressure drops to 50 psia. NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. Determine the final temperature. Use data from refrigerant tables. The final temperature is ºF.arrow_forwardA 23-ft3 rigid tank initially contains saturated refrigerant-134a vapor at 160 psia. As a result of heat transfer from the refrigerant, the pressure drops to 50 psia. NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. Determine the heat transfer. The heat transfer is Btu.arrow_forward
- The shaft shown in the figure below is subjected to axial loads as illustrated. The diameters of segments AB, BC, and CD are 20mm, 25mm, and 15mm, respectively. If the modulus of elasticity of the material is 610 MPa. Determine the change of A to D lengtharrow_forwardDetermine the final pressure and temperature. The final pressure is kPa. The final temperature is ºC.arrow_forwardAir enters the 1-m2 inlet of an aircraft engine at 100 kPa and 20°C with a velocity of 184 m/s. Determine the volume flow rate, in m3/s, at the engine’s inlet and the mass flow rate, in kg/s, at the engine’s exit. The gas constant of air is R = 0.287 kPa·m3/kg·K. The volume flow rate at the engine’s inlet m3/s. The mass flow rate at the engine’s exit is kg/s.arrow_forward
- The ventilating fan of the bathroom of a building has a volume flow rate of 33 L/s and runs continuously. If the density of air inside is 1.20 kg/m3, determine the mass of air vented out in one day. The mass of air is kg.arrow_forwardA steady-flow compressor is used to compress helium from 15 psia and 70°F at the inlet to 200 psia and 600°F at the outlet. The outlet area and velocity are 0.01 ft2 and 100 ft/s, respectively, and the inlet velocity is 53 ft/s. Determine the mass flow rate and the inlet area. The gas constant of helium is R = 2.6809 psia·ft3/lbm·R. The mass flow rate is lbm/s. The inlet area is ft2.arrow_forward1. The maximum and minimum stresses as well as the shear stress seen subjected the piece in plane A-A. Assume it is a cylinder with a diameter of 12.7mm 2. Draw the Mohr circle for the stress state using software. 3. Selection of the material for the prosthesis, which must be analyzed from the point of safety and cost view.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





