
(a)
To find: The scatter graph of given data.
The graph is given
Given information:
| Time(min) | Temperature | Time (L2) | Temperature |
| 1 | 184.3 | 11 | 140 |
| 2 | 178.5 | 12 | 136.1 |
| 3 | 173.5 | 13 | 133.5 |
| 4 | 168.6 | 14 | 130.5 |
| 5 | 164.0 | 15 | 127.9 |
| 6 | 159.2 | 16 | 125 |
| 7 | 155.1 | 17 | 122.8 |
| 8 | 151.8 | 18 | 119.9 |
| 9 | 147 | 19 | 117.2 |
| 10 | 143.7 | 20 | 115.2 |
Graph of time from L1 and temperature from L2 is given below.
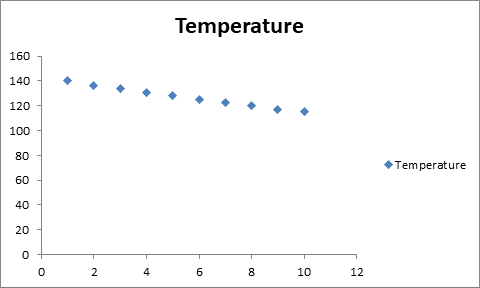
(b)
To find: Store L2-72 and find L3.
The table is given
Given information:
| L3 Time | temperature |
| 21 | 68 |
| 22 | 64.1 |
| 23 | 61.5 |
| 24 | 68.5 |
| 25 | 55.9 |
| 26 | 53 |
| 27 | 50.8 |
| 28 | 47.9 |
| 29 | 45.2 |
| 30 | 43.2 |
(c)
To find: Find the exponential regression for L3.
The exponential regression for L3 is
Given information:
| L3 Time | temperature |
| 21 | 68 |
| 22 | 64.1 |
| 23 | 61.5 |
| 24 | 68.5 |
| 25 | 55.9 |
| 26 | 53 |
| 27 | 50.8 |
| 28 | 47.9 |
| 29 | 45.2 |
| 30 | 43.2 |
The curve to be fitted is
which linear in Y,x
So the corresponding normal equations are
The values are calculated using the following table
| x | y | Y=log10(y) | x2 | x·Y |
| 1 | 68 | 1.8325 | 1 | 1.8325 |
| 2 | 64.1 | 1.8069 | 4 | 3.6137 |
| 3 | 61.5 | 1.7889 | 9 | 5.3666 |
| 4 | 68.5 | 1.8357 | 16 | 7.3428 |
| 5 | 55.9 | 1.7474 | 25 | 8.7371 |
| 6 | 53 | 1.7243 | 36 | 10.3457 |
| 7 | 50.8 | 1.7059 | 49 | 11.941 |
| 8 | 47.9 | 1.6803 | 64 | 13.4427 |
| 9 | 45.2 | 1.6551 | 81 | 14.8962 |
| 10 | 43.2 | 1.6355 | 100 | 16.3548 |
| --- | --- | --- | --- | --- |
| ∑x=55 | ∑y=558.1 | ∑Y=17.4124 | ∑x2=385 | ∑x· Y=93.8731 |
Substituting these values in the normal equations
10A+55B=17.4124
55A+385B=93.8731
Use elimination method we obtain A=1.8676,B=-0.023
∴a=antilog10(A)=antilog10(1.8676)=73.7191 and b=antilog10(B)=antilog10(-0.023)=0.9485
Now substituting this values in the equation is
Chapter 1 Solutions
PRECALCULUS:GRAPH...-NASTA ED.(FLORIDA)
- Which sign makes the statement true? 9.4 × 102 9.4 × 101arrow_forwardDO these math problems without ai, show the solutions as well. and how you solved it. and could you do it with in the time spandarrow_forwardThe Cartesian coordinates of a point are given. (a) (-8, 8) (i) Find polar coordinates (r, 0) of the point, where r > 0 and 0 ≤ 0 0 and 0 ≤ 0 < 2π. (1, 0) = (r. = ([ (ii) Find polar coordinates (r, 8) of the point, where r < 0 and 0 ≤ 0 < 2π. (5, 6) = =([arrow_forward
- The Cartesian coordinates of a point are given. (a) (4,-4) (i) Find polar coordinates (r, e) of the point, where r > 0 and 0 0 and 0 < 0 < 2π. (r, 6) = X 7 (ii) Find polar coordinates (r, 8) of the point, where r < 0 and 0 0 < 2π. (r, 0) = Xarrow_forwardr>0 (r, 0) = T 0 and one with r 0 2 (c) (9,-17) 3 (r, 8) (r, 8) r> 0 r<0 (r, 0) = (r, 8) = X X X x x Warrow_forward74. Geometry of implicit differentiation Suppose x and y are related 0. Interpret the solution of this equa- by the equation F(x, y) = tion as the set of points (x, y) that lie on the intersection of the F(x, y) with the xy-plane (z = 0). surface Z = a. Make a sketch of a surface and its intersection with the xy-plane. Give a geometric interpretation of the result that dy dx = Fx F χ y b. Explain geometrically what happens at points where F = 0. yarrow_forward
- Example 3.2. Solve the following boundary value problem by ADM (Adomian decomposition) method with the boundary conditions მი მი z- = 2x²+3 дг Əz w(x, 0) = x² - 3x, θω (x, 0) = i(2x+3). ayarrow_forward6. A particle moves according to a law of motion s(t) = t3-12t2 + 36t, where t is measured in seconds and s is in feet. (a) What is the velocity at time t? (b) What is the velocity after 3 s? (c) When is the particle at rest? (d) When is the particle moving in the positive direction? (e) What is the acceleration at time t? (f) What is the acceleration after 3 s?arrow_forwardConstruct a table and find the indicated limit. √√x+2 If h(x) = then find lim h(x). X-8 X-8 Complete the table below. X 7.9 h(x) 7.99 7.999 8.001 8.01 8.1 (Type integers or decimals rounded to four decimal places as needed.)arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





