Chapter 1.3, Problem 69E

Solution

a.

To determine which among the twelve basic functions does not have the property $f\left(0\right)=0$ .

The basic functions that do not process the property that $f\left(0\right)=0$:

• The reciprocal function,
• The exponential function,
• The natural logarithm function,
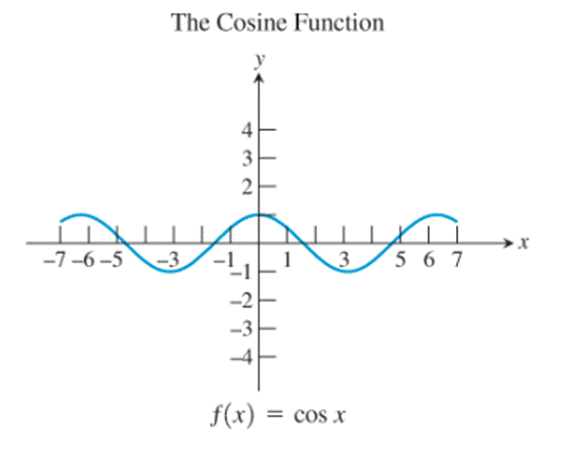
• The cosine function
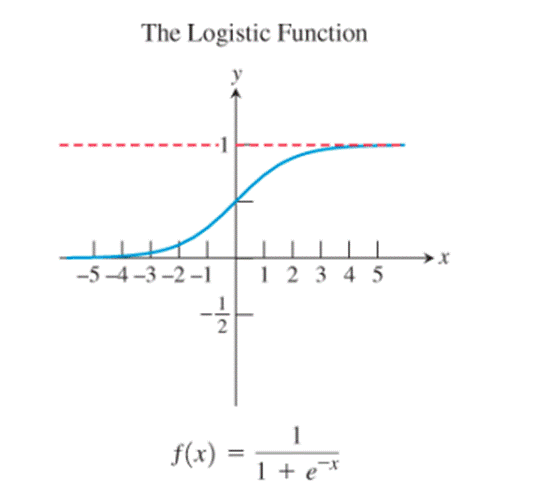
• The logistic function

Concept Used:

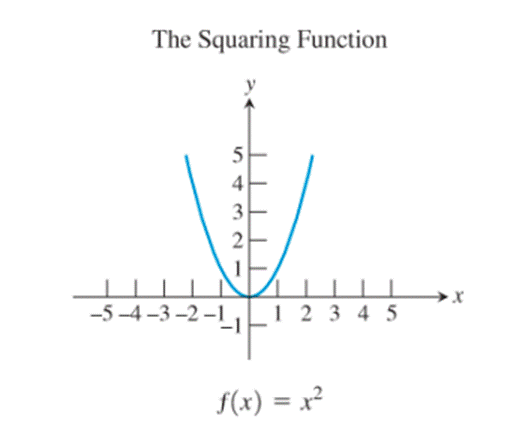
The twelve basic functions:

1)

  

2)

  

3)

  

4)

  

5)

  

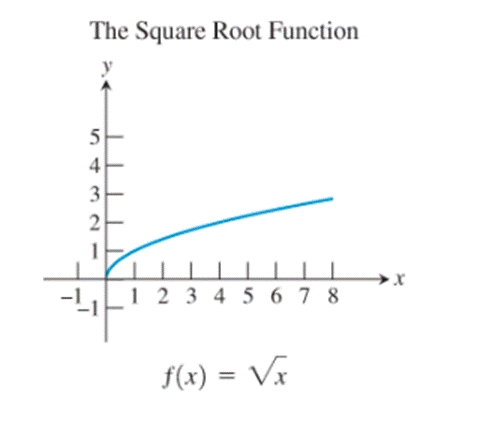
6)

  

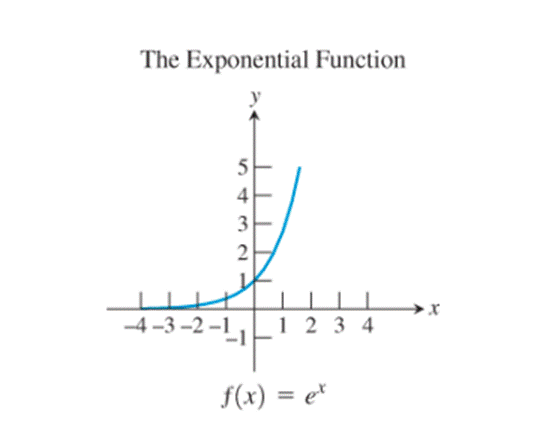
7)

  

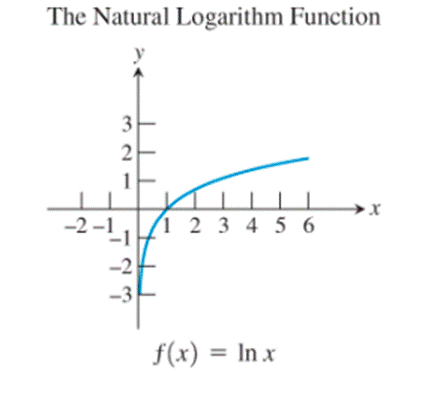
8)

  

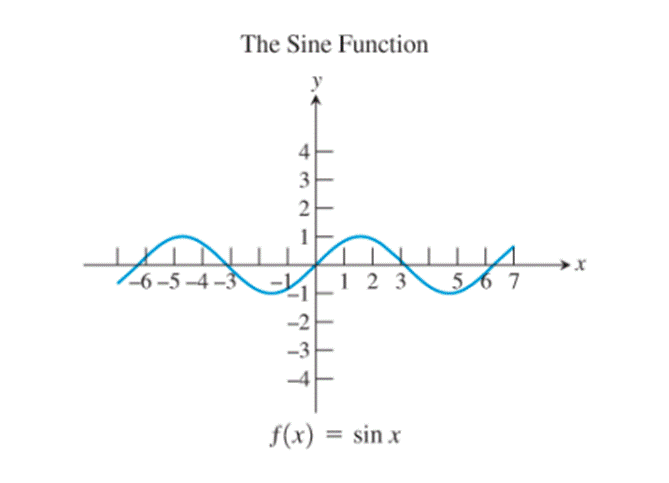
9)

  

10)

  

11)

  

12)

  

Calculation:

Any function $f$ having the property $f\left(0\right)=0$ will have its graph passing through the origin.

Now, observe the graphs of the basic functions:

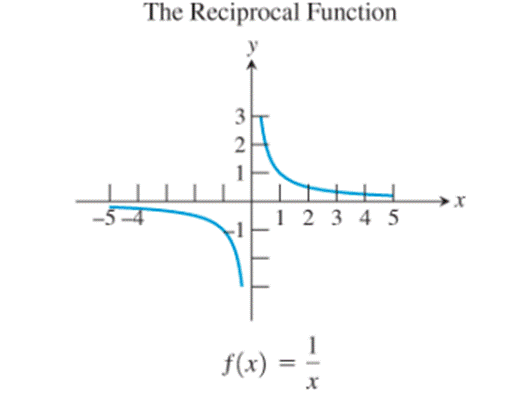
The graphs of the reciprocal function, the exponential function, the natural logarithm function, the cosine function and the logistic function seem to be not passing through the origin.

Thus, the basic functions that do not process the property that $f\left(0\right)=0$:

• The reciprocal function,
• The exponential function,
• The natural logarithm function,
• The cosine function
• The logistic function

Conclusion:

The basic functions that do not possess the property that $f\left(0\right)=0$:

• The reciprocal function,
• The exponential function,
• The natural logarithm function,
• The cosine function
• The logistic function

b.

To determine which one among the basic functions possesses the property that $f\left(x+y\right)=f\left(x\right)+f\left(y\right)$ for any $x$ and $y$ .

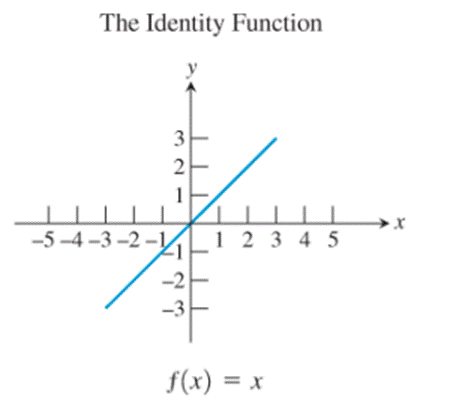
The identity function $f\left(x\right)=x$ is the one possessing the property that $f\left(x+y\right)=f\left(x\right)+f\left(y\right)$ for any $x$ and $y$ .

Given:

It is given that only one basic function possesses the property that $f\left(x+y\right)=f\left(x\right)+f\left(y\right)$ for any $x$ and $y$ .

Calculation:

Observe the identity function $f\left(x\right)=x$ :

  $\begin{array}{l}f\left(x+y\right)=x+y\\ f\left(x+y\right)=f\left(x\right)+f\left(y\right)\end{array}$ .

Thus, the identity function possesses the property.

Since it is given that only one among the basic functions possesses this property, only the identity function possesses this property.

Conclusion:

The identity function $f\left(x\right)=x$ is the one possessing the property that $f\left(x+y\right)=f\left(x\right)+f\left(y\right)$ for any $x$ and $y$ .

c.

To determine which one among the basic functions possesses the property that $f\left(x+y\right)=f\left(x\right)f\left(y\right)$ for any $x$ and $y$ .

The exponential function $f\left(x\right)=e^x$ is the one possessing the property that $f\left(x+y\right)=f\left(x\right)f\left(y\right)$ for any $x$ and $y$ .

Given:

It is given that only one basic function possesses the property that $f\left(x+y\right)=f\left(x\right)f\left(y\right)$ for any $x$ and $y$ .

Calculation:

Observe the exponential function $f\left(x\right)=e^x$ :

  $\begin{array}{l}f\left(x+y\right)=e^{x+y}\\ f\left(x+y\right)=e^x{e}^y\\ f\left(x+y\right)=f\left(x\right)f\left(y\right)\end{array}$ .

Thus, the exponential function possesses the property.

Since it is given that only one among the basic functions possesses this property, only the exponential function possesses this property.

Conclusion:

The exponential function $f\left(x\right)=e^x$ is the one possessing the property that $f\left(x+y\right)=f\left(x\right)f\left(y\right)$ for any $x$ and $y$ .

d.

To determine which one among the basic functions possesses the property that $f\left(xy\right)=f\left(x\right)+f\left(y\right)$ for any $x$ and $y$ .

The logarithmic function $f\left(x\right)=\log \left(x\right)$ is the one possessing the property that $f\left(xy\right)=f\left(x\right)+f\left(y\right)$ for any $x$ and $y$ .

Given:

It is given that only one basic function possesses the property that $f\left(xy\right)=f\left(x\right)+f\left(y\right)$ for any $x$ and $y$ .

Calculation:

Observe the logarithmic function $f\left(x\right)=\log \left(x\right)$ :

  $\begin{array}{l}f\left(xy\right)=\log \left(xy\right)\\ f\left(xy\right)=\log \left(x\right)+\log \left(y\right)\\ f\left(xy\right)=f\left(x\right)+f\left(y\right)\end{array}$ .

Thus, the logarithmic function possesses the property.

Since it is given that only one among the basic functions possesses this property, only the logarithmic function possesses this property.

Conclusion:

The logarithmic function $f\left(x\right)=\log \left(x\right)$ is the one possessing the property that $f\left(xy\right)=f\left(x\right)+f\left(y\right)$ for any $x$ and $y$ .

e.

To determine which four among the basic functions possess the property that $f\left(x\right)+f\left(-x\right)=0$ for every $x$ .

The basic functions possessing the property that $f\left(x\right)+f\left(-x\right)=0$ for very $x$ in its domain:

• The identity function
• The cubing function
• The reciprocal function
• The sine function

Given:

Given that four among the basic function possess the property that $f\left(x\right)+f\left(-x\right)=0$ for every $x$ .

Concept Used:

Any function showing the property that $f\left(x\right)+f\left(-x\right)=0$ for every $x$ in its domain is defined to be an odd function.

Now, if a function is odd, its graph will be symmetrical about the origin.

Calculation:

Observe the graphs of the basic functions:

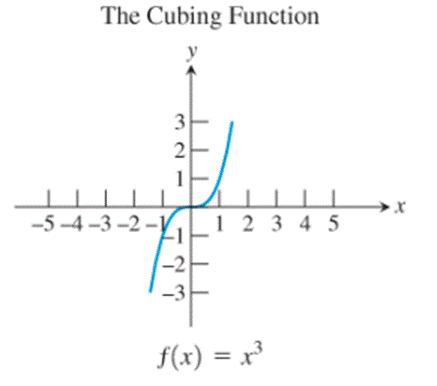
The identity function, the cubing function, the reciprocal function and the sine function are the only ones whose graphs are symmetric about the origin.

Thus, the basic functions possessing the property that $f\left(x\right)+f\left(-x\right)=0$ for very $x$ in its domain:

• The identity function
• The cubing function
• The reciprocal function
• The sine function

Conclusion:

The basic functions possessing the property that $f\left(x\right)+f\left(-x\right)=0$ for very $x$ in its domain:

• The identity function
• The cubing function
• The reciprocal function
• The sine function