
a.
To determine which of the twelve basic functions are inverses of each other.
The exponential function and the logarithmic function are the basic functions which are inverses of each other.
Concept Used:
The twelve basic functions:
1)
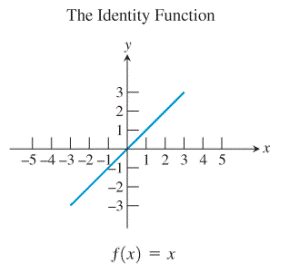
2)
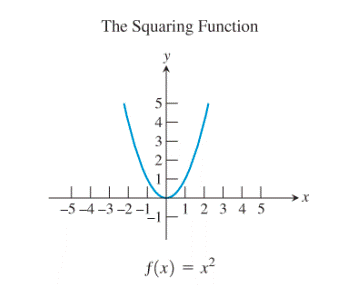
3)
4)
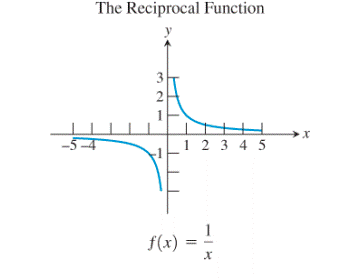
5)
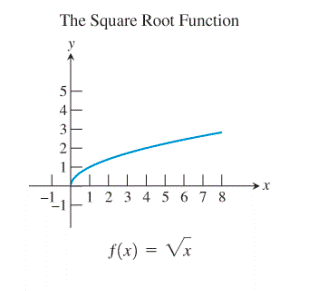
6)
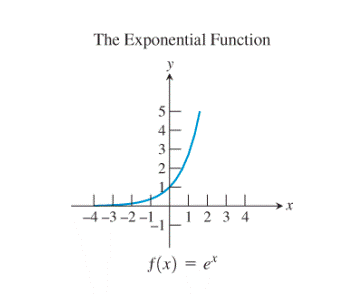
7)
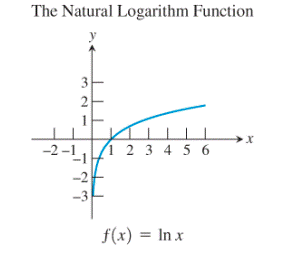
8)
9)
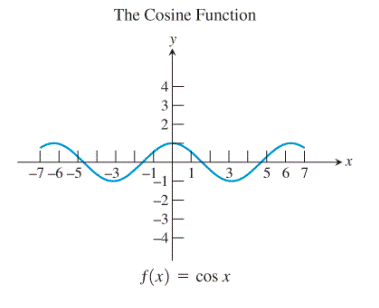
10)
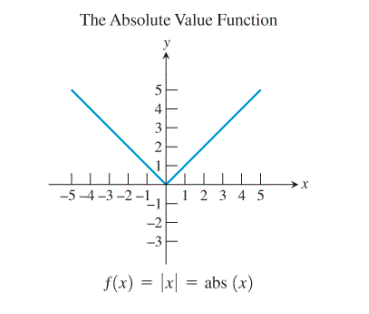
11)
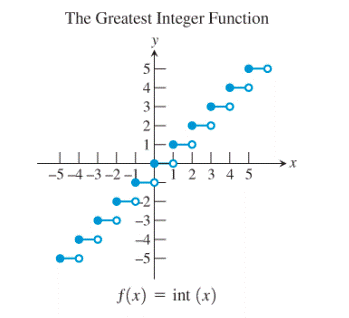
12)
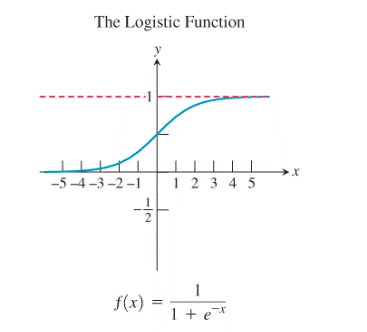
Calculation:
Observe the natural logarithm function and the exponential function:
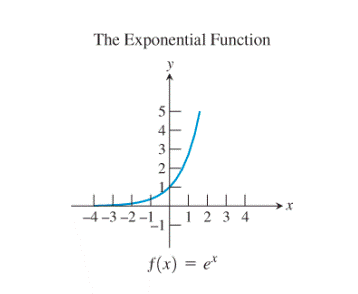
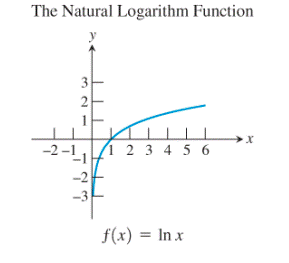
The graph of the exponential function seems to be the reflection of the logarithmic function about
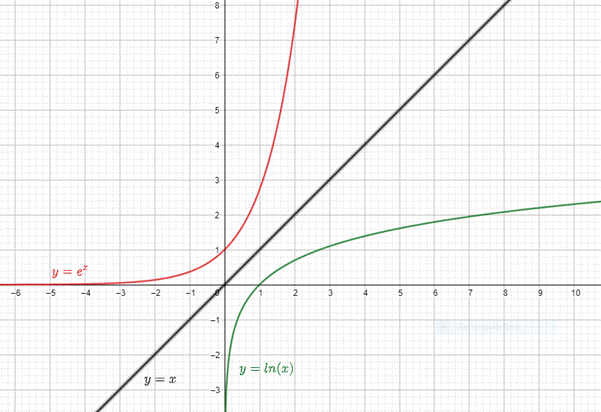
Thus, the exponential function and the logarithmic function are the basic functions which are inverses of each other. Also, no any other pair of functions seems to be showing this kind of relationship.
Conclusion:
The exponential function and the logarithmic function are the basic functions which are inverses of each other.
b.
To determine which among the basic functions are inverses of their own.
The identity function and the reciprocal function are the basic functions which are the inverses of their own.
Calculation:
Consider the identity function along with its graph:
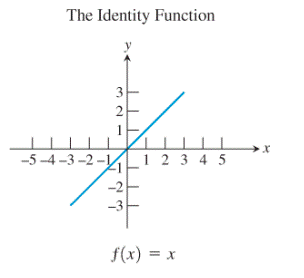
The graph is that of the line
Then, reflecting the graph of the identity function about the line
Thus, the identity function is the inverse of itself.
Now, consider the reciprocal function:
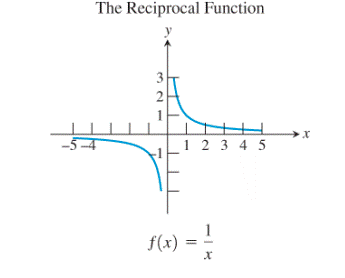
The graph of the function remains unchanged even after reflecting it about the line
Thus, the reciprocal function is also the inverse of itself.
No any other functions seem to show this property.
Thus, the identity function and the reciprocal function are the basic functions which are inverses of their own.
Conclusion:
The identity function and the reciprocal function are the basic functions which are the inverses of their own.
c.
To determine the basic function which is the inverse of another basic function when its domain is restricted to
Calculation:
Consider the squaring function:
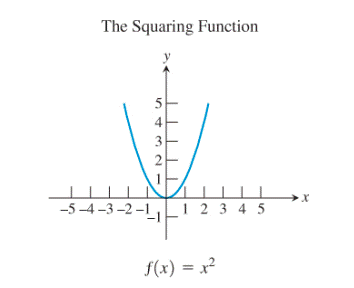
Restrict the domain of the squaring function to
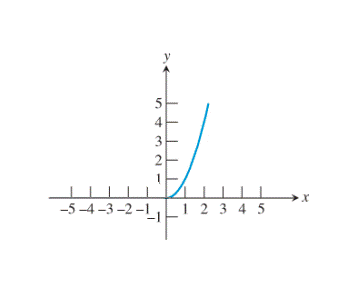
Now, reflect the graph so obtained about the line
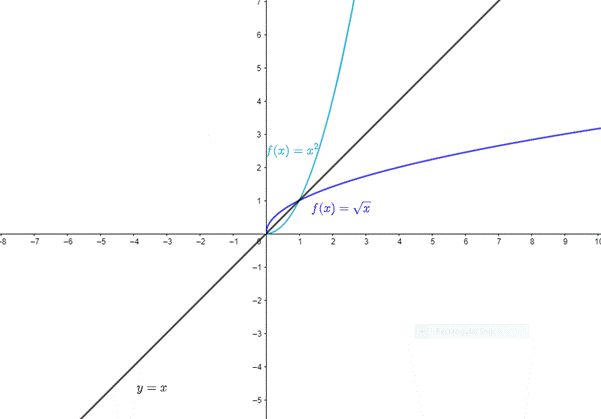
Thus, the restricted squaring function gives the square root function when it is reflected about the line
Thus, the basic function which gives the inverse of another basic function when its domain is restricted to
Conclusion:
The basic function which gives the inverse of another basic function when its domain is restricted to
Chapter 1 Solutions
PRECALCULUS:GRAPH...-NASTA ED.(FLORIDA)
- Which sign makes the statement true? 9.4 × 102 9.4 × 101arrow_forwardDO these math problems without ai, show the solutions as well. and how you solved it. and could you do it with in the time spandarrow_forwardThe Cartesian coordinates of a point are given. (a) (-8, 8) (i) Find polar coordinates (r, 0) of the point, where r > 0 and 0 ≤ 0 0 and 0 ≤ 0 < 2π. (1, 0) = (r. = ([ (ii) Find polar coordinates (r, 8) of the point, where r < 0 and 0 ≤ 0 < 2π. (5, 6) = =([arrow_forward
- The Cartesian coordinates of a point are given. (a) (4,-4) (i) Find polar coordinates (r, e) of the point, where r > 0 and 0 0 and 0 < 0 < 2π. (r, 6) = X 7 (ii) Find polar coordinates (r, 8) of the point, where r < 0 and 0 0 < 2π. (r, 0) = Xarrow_forwardr>0 (r, 0) = T 0 and one with r 0 2 (c) (9,-17) 3 (r, 8) (r, 8) r> 0 r<0 (r, 0) = (r, 8) = X X X x x Warrow_forward74. Geometry of implicit differentiation Suppose x and y are related 0. Interpret the solution of this equa- by the equation F(x, y) = tion as the set of points (x, y) that lie on the intersection of the F(x, y) with the xy-plane (z = 0). surface Z = a. Make a sketch of a surface and its intersection with the xy-plane. Give a geometric interpretation of the result that dy dx = Fx F χ y b. Explain geometrically what happens at points where F = 0. yarrow_forward
- Example 3.2. Solve the following boundary value problem by ADM (Adomian decomposition) method with the boundary conditions მი მი z- = 2x²+3 дг Əz w(x, 0) = x² - 3x, θω (x, 0) = i(2x+3). ayarrow_forward6. A particle moves according to a law of motion s(t) = t3-12t2 + 36t, where t is measured in seconds and s is in feet. (a) What is the velocity at time t? (b) What is the velocity after 3 s? (c) When is the particle at rest? (d) When is the particle moving in the positive direction? (e) What is the acceleration at time t? (f) What is the acceleration after 3 s?arrow_forwardConstruct a table and find the indicated limit. √√x+2 If h(x) = then find lim h(x). X-8 X-8 Complete the table below. X 7.9 h(x) 7.99 7.999 8.001 8.01 8.1 (Type integers or decimals rounded to four decimal places as needed.)arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





