
When the rope is at an angle of α = 30°, the 1-lb sphere A has a speed v0 = 4 ft/s. The coefficient of restitution between A and the 2-lb wedge B is 0.7 and the length of rope l = 2.6 ft. The spring constant has a value of 2 lb/in. and θ = 20°. Determine (a) the velocities of A and B immediately after the impact, (b) the maximum deflection of the spring, assuming A does not strike B again before this point.
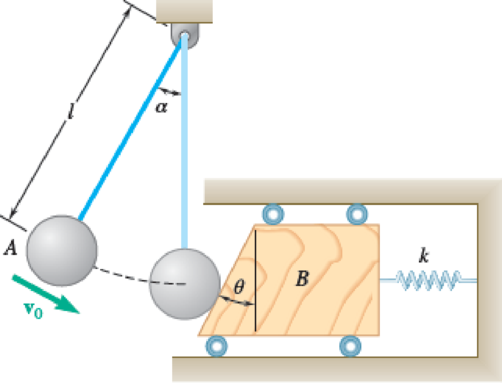
(a)
Find the velocity of A
Answer to Problem 13.188P
The velocity of A
Explanation of Solution
Given information:
The angle of the rope
The weight of the sphere A
The weight of the wedge B
The speed of the sphere A
The coefficient of restitution between A and wedge (e) is 0.7.
The length of the rope (l) is
The spring constant (k) is
The angle
The acceleration due to gravity (g) is
Calculation:
Calculate the mass of sphere A
Substitute
Calculate the mass of wedge B
Substitute
Calculate the initial altitude of sphere
Substitute
Calculate the initial potential energy of sphere
Substitute
Calculate the initial kinetic energy of sphere
Here,
Substitute
Calculate the altitude of sphere just before impact
Substitute
Calculate the initial potential energy of sphere just before impact
Substitute
Calculate the kinetic energy of sphere just before impact
Here,
Substitute
The expression for the principle of conservation of energy between initial and final stage of sphere as follows:
Substitute
Show the impulse-momentum diagram for sphere as in Figure (1).
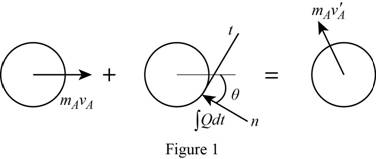
The expression for the momentum in tangential direction as follows:
Here,
Substitute
Show the impulse-momentum diagram of wedge as in Figure (2).
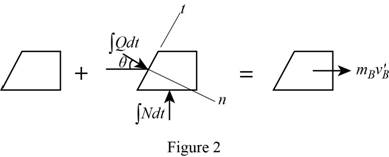
The expression for the momentum in x-direction as follows:
Here,
Substitute
Calculate the coefficient of restitution (e) using the formula:
Substitute 0.7 for e,
Find the velocity of sphere B immediately after the impact:
Substitute
Find the normal component of velocity of sphere:
Substitute
Calculate the resultant velocity of sphere A
Substitute
Calculate the angle for
Substitute
Calculate the resultant angle of velocity of sphere A
Substitute 63.77 for
Therefore, the velocity of A
(b)
Find the maximum deflection of the spring assuming A does not strike B again before this point.
Answer to Problem 13.188P
The maximum deflection of the spring
Explanation of Solution
Given information:
The angle of the rope
The weight of the sphere A
The weight of the wedge B
The speed of the sphere A
The coefficient of restitution between A and wedge (e) is 0.7.
The length of the rope (l) is
The spring constant (k) is
The angle
The acceleration due to gravity (g) is
Calculation:
Calculate the kinetic energy of wedge block just before impact
Here,
Substitute
The expression for the potential energy of spring at the end of impact
The expression for the principle of conservation of energy for wedge block as follows:
Here,
Substitute
Substitute
Therefore, the maximum deflection of the spring
Want to see more full solutions like this?
Chapter 13 Solutions
Vector Mechanics for Engineers: Statics and Dynamics
- The plate is moving at 0.6 mm/s when the force applied to the plate is 4mN. If the surface area of the plate in contact with the liquid is 0.5 m^2, deterimine the approximate viscosity of the liquid, assuming that the velocity distribution is linear.arrow_forward3-9. Given that the force acting on a particle has the following components: Fx = −x + y, Fy = x − y + y², F₂ = 0. Solve for the potential energy V. -arrow_forward2.5 (B). A steel rod of cross-sectional area 600 mm² and a coaxial copper tube of cross-sectional area 1000 mm² are firmly attached at their ends to form a compound bar. Determine the stress in the steel and in the copper when the temperature of the bar is raised by 80°C and an axial tensile force of 60 kN is applied. For steel, E = 200 GN/m² with x = 11 x 10-6 per °C. E = 100 GN/m² with α = 16.5 × 10-6 For copper, per °C. [E.I.E.] [94.6, 3.3 MN/m².]arrow_forward
- 3–16. A particle of mass m is embedded at a distance R from the center of a massless circular disk of radius R which can roll without slipping on the inside surface of a fixed circular cylinder of radius 3R. The disk is released with zero velocity from the position shown and rolls because of gravity, all motion taking place in the same vertical plane. Find: (a) the maximum velocity of the particle during the resulting motion; (b) the reaction force acting on the disk at the point of contact when it is at its lowest position. KAR 60° 3R M Fig. P3-16arrow_forwardI have figured out the support reactions, Ay = 240 kN, Ax = 0 kN, Ma = 639.2 kN*m and the constant term for V(x) is 240. I am not figuring out the function of x part right. Show how to derive V(x) and M(x) for this distributed load.arrow_forward2.4 (A). A 75 mm diameter compound bar is constructed by shrinking a circular brass bush onto the outside of a 50 mm diameter solid steel rod. If the compound bar is then subjected to an axial compressive load of 160 kN determine the load carried by the steel rod and the brass bush and the compressive stress set up in each material. For steel, E 210 GN/m²; for brass, E = 100 GN/m². [I. Struct. E.] [100.3, 59.7 kN; 51.1, 24.3 MN/m².]arrow_forward
- 1.7 (A). A bar ABCD consists of three sections: AB is 25 mm square and 50 mm long, BC is of 20 mm diameter and 40 mm long and CD is of 12 mm diameter and 50 mm long. Determine the stress set up in each section of the bar when it is subjected to an axial tensile load of 20 kN. What will be the total extension of the bar under this load? For the bar material, E = 210GN/m2. [32,63.7, 176.8 MN/mZ, 0.062mrn.l 10:41 مarrow_forward2.2 (A). If the maximum stress allowed in the copper of the cable of problem 2.1 is 60 MN/m2, determine the maximum tension which C3.75 kN.1 10:41 مarrow_forward1.1 (A). A 25mm squarecross-section bar of length 300mm carries an axial compressive load of 50kN. Determine the stress set up ip the bar and its change of length when the load is applied. For the bar material E = 200 GN/m2. [80 MN/m2; 0.12mm.larrow_forward
- 2.1 (A). A power transmission cable consists of ten copper wires each of 1.6 mm diameter surrounding three steel wires each of 3 mm diameter. Determine the combined E for the compound cable and hence determine the extension of a 30 m length of the cable when it is being laid with a tension of 2 kN. For steel, E200 GN/mZ; for copper, E = 100 GN/mZ. C151.3 GN/mZ; 9.6 mm.] 10:41 مarrow_forwardquestion 662 thank youarrow_forward1.5 (A). A simple turnbuckle arrangement is constructed from a 40 mm outside diameter tube threaded internally at each end to take two rods of 25 mm outside diameter with threaded ends. What will be the nominal stresses set up in the tube and the rods, ignoring thread depth, when the turnbuckle cames an axial load of 30 kN? Assuming a sufficient strength of thread, what maximum load can be transmitted by the turnbuckle if the maximum stress is limited to 180 MN/mz? C39.2, 61.1 MN/m2, 88.4 kN.1arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





