
To prove: The segments joining the midpoints of consecutive sides of a rectangle form a rhombus.
Explanation of Solution
Proof:
Consider rectangle OABC. The mid-points of side OA, AB, BC and CO are P, Q, R and S respectively.
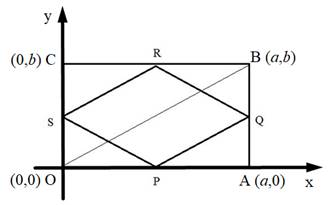
In the given figure,
By the midpoint formula, the coordinates of point P is:
By the midpoint formula, the coordinates of point Q is:
The length of PQ can be calculated by the distance formula as:
By the midpoint formula, the coordinates of point R is:
By the midpoint formula, the coordinates of point S is:
The length of SR can be calculated by the distance formula as:
Thus,
The length of PS can be calculated by the distance formula as:
It can be observed that the adjacent sides PQ and PS are equal. As PQRS is a parallelogram with adjacent sides of equal length. So, PQRS is a rhombus.
Hence, the segments joining the midpoints of consecutive sides of a rectangle form a rhombus.
Chapter 13 Solutions
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Additional Math Textbook Solutions
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Thinking Mathematically (6th Edition)
Calculus: Early Transcendentals (2nd Edition)
Elementary Statistics
A First Course in Probability (10th Edition)
Pre-Algebra Student Edition
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

