
To prove: The median of a trapezoid is parallel to each base.
Explanation of Solution
Given information: A quadrilateral is trapezoid and its median.
Proof:
Consider a trapezoid OABC with the coordinates as shown below.
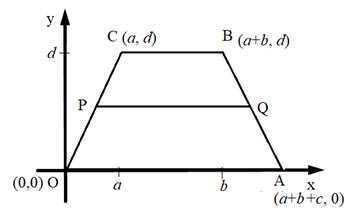
It is known that the two sides of trapezoid are parallel and two sides are nonparallel. Form the figure it can be seen that OA is parallel to CB.
Also, P is the midpoint of OC and Q is the midpoint of AB.
By the midpoint formula, the coordinates of point P are:
By the midpoint formula, the coordinates of point Q are:
As the line OA is on x -axis, so its slope is zero. Since,
Now, calculate the slope of PQ as:
As the slope of OA, CB and PQ are the same and zero, so the median PQ is parallel to each base of the trapezoid.
Hence, median of a trapezoid is parallel to each base is proved.
Chapter 13 Solutions
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Additional Math Textbook Solutions
Introductory Statistics
Thinking Mathematically (6th Edition)
Algebra and Trigonometry (6th Edition)
Calculus: Early Transcendentals (2nd Edition)
University Calculus: Early Transcendentals (4th Edition)
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

