7th Edition

ISBN: 9780470501979

Author: Frank P. Incropera, David P. DeWitt, Theodore L. Bergman, Adrienne S. Lavine

Publisher: Wiley, John & Sons, Incorporated

See similar textbooks

Videos

Textbook Question

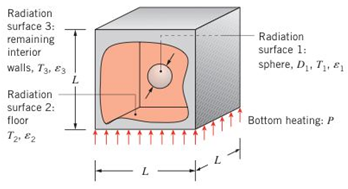
Chapter 13, Problem 13.93P

A small oven consists of a cubical box of dimension L = 0.1 m , as shown. The floor of the box consists of a heater that supplies P = 400 W . The remaining walls lose heat to the surroundings outside the oven. which maintains their temperatures at T 3 = 400 K . A spherical object of diameter D = 30 mm is placed at the center of the oven. Sometime after the sphere is placed in the oven, its temperature is T 1 = 420 K . All surfaces have emissivities of 0.4.

Chapter 13, Problem 13.93P, A small oven consists of a cubical box of dimension L=0.1m , as shown. The floor of the box consists
(a) Find the following view factors: F₁₂, F₁₃, F₂₁, F₃₁, F₂₃, F₃₂, F₃₃.
(b) Determine the temperature of the floor and the net rate of heat transfer leaving the sphere due to radiation. Is the sphere under steady-state conditions?

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter 13, Problem 13.91P

Chapter 13, Problem 13.94P

Students have asked these similar questions

100 As a spring is heated, its spring constant decreases. Suppose the spring is heated and then cooled so that the spring constant at time t is k(t) = t sin + N/m. If the mass-spring system has mass m = 2 kg and a damping constant b = 1 N-sec/m with initial conditions x(0) = 6 m and x'(0) = -5 m/sec and it is subjected to the harmonic external force f (t) = 100 cos 3t N. Find at least the first four nonzero terms in a power series expansion about t = 0, i.e. Maclaurin series expansion, for the displacement: • Analytically (hand calculations) Creating Simulink Model Plot solutions for first two, three and four non-zero terms as well as the Simulink solution on the same graph for the first 15 sec. The graph must be fully formatted by code.

Two springs and two masses are attached in a straight vertical line as shown in Figure Q3. The system is set in motion by holding the mass m₂ at its equilibrium position and pushing the mass m₁ downwards of its equilibrium position a distance 2 m and then releasing both masses. if m₁ = m² = 1 kg, k₁ = 3 N/m and k₂ = 2 N/m. (y₁ = 0) www k₁ = 3 Jm₁ = 1 k2=2 www (Net change in spring length =32-31) (y₂ = 0) m₂ = 1 32 32 System in static equilibrium System in motion Figure Q3 - Coupled mass-spring system Determine the equations of motion y₁ (t) and y₂(t) for the two masses m₁ and m₂ respectively: Analytically (hand calculations) Using MATLAB Numerical Functions (ode45) Creating Simulink Model Produce an animation of the system for all solutions for the first minute.

Two large tanks, each holding 100 L of liquid, are interconnected by pipes, with the liquid flowing from tank A into tank B at a rate of 3 L/min and from B into A at a rate of 1 L/min (see Figure Q1). The liquid inside each tank is kept well stirred. A brine solution with a concentration of 0.2 kg/L of salt flows into tank A at a rate of 6 L/min. The diluted solution flows out of the system from tank A at 4 L/min and from tank B at 2 L/min. If, initially, tank A contains pure water and tank B contains 20 kg of salt. A 6 L/min 0.2 kg/L x(t) 100 L 4 L/min x(0) = 0 kg 3 L/min 1 L/min B y(t) 100 L y(0) = 20 kg 2 L/min Figure Q1 - Mixing problem for interconnected tanks Determine the mass of salt in each tank at time t≥ 0: Analytically (hand calculations) Using MATLAB Numerical Functions (ode45) Creating Simulink Model Plot all solutions on the same graph for the first 15 min. The graph must be fully formatted by code.

Chapter 13 Solutions

Fundamentals of Heat and Mass Transfer

Ch. 13 - Determine F12 and F21 for the following...Ch. 13 - Drive expressions for the view factor F12...Ch. 13 - A right-circular cone and a right-circular...Ch. 13 - Consider the two parallel, coaxial, ringshaped...Ch. 13 - The “crossed-strings” method of Hottel [13]...Ch. 13 - Consider the rightcircular cylinder of diameter D,...Ch. 13 - Consider the parallel rectangles shown...Ch. 13 - Consider the perpendicular rectangles shown...Ch. 13 - The reciprocity relation, the summation rule, and...Ch. 13 - Determine the shape factor, F12, for the...

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.

Solution Summary: The author calculates the view factor using the reciprocity. The length of the surface is L=0.1m.

Videos

Want to see the full answer?

Chapter 13 Solutions