Fundamentals of Heat and Mass Transfer
7th Edition
ISBN: 9780470501979
Author: Frank P. Incropera, David P. DeWitt, Theodore L. Bergman, Adrienne S. Lavine
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 13, Problem 13.70P
A molten aluminum alloy at 900 K is poured into a cylindrical container that is well insulated from large surroundings at 300 K. The inner diameter of the container is 250 mm, and the distance from the surface of the melt to the top of the container is 100 mm.
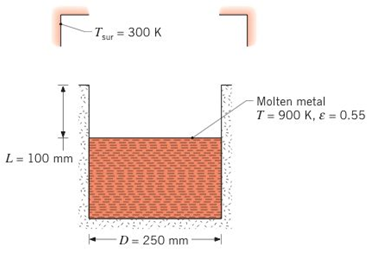
If the oxidized aluminum at the surface of the melt has an emissivity of 0.55, what is the net rate of radiation heat transfer from the melt?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Need help
Y
F1
α
В
X
F2
You and your friends are planning to move the log. The log.
needs to be moved straight in the x-axis direction and it
takes a combined force of 2.9 kN. You (F1) are able to exert
610 N at a = 32°. What magnitude (F2) and direction (B) do
you needs your friends to pull?
Your friends had to pull at:
magnitude in Newton, F2
=
direction in degrees, ẞ =
N
deg
Problem 1
8 in.
in.
PROBLEM 15.109
Knowing that at the instant shown crank BC has a constant angular
velocity of 45 rpm clockwise, determine the acceleration (a) of Point A,
(b) of Point D.
8 in.
Answer: convert rpm to rad/sec first. (a). -51.2j in/s²; (b). 176.6 i + 50.8 j in/s²
Chapter 13 Solutions
Fundamentals of Heat and Mass Transfer
Ch. 13 - Determine F12 and F21 for the following...Ch. 13 - Drive expressions for the view factor F12...Ch. 13 - A right-circular cone and a right-circular...Ch. 13 - Consider the two parallel, coaxial, ringshaped...Ch. 13 - The “crossed-strings” method of Hottel [13]...Ch. 13 - Consider the rightcircular cylinder of diameter D,...Ch. 13 - Consider the parallel rectangles shown...Ch. 13 - Consider the perpendicular rectangles shown...Ch. 13 - The reciprocity relation, the summation rule, and...Ch. 13 - Determine the shape factor, F12, for the...
Ch. 13 - Consider parallel planes of infinite extent normal...Ch. 13 - Consider the parallel planes of infinite extent...Ch. 13 - Consider two diffuse surfaces A1 and A2 on the...Ch. 13 - As shown in the sketch, consider the disk A1...Ch. 13 - A heat flux gage of 4mm diameter is positioned...Ch. 13 - A circular ice rink 25 m in diameter is enclosed...Ch. 13 - A drying oven consists of a long semicircular duct...Ch. 13 - Consider the arrangement of the three black...Ch. 13 - A long, Vshaped pan is heat treated by suspending...Ch. 13 - Consider coaxial, parallel, black disks separated...Ch. 13 - A tubular healer with a black inner surface of...Ch. 13 - A circular plate of 500-mm diameter is maintained...Ch. 13 - To enhance heat rejection from a spacecraft, an...Ch. 13 - Determine the temperatures of surfaces 1 through 4...Ch. 13 - A cylindrical cavity of diameter D and depth L is...Ch. 13 - In the arrangement shown, the tower disk has a...Ch. 13 - Two plane coaxial disks are separated by a...Ch. 13 - A radiometer views a small target (1) that is...Ch. 13 - A meter to measure the power of a laser beam is...Ch. 13 - The arrangement shown is to be used to calibrate a...Ch. 13 - A long, cylindrical heating element of 20-mm...Ch. 13 - Water flowing through a large number of long,...Ch. 13 - A row of regularly spaced, cylindrical heating...Ch. 13 - A manufacturing process calls for heating long...Ch. 13 - Consider the very long, inclined black surfaces...Ch. 13 - Many products are processed in a manner that...Ch. 13 - Consider two very large parallel plates with...Ch. 13 - A flat-bottomed hole 6 mm in diameter is bored to...Ch. 13 - In Problems 12.20 and 12.25, we estimated the...Ch. 13 - Consider the cavities formed by a cone, cylinder,...Ch. 13 - Consider the attic of a home located in a hot...Ch. 13 - A long, thin-walled horizontal tube 100 mm in...Ch. 13 - A t=5-mm -thick sheet of anodized aluminum is used...Ch. 13 - Consider the spacecraft heat rejection scheme of...Ch. 13 - A very long electrical conductor 10 mm in diameter...Ch. 13 - Liquid oxygen is stored in a thin-walled,...Ch. 13 - Two concentric spheres of diameter D1=0.8m and...Ch. 13 - Determine the steady-stale temperatures of two...Ch. 13 - Consider two large (infinite) parallel planes that...Ch. 13 - Consider two large, diffuse, gray, parallel...Ch. 13 - Heat transfer by radiation occurs between two...Ch. 13 - The end of a cylindrical liquid cryogenic...Ch. 13 - At the bottom of a very large vacuum chamber whose...Ch. 13 - A furnace is located next to a dense array of...Ch. 13 - A cryogenic fluid flows through a tube 20 mm in...Ch. 13 - A diffuse, gray radiation shield of 60mm diameter...Ch. 13 - Consider the three-surface enclosure shown. The...Ch. 13 - Two parallel, aligned disks, 0.4 m in diameter and...Ch. 13 - Coatings applied to long metallic strips are cured...Ch. 13 - A molten aluminum alloy at 900 K is poured into a...Ch. 13 - A long, hemicylindrical (1-m radius) shaped...Ch. 13 - The bottom of a steam-producing still of 200-mm...Ch. 13 - A long cylindrical healer element of diameter...Ch. 13 - A radiative heater consists of a bank of ceramic...Ch. 13 - Consider a long duct constructed with diffuse,...Ch. 13 - A solar collector consists of a long duct through...Ch. 13 - The cylindrical peephole in a furnace wall of...Ch. 13 - A composite wall is comprised of two large plates...Ch. 13 - A small disk of diameter D1=50mm and emissivity...Ch. 13 - Consider a cylindrical cavity of diameter D=100mm...Ch. 13 - Consider a circular furnace that is 0.3 m long and...Ch. 13 - Consider two very large metal parallel plates. The...Ch. 13 - Two convex objects are inside a large vacuum...Ch. 13 - the diffuse, gray, four-surface enclosure with all...Ch. 13 - A cylindrical furnace for heal-treating materials...Ch. 13 - A laboratory oven bas a cubical interior chamber 1...Ch. 13 - A small oven consists of a cubical box of...Ch. 13 - An opaque, diffuse, gray (200mm200mm) plate with...Ch. 13 - A tool for processing silicon waters is housed...Ch. 13 - Consider Problem 6.17. The stationary plate,...Ch. 13 - Most architects know that the ailing of an...Ch. 13 - Boiler tubes exposed to the products of coal...Ch. 13 - Consider two very large parallel plates. The...Ch. 13 - Coated metallic disks are cured by placing them at...Ch. 13 - A double-glazed window consists of two panes of...Ch. 13 - Electrical conductors, in the form of parallel...Ch. 13 - The spectral absorptivity of a large diffuse...Ch. 13 - The cross section of a long circular tube, which...Ch. 13 - Cylindrical pillars similar to those of Problem...Ch. 13 - A row of regularly spaced, cylindrical healing...Ch. 13 - The composite insulation shown, which was...Ch. 13 - Hot coffee is contained in a cylindrical thermos...Ch. 13 - Consider a vertical, double-pane window for the...Ch. 13 - Consider the double-pane window of Problem 9.95,...Ch. 13 - A flat-plate solar collector, consisting of an...Ch. 13 - Consider the tube and radiation shield of Problem...Ch. 13 - Consider the tube and radiation shield of Problem...Ch. 13 - Consider the flatplate solar collector of Problem...Ch. 13 - The lower side of a 400-mm-diameter disk is heated...Ch. 13 - The surface of a radiation shield facing a black...Ch. 13 - The fire tube of a hot water heater consists of a...Ch. 13 - Consider the conditions of Problem 9.107....Ch. 13 - A special surface coating on a square panel that...Ch. 13 - A long rod heater of diameter D1=10mm and...Ch. 13 - A radiant heater, which is used for surface...Ch. 13 - A steam generator consists of an in-line array of...Ch. 13 - A furnace having a spherical cavity of 0.5-m...Ch. 13 - A gas turbine combustion chamber may be...Ch. 13 - A flue gas at 1-atm total pressure and a...Ch. 13 - A furnace consists of two large parallel plates...Ch. 13 - In an industrial process, products of combustion...Ch. 13 - A grain dryer consists of a long semicircular duct...Ch. 13 - A novel infrared recycler has been proposed for...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Problem 4 The semicircular disk has a radius of 0.4 m. At one instant, when 0-60°, it is rotating counterclockwise at 0-4 rad/s, which is increasing in the same direction at 1 rad/s². Find the velocity and acceleration of point B at this instant. (Suggestion: Set up relative velocity and relative acceleration that way you would for a no-slip disk; remember what I told you to memorize on the first day of class.) (Answer: B = −2.98î - 0.8ĵ m/s, ãB = 2.45î - 5.74ĵ m/s²) B 0.4 m y Xarrow_forwardA C C 2r A 2r B B (a) (b) Problem 3 Refer to (b) of the figure shown above. The disk OA is now rolling with no slip at a constant angular velocity of w. Find the angular velocity and angular acceleration of link AB and BC. (Partial Answers: WBC = 2wk, AB = w²k)arrow_forwardProblem 2 Refer to (a) of the figure shown below, where the disk OA rotates at a constant angular velocity of w. Find the angular velocity and angular acceleration of link AB and link BC. (Partial Answers: WBC = wk, AB = w²k) A 2r C B (a) A 2r B (b)arrow_forward
- Example Two rotating rods are connected by slider block P. The rod attached at A rotates with a constant clockwise angular velocity WA. For the given data, determine for the position shown (a) the angular velocity of the rod attached at B, (b) the relative velocity of slider block P with respect to the rod on which it slides. b = 8 in., w₁ = 6 rad/s. Given: b = 8 in., WA = 6 rad/s CW constant Find: (a). WBE (b). Vp/Frame E 60° 20° Barrow_forwardY F1 α В X F2 You and your friends are planning to move the log. The log. needs to be moved straight in the x-axis direction and it takes a combined force of 2.9 kN. You (F1) are able to exert 610 N at a = 32°. What magnitude (F2) and direction (B) do you needs your friends to pull? Your friends had to pull at: magnitude in Newton, F2 = direction in degrees, ẞ = N degarrow_forward100 As a spring is heated, its spring constant decreases. Suppose the spring is heated and then cooled so that the spring constant at time t is k(t) = t sin + N/m. If the mass-spring system has mass m = 2 kg and a damping constant b = 1 N-sec/m with initial conditions x(0) = 6 m and x'(0) = -5 m/sec and it is subjected to the harmonic external force f (t) = 100 cos 3t N. Find at least the first four nonzero terms in a power series expansion about t = 0, i.e. Maclaurin series expansion, for the displacement: • Analytically (hand calculations) Creating Simulink Model Plot solutions for first two, three and four non-zero terms as well as the Simulink solution on the same graph for the first 15 sec. The graph must be fully formatted by code.arrow_forward
- Two springs and two masses are attached in a straight vertical line as shown in Figure Q3. The system is set in motion by holding the mass m₂ at its equilibrium position and pushing the mass m₁ downwards of its equilibrium position a distance 2 m and then releasing both masses. if m₁ = m² = 1 kg, k₁ = 3 N/m and k₂ = 2 N/m. (y₁ = 0) www k₁ = 3 Jm₁ = 1 k2=2 www (Net change in spring length =32-31) (y₂ = 0) m₂ = 1 32 32 System in static equilibrium System in motion Figure Q3 - Coupled mass-spring system Determine the equations of motion y₁ (t) and y₂(t) for the two masses m₁ and m₂ respectively: Analytically (hand calculations) Using MATLAB Numerical Functions (ode45) Creating Simulink Model Produce an animation of the system for all solutions for the first minute.arrow_forwardTwo large tanks, each holding 100 L of liquid, are interconnected by pipes, with the liquid flowing from tank A into tank B at a rate of 3 L/min and from B into A at a rate of 1 L/min (see Figure Q1). The liquid inside each tank is kept well stirred. A brine solution with a concentration of 0.2 kg/L of salt flows into tank A at a rate of 6 L/min. The diluted solution flows out of the system from tank A at 4 L/min and from tank B at 2 L/min. If, initially, tank A contains pure water and tank B contains 20 kg of salt. A 6 L/min 0.2 kg/L x(t) 100 L 4 L/min x(0) = 0 kg 3 L/min 1 L/min B y(t) 100 L y(0) = 20 kg 2 L/min Figure Q1 - Mixing problem for interconnected tanks Determine the mass of salt in each tank at time t≥ 0: Analytically (hand calculations) Using MATLAB Numerical Functions (ode45) Creating Simulink Model Plot all solutions on the same graph for the first 15 min. The graph must be fully formatted by code.arrow_forward5. Estimate the friction pressure gradient in a 10.15 cm bore unheated horizontal pipe for the following conditions: Fluid-propylene Pressure 8.175 bar Temperature-7°C Mass flow of liquid-2.42 kg/s. Density of liquid-530 kg/m³ Mass flow of vapour-0.605 kg/s. Density of vapour-1.48 kg/m³arrow_forward
- Describe the following HVAC systems. a) All-air systems b) All-water systems c) Air-water systems Graphically represent each system with a sketch.arrow_forwardTwo large tanks, each holding 100 L of liquid, are interconnected by pipes, with the liquid flowing from tank A into tank B at a rate of 3 L/min and from B into A at a rate of 1 L/min (see Figure Q1). The liquid inside each tank is kept well stirred. A brine solution with a concentration of 0.2 kg/L of salt flows into tank A at a rate of 6 L/min. The diluted solution flows out of the system from tank A at 4 L/min and from tank B at 2 L/min. If, initially, tank A contains pure water and tank B contains 20 kg of salt. A 6 L/min 0.2 kg/L x(t) 100 L 4 L/min x(0) = 0 kg 3 L/min 1 L/min B y(t) 100 L y(0) = 20 kg 2 L/min Figure Q1 - Mixing problem for interconnected tanks Determine the mass of salt in each tank at time t≥ 0: Analytically (hand calculations) Using MATLAB Numerical Functions (ode45) Creating Simulink Model Plot all solutions on the same graph for the first 15 min. The graph must be fully formatted by code.arrow_forwardased on the corresponding mass flow rates (and NOT the original volumetric flow rates) determine: a) The mass flow rate of the mixed air (i.e., the combination of the two flows) leaving the chamber in kg/s. b) The temperature of the mixed air leaving the chamber. Please use PyscPro software for solving this question. Notes: For part (a), you will first need to find the density or specific volume for each state (density = 1/specific volume). The units the 'v' and 'a' are intended as subscripts: · kgv = kg_v = kgv = kilogram(s) [vapour] kga = kg_a =kga = kilogram(s) [air]arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...
Mechanical Engineering
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Cengage Learning
Heat Transfer – Conduction, Convection and Radiation; Author: NG Science;https://www.youtube.com/watch?v=Me60Ti0E_rY;License: Standard youtube license